NOIP2016提高组D1T2 天天爱跑步

n<=300000个点的树，每个点有个人于第Ti秒观测，有m<=300000个人于时间0开始从Sj跑到Tj，速度1个点每秒，输出每个点上的人观察到的跑步的人的数量。

前25分：直接模拟每条路径，先s跑到lca再跑到t，边跑边记时间，如果经过某个点时时间刚好一样就该点答案++。

Si等于1的20分：观察人能观察到，只有他观察的时间和深度相等的时候。而一个跑步人跑下来就是这条链上满足“观察时间等于深度”的点答案+1，这可以用一个差分标记解决，如下图。

这样，最后从根节点开始向下dfs，一路上把标记加上，满足“观察时间等于深度”的点的答案就是当前的标记，而其他的点答案为0。

树变成一条链的15分：这启发着我们去追寻观察人的信息和跑步人的信息的关系。若有个人从Si跑到Ti，那么观测点j能观测到的条件就是j-Si=Wj且j<=Ti。那就是找j-Wj=Si的。类似于刚才的差分标记，把一个Si->Ti记两个标记，在Si处把数组中下标Si++，在Ti+1处--，扫过来的时候，把标记处理完，再查找下标j-Wj的点有几个，就可以直接回答询问。

最后的分：其实会以上这些，再不写正解就可惜了，因为推导的过程都差不多，方法也差不多。现在来看一个路径：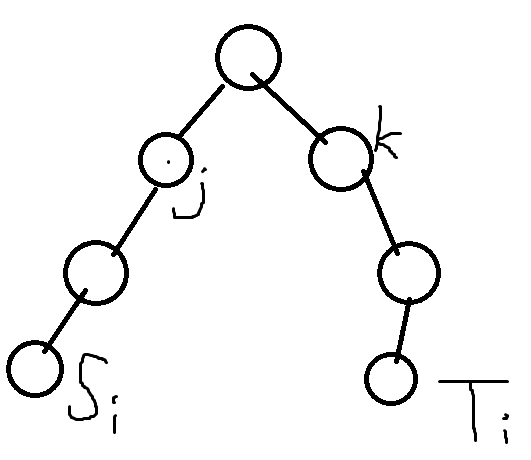

一个路径其实就一上一下两个过程，在向上经过j点时观察到的条件是：dep(Si)-dep(j)=Wj，dep()表示深度，Wj为观测时间。接下来到k那边和Si就无关了，但与之相关的Ti：dep(Ti)-dep(k)=Li-Wk，其中Li表示路径i的长度，也就是到Ti的时间，这段时间差恰好等于Ti到k的长度时可以观测到。整理两个式子，dep(Si)=dep(j)+Wj，dep(Ti)-Li=dep(k)-Wk。这么看来，回答一个询问，实际上是找这个观测点的子树里有多少个i满足上面两个式子。

不过这样是有偏差的。例如这样：

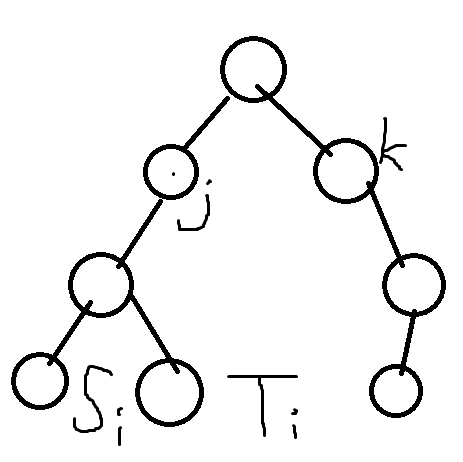
Si和Ti尽管是j的子树内的点，但他们对答案没影响。而j的孩子点，Si和Ti在这里会被计算两次。也就是要想个办法把Si和Ti能影响的范围表示出来。

可以发现，根据dfs的顺序，如果在Si处把对应信息+1，Ti处+1，那么在lca(Si,Ti)处应-1，lca的父亲那里再-1，这样一来，就可以使得Si到Ti的路径上每个点统计答案时只算到他们一次。

也就是说，开A，B两个数组存dep(j)+Wj和dep(j)-Wj两种信息，把一个跑步人拆成四个信息变化：在Si处，A数组中信息点dep(Si)加一；在Ti处，B数组中信息点dep(Ti)-Li加一；在lca(Si,Ti)处，A数组中信息点dep(Si)减一；在lca的父亲那里，B数组中信息点dep(Ti)-Li减一。信息点的变化以邻接表的形式连在它应该在的位置，在访问一棵子树时，先遍历子树，再把这个点的所有信息点变化处理好，然后在A，B两个数组中直接查对应值dep(j)+Wj，dep(j)-Wj的信息，这个信息就是答案。

具体见代码。由于B数组里的信息点涉及减法，故把B数组里的值都加上了n，查询时也加上n即可。

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #include<algorithm>
 //#include<iostream>
 using namespace std;

 int n,m;
 #define maxn 300011
 struct Edge{int to,next;}edge[maxn*];int first[maxn],le=;
 int dep[maxn],fa[maxn][];
 void in(int x,int y) {Edge &e=edge[le];e.to=y;e.next=first[x];first[x]=le++;}
 void insert(int x,int y) {in(x,y);in(y,x);}
 void dfs(int x,int f)
 {
     dep[x]=dep[f]+;fa[x][]=f;
     for (int i=first[x];i;i=edge[i].next)
     {
         const Edge &e=edge[i];
         if (e.to!=f) dfs(e.to,x);
     }
 }
 void makef()
 {
     for (int j=;j<=;j++)
         for (int i=;i<=n;i++)
             fa[i][j]=fa[fa[i][j-]][j-];
 }
 int lca(int x,int y)
 {
     if (dep[x]<dep[y]) {int t=x;x=y;y=t;}
     for (int j=;j>=;j--) if (dep[fa[x][j]]>=dep[y]) x=fa[x][j];
     if (x==y) return x;
     for (int j=;j>=;j--) if (fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j];
     return fa[x][];
 }
 struct List{bool sig,add;int v,next;}list[maxn*];int eve[maxn],ll=;
 void addeve(int x,bool sig,bool add,int v)
 {
     List &l=list[ll];l.sig=sig;l.add=add;l.v=v;
     l.next=eve[x];eve[x]=ll++;
 }
 int wa[maxn],pos[maxn*],neg[maxn*],ans[maxn];
 void play(int x,int f)
 {
     ans[x]=pos[wa[x]+dep[x]]+neg[wa[x]-dep[x]+n];
     for (int i=first[x];i;i=edge[i].next)
     {
         const Edge &e=edge[i];
         if (e.to!=f) play(e.to,x);
     }
     for (int i=eve[x];i;i=list[i].next)
     {
         const List &e=list[i];
         if (e.sig) pos[e.v]+=e.add?:-;
         else neg[e.v]+=e.add?:-;
     }
     ans[x]=pos[wa[x]+dep[x]]+neg[wa[x]-dep[x]+n]-ans[x];
 }
 int x,y;
 int main()
 {
     scanf("%d%d",&n,&m);
     memset(first,,sizeof(first));
     memset(eve,,sizeof(eve));
     for (int i=;i<n;i++)
     {
         scanf("%d%d",&x,&y);
         insert(x,y);
     }
     dfs(n/+,);makef();
     for (int i=;i<=n;i++) scanf("%d",&wa[i]);
     for (int i=;i<=m;i++)
     {
         scanf("%d%d",&x,&y);
         int l=lca(x,y),d=dep[x]+dep[y]-*dep[l];
         addeve(x,,,dep[x]);
         addeve(y,,,d-dep[y]+n);
         addeve(l,,,dep[x]);
         addeve(fa[l][],,,d-dep[y]+n);
     }
     memset(pos,,sizeof(pos));
     memset(neg,,sizeof(neg));
     play(n/+,);
     for (int i=;i<n;i++) printf("%d ",ans[i]);printf("%d",ans[n]);
     return ;
 }

自测在vijos上取n/2+3为根可以通过所有的点。