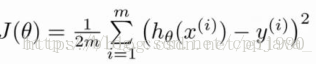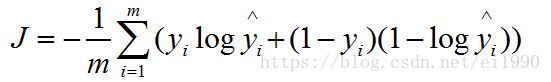机器学习(三)—线性回归、逻辑回归、Softmax回归 的区别
1、什么是回归?
是一种监督学习方式,用于预测输入变量和输出变量之间的关系,等价于函数拟合,选择一条函数曲线使其更好的拟合已知数据且更好的预测未知数据。
2、线性回归
于一个一般的线性模型而言,其目标就是要建立输入变量和输出变量之间的回归模型。该模型是既是参数的线性组合,同时也是输入变量的线性组合。

最小二乘法,代价函数(平方误差代价函数,加1/2是为了方便求导):
这里使用基函数(basis function)对上面的线性模型进行拓展,即:线性回归模型是一组输入变量x的非线性基函数的线性组合。
(相当于SVM里面的核函数— 线性核、多项式核、高斯核、sigmoid核)
梯度下降法:
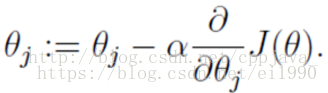
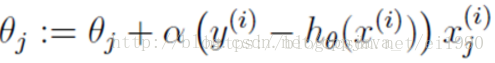
(1) 批处理梯度下降法:每次对全部训练数据进行求导后更新参数,能求得最优解;
(2) 增量梯度下降法:每扫描一个训练样本就更新参数,快,训练集很大时选择。
正规方程组求解(The normal equations):直接令代价函数对参数求导为0:
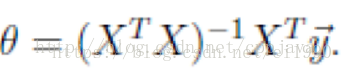
步长(学习率)的选择:过小,迭代次数非常高;过大,越过最小值无法收敛。0.01,0.03,0.1,0.3,1,3,10
特征值归一化:多维特征时,需要确保特征的取值范围在相同的尺度内计算过程才会收敛,常用方法有(1) (X- mean(X))/std(X);(2) (X - min) / (max - min)。
3、逻辑回归
目的:从训练数据特征学习出一个0/1分类模型。
预测函数:
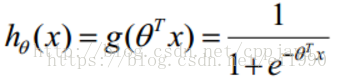
优点:计算代价不高,易于理解和实现;缺点:容易欠拟合,分类精度不高
观测值的概率:
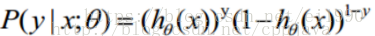
损失代价函数:
4. Softmax回归模型
当多分类问题时,logistic推广为softmax.
假设函数:
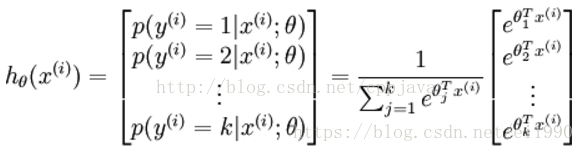
损失函数:
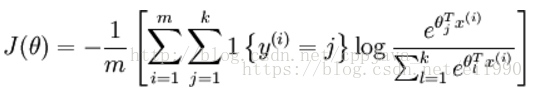
为了解决softmax回归的参数冗余带来的数值问题,可以加入权重衰减项
5. 过拟合和欠拟合如何产生,如何解决?
欠拟合:根本原因是特征维度过少,导致拟合的函数无法满足训练集,误差较大;解决方法:增加特征维度;
过拟合:根本原因是特征维度过大,导致拟合的函数完美的经过训练集,但对新数据的预测结果差。解决方法:(1)减少特征维度;(2)正则化,降低参数值。
减少过拟合总结:过拟合主要是有两个原因造成的:数据太少+模型太复杂
(1)获取更多数据 :从数据源头获取更多数据;数据增强(Data Augmentation) :数据增强,常用的方式:上下左右翻转flip,旋转图像,平移变换,随机剪切crop图像,图像尺度变换,改变图像色差、对比度,仿射变换,扭曲图像特征,增强图像噪音(一般使用高斯噪音,盐椒噪音)等
(2)使用合适的模型:减少网络的层数、神经元个数等均可以限制网络的拟合能力;
(3)dropout
(3)正则化,在训练的时候限制权值变大;
(4)限制训练时间;通过评估测试;
(4)增加噪声 Noise: 输入时+权重上(高斯初始化)
(5)结合多种模型: Bagging用不同的模型拟合不同部分的训练集;Boosting只使用简单的神经网络;
6、逻辑回归和线性回归区别
1)线性回归要求变量服从正态分布,logistic回归对变量分布没有要求。
2)线性回归要求因变量是连续性数值变量,而logistic回归要求因变量是分类型变量。
3)线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
4)因变量不同:logistic回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
Logistic Regression最大的特点就是将函数值收缩到[0,1]这个范围。
注意:能和逻辑斯蒂回归进行比较的就是牛逼闪闪的线性SVM了。大概意思是:直接用线性回归做分类因为考虑到了所有样本点到分类决策面的距离,所以在两类数据分布不均匀的时候将导致误差非常大;逻辑斯蒂回归回归和SVM克服了这个缺点,前者采用将所有数据采用sigmod函数进行了非线性映射,使得远离分类决策面的数据作用减弱;后者则直接去掉了远离分类决策面的数据,只考虑支持向量的影响。
机器学习(三)—线性回归、逻辑回归、Softmax回归 的区别的更多相关文章
- 【分类器】感知机+线性回归+逻辑斯蒂回归+softmax回归
一.感知机 详细参考:https://blog.csdn.net/wodeai1235/article/details/54755735 1.模型和图像: 2.数学定义推导和优化: 3.流程 ...
- 机器学习之线性回归---logistic回归---softmax回归
在本节中,我们介绍Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签 可以取两个以上的值. Softmax回归模型对于诸如MNIST手写数字分类等问题 ...
- Softmax回归 softMax回归与logistic回归的关系
简介 在本节中,我们介绍Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签 可以取两个以上的值. Softmax回归模型对于诸如MNIST手写数字分 ...
- 机器学习 —— 基础整理(五)线性回归;二项Logistic回归;Softmax回归及其梯度推导;广义线性模型
本文简单整理了以下内容: (一)线性回归 (二)二分类:二项Logistic回归 (三)多分类:Softmax回归 (四)广义线性模型 闲话:二项Logistic回归是我去年入门机器学习时学的第一个模 ...
- 【机器学习基础】逻辑回归——LogisticRegression
LR算法作为一种比较经典的分类算法,在实际应用和面试中经常受到青睐,虽然在理论方面不是特别复杂,但LR所牵涉的知识点还是比较多的,同时与概率生成模型.神经网络都有着一定的联系,本节就针对这一算法及其所 ...
- 机器学习——softmax回归
softmax回归 前面介绍了线性回归模型适用于输出为连续值的情景.在另一类情景中,模型输出可以是一个像图像类别这样的离散值.对于这样的离散值预测问题,我们可以使用诸如 softmax 回归在内的分类 ...
- 02-13 Softmax回归
目录 Softmax回归 一.Softmax回归详解 1.1 让步比 1.2 不同类之间的概率分布 1.3 目标函数 1.4 目标函数最大化 二.Softmax回归优缺点 2.1 优点 2.2 缺点 ...
- 利用TensorFlow识别手写的数字---基于Softmax回归
1 MNIST数据集 MNIST数据集主要由一些手写数字的图片和相应的标签组成,图片一共有10类,分别对应从0-9,共10个阿拉伯数字.原始的MNIST数据库一共包含下面4个文件,见下表. 训练图像一 ...
- Stanford大学机器学习公开课(三):局部加权回归、最小二乘的概率解释、逻辑回归、感知器算法
(一)局部加权回归 通常情况下的线性拟合不能很好地预测所有的值,因为它容易导致欠拟合(under fitting).如下图的左图.而多项式拟合能拟合所有数据,但是在预测新样本的时候又会变得很糟糕,因为 ...
随机推荐
- 解决Oracle安装时报错“SID已在使用”办法
1. 开始->设置->控制面板->管理工具->服务 停止所有Oracle服务. 2. 开始->程序->Oracle - OraHome81->Oracle I ...
- D3D9和OpenGL加载纹理图片的API是哪个?
D3D9 创建一个空纹理,当返回 S_OK 且 ppTexture 纹理对象指针不为 NULL 时,则表示该函数调用成功. HRESULT D3DXCreateTexture( _In_ LPDIR ...
- 前端框架之jQuery
一 iQuery是什么 jQuery由美国人John Resig创建,至今已吸引了来自世界各地的众多 javascript高手加入其team jQuery是继prototype之后又一个优秀的Java ...
- Laravel 出现"RuntimeException inEncrypter.php line 43: The only supported ciphers are AES-128-CBC and AES-256-CBC with the correct key lengths."问题的解决办法
如果输入命令:php artisan key:generate 还是报错 那就要从别的项目里复制一个key到.env中,然后再运行命令:composer update和php artisan key: ...
- ACM解题之回文序列
题意: 一个长度为 n 的序列 a1, m2, ..., an-1, an,如果 ai = an-i+1, i = 1, 2, ..., n,则称之为"回文序列".本题对于给定的一 ...
- Serv-u 外网访问内网的FTP服务器
1. 背景简介 最近研究如何在内网搭架FTP服务器,同时要保证外网(公网)能访问的到.终成正果,但走了一些弯路,在此记下,以飨后人. 2. 基础知识 FTP 使用 2 个端口,一个数据端口和一个命令端 ...
- SQL SERVER 2005 Express版, 精简版 下载
Microsoft SQL Server 2005 Express Edition(数据库) https://www.microsoft.com/zh-CN/download/details.as ...
- LeetCode:螺旋矩阵||【59】
LeetCode:螺旋矩阵||[59] 题目描述 给定一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵. 示例: 输入: 3 输出: [ [ 1, 2, 3 ...
- Python 4 函数的参数,内置函数,装饰器,生成器,迭代器,
一.函数的参数: 1.位置参数:调用函数时根据函数定义的参数位置来传递参数. 2.关键字参数:用于函数调用,通过“键-值”形式加以指定.可以让函数更加清晰.容易使用,同时也清除了参数的顺序需求. 3. ...
- 深入浅出Node.js(下)
(五):Node.js的异步实现 专栏的第五篇文章<Node.js的异步实现>.之前介绍了Node.js的事件机制,也许读者对此尚会觉得意犹未尽,因为仅仅只是简单的事件机制,并不能道尽No ...