HDU 4719 Oh My Holy FFF（DP+线段树）（2013 ACM/ICPC Asia Regional Online ―― Warmup2）

Description

N soldiers from the famous "*FFF* army" is standing in a line, from left to right.

 o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o   o /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \

You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:

 o   o   o  |  o   o   o   o  |  o   o   o   o   o   o  |  o   o   o   o   o /F\ /F\ /F\ | /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\ / \ / \ / \ | / \ / \ / \ / \ | / \ / \ / \ / \ / \ / \ | / \ / \ / \ / \ / \

In your opinion, the number of soldiers in each group should be no more than L.  Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be b _i > b _i-1.  You give your division a score, which is calculated as 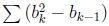, b ₀ = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.  Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.

 

Input

The first line has a number T (T <= 10) , indicating the number of test cases.  For each test case, first line has two numbers N and L (1 <= L <= N <= 10 ⁵), as described above.  Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= H _i <= 10 ⁵)

 

Output

For test case X, output "Case #X: " first, then output the best score.

题目大意：有n个数，划分为多个部分，假设M份，每份不能多于L个。每个数有一个h[i]，每份最右边的那个数要大于前一份最右边的那个数。设每份最右边的数为b[i]，求最大的sum{b[i]² - b[i - 1]}，1≤i≤M，其中b[0] = 0。

思路：朴素DP为，dp[i]表示以i为结尾的最大划分。那么dp[i] = max{dp[j] - h[j] + h[i]²}，1≤i-j≤L，h[j]＜h[i]。这种会超时，采取线段树优化。因为有两个限制，考虑到若h[j]≥h[i]，那么求i的时候一定不会用到j，那么先按h排序再DP（h相同的，i大的排前面）。

PS：又忘了把int改成long long >_<

代码（781MS）：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 typedef long long LL;
 
 const int MAXN = ;
 
 LL dp[MAXN];
 int n, L;
 LL tree[MAXN << ], maxt[MAXN << ];
 
 void pushdown(int x) {
     int ll = x << , rr = ll ^ ;
     if(tree[x] != -) {
         tree[ll] = max(tree[x], tree[ll]);
         tree[rr] = max(tree[x], tree[rr]);
         maxt[ll] = max(maxt[ll], tree[x]);
         maxt[rr] = max(maxt[rr], tree[x]);
         tree[x] = -;
     }
 }
 
 void update(int x, int left, int right, int a, int b, LL val) {
     if(a <= left && right <= b) {
         tree[x] = max(tree[x], val);
         maxt[x] = max(maxt[x], val);
     }
     else {
         pushdown(x);
         int ll = x << , rr = ll ^ ;
         int mid = (left + right) >> ;
         if(a <= mid) update(ll, left, mid, a, b, val);
         if(mid < b) update(rr, mid + , right, a, b, val);
         maxt[x] = max(maxt[x], max(maxt[ll], maxt[rr]));
     }
 }
 
 LL query(int x, int left, int right, int a, int b) {
     if(a <= left && right <= b) return maxt[x];
     else {
         pushdown(x);
         int ll = x << , rr = ll ^ ;
         int mid = (left + right) >> ;
         LL ret = -;
         if(a <= mid) ret = max(ret, query(ll, left, mid, a, b));
         if(mid < b) ret = max(ret, query(rr, mid + , right, a, b));
         return ret;
     }
 }
 
 struct Node {
     int h, pos;
     void read(int i) {
         pos = i;
         scanf("%d", &h);
     }
     bool operator < (const Node &rhs) const {
         if(h != rhs.h) return h < rhs.h;
         return pos > rhs.pos;
     }
 } a[MAXN];
 
 LL solve() {
     sort(a + , a + n + );
     dp[n] = -;
     memset(tree, , sizeof(tree));
     memset(maxt, , sizeof(maxt));
     update(, , n, , , );
     for(int i = ; i <= n; ++i) {
         LL tmp = query(, , n, max(, a[i].pos - L), a[i].pos - );
         if(tmp == -) {
             if(a[i].pos == n) break;
             else continue;
         }
         dp[a[i].pos] = tmp + LL(a[i].h) * a[i].h;
         if(a[i].pos == n) break;
         update(, , n, a[i].pos, a[i].pos, dp[a[i].pos] - a[i].h);
     }
     //for(int i = 1; i <= n; ++i) printf("%I64d\n", dp[i]);
     return dp[n];
 }
 
 int main() {
     int T; scanf("%d", &T);
     for(int t = ; t <= T; ++t) {
         scanf("%d%d", &n, &L);
         for(int i = ; i <= n; ++i) a[i].read(i);
         LL ans = solve();
         if(ans == -) printf("Case #%d: No solution\n", t);
         else printf("Case #%d: %I64d\n", t, ans);
     }
 }