CF 1091E New Year and the Factorisation Collaboration

昨晚Good Bye 2018D题没做出来，车翻大了……

官方题解      传送门

初赛知识：一个无向图所有顶点度数之和为偶数。然而这东西还有一个高端的名字：Handshaking lemma

但是这并不是本题的重点，另外一个看上去很高端的东西才是本题的重点：Erdős–Gallai theorem

对于一个无向图的度数序列$d$，先从大到小排序，即满足$d_1 \geq d_2 \geq d_3 \geq \dots \geq d_n$，

那么对于$\forall k \in [1, n]$，均满足

$$\sum_{i = 1}^{k}d_i \leq k(k - 1) + \sum_{i = k + 1}^{n}min(k, d_i)$$

意思就是先选出度数前$k$大的点然后让它们生成一张完全图，然后剩下的点无论怎么连一定是一张合法的无向图。

我们注意到在这题中，如果$x，y$是两个合法的答案（不妨设$x<y$），那么如果$z$满足$z \in (x, y)$并且$x \mod 2 == z \mod 2$，$z$也是一个合法的答案。也就是说，我们只要做出这个答案的区间$[L, R]$，然后检验每一个$i \in [L, R]$是否满足那个初赛知识就好了。

考虑如何找这个区间。

首先把度数序列从大到小排个序然后弄个前缀和，我们去扫描每一个位置，把当前扫到的位置$i$作为Erdős–Gallai theorem中的$k$，因为后面都是有序序列，所以那个$min$只要二分找到一个分界点$j$使左边都大于$i$，右边都小于等于$i$，结合前缀和就可以算出式子两边的值。

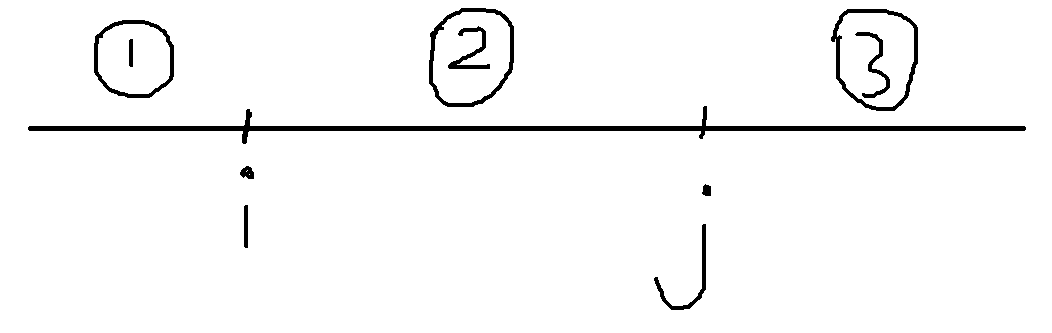
假设左边的和为$a$，右边的和为$b$，考虑$n + 1$个点可以放在哪个位置（假设第$n + 1$个点的度数为$x$），有以下几种情况：

1、$a > b$，如果$a > b + i$，那么直接无解。

2、观察到当$n + 1$个点放在$3$的时候，有$b + x \geq a$，那么$x \geq a - b$。

3、当$n + 1$个点放在$1$的时候，第$i$个位置实际上变成了第$i + 1$个位置，但是这并不影响前缀和的计算，这时候满足$a - d_i + x \leq b + i$，那么$x \leq b + i - a + d_i$。

时间复杂度$O(nlogn)$。

#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;

const int N = 5e5 + ;

int n;
ll a[N], sum[N];
vector <int> ans;

bool cmp(ll x, ll y) {
    return x > y;
}

template <typename T>
inline void read(T &X) {
    X = ; char ch = ; T op = ;
    for (; ch > ''|| ch < ''; ch = getchar())
        if (ch == '-') op = -;
    for (; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

template <typename T>
inline void chkMin(T &x, T y) {
    if (y < x) x = y;
}

template <typename T>
inline void chkMax(T &x, T y) {
    if (y > x) x = y;
}

int main() {
    read(n);
    for (int i = ; i <= n; i++) read(a[i]);
    sort(a + , a +  + n, cmp);
    for (int i = ; i <= n; i++) sum[i] = sum[i - ] + a[i];

    ll ln = , rn = n;
    for (int i = ; i <= n; i++) {
        int j = lower_bound(a +  + i, a +  + n, i, cmp) - a;
        ll lsum = sum[i], rsum = 1LL * (j - i - ) * i + sum[n] - sum[j - ] + 1LL * i * (i - );
        if (lsum > rsum) {
            if (lsum - rsum > i) return puts("-1"), ;
            chkMax(ln, lsum - rsum);
        }
        chkMin(rn, a[i] + rsum + i - lsum);
    }

    for (int i = ln; i <= rn; i++)
        if (!((i - sum[n]) & )) ans.push_back(i);

    if (ans.empty()) puts("-1");
    else {
        int siz = ans.size();
        for (int i = ; i < siz; i++)
            printf("%d%c", ans[i], i == siz -  ? '\n' : ' ');
    }

    return ;
}