HDU 5382 莫比乌斯反演

题目大意：

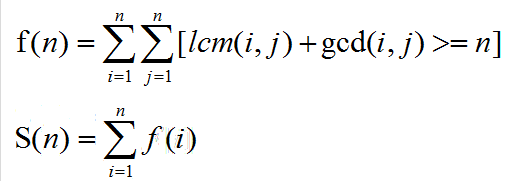
求S(n)的值 n<=1000000

这是官方题解给出的推导过程，orz，按这上面说的来写，就不难了

这里需要思考的就是G(n)这个如何利用积性函数的性质线性筛出来

作为一个质数，那么肯定G(i) = 2

1. 那么一个数 i 乘上了一个未出现的素数prime，那么就相当于，在当前符合的因子上面都乘了prime之后依旧符合，而原来 i 对应的数也符合，那么说明翻了两倍

也就是 g(i*prime) = 2*g(i) = g(prime) * g(i)

2. 如果这个乘上的素数prime已经存在于 i 中 ， 那么仔细想一下，只有 i 那些符合的因子中已经带prime的必须再乘上这个prime，不然这个prime跑到 i/d中，gcd = prime了，其他的都不变，说明其实 g(i*prime) = g(i) 的

 #include <bits/stdc++.h>

 using namespace std;
 #define N 1000000
 #define ll long long
 const int MOD=;

 ll g[N+] , t[N+] , f[N+];
 ll sum[N+];
 int prime[N/] , tot;
 bool check[N+];

 void get_g()
 {
     g[] = ;
     for(int i= ; i<=N ; i++){
         if(!check[i]) prime[tot++] = i , g[i] = ;
         for(int j= ; j<tot ; j++){
             if((ll)prime[j]*i>N) break;
             check[prime[j]*i] = true;
             if(i%prime[j]) g[prime[j]*i] = g[prime[j]]*g[i];
             else {g[prime[j]*i]=g[i]; break;}
         }
     }
 }

 void get_t()
 {
     for(int k= ; k<=N ; k++)
         for(int i=k ; i<=N ; i+=k)
             t[i] = (t[i]+g[k-])%MOD;
 }

 void get_f()
 {
     for(int i= ; i<=N ; i++)
         f[i] = (f[i-]+*i--t[i-])%MOD;
 }

 void init()
 {
     get_g();
     get_t();
     get_f();
     for(int i= ; i<=N ; i++) sum[i] = (sum[i-]+f[i])%MOD;
 }

 int main()
 {
     //freopen("a.in" , "r" , stdin);
     init();
     int T , n;
     scanf("%d" , &T);
     while(T--){
         scanf("%d" , &n);
         printf("%I64d\n" , sum[n]);
     }
     return ;
 }