(四)Logistic Regression

1 线性回归

回归就是对已知公式的未知参数进行估计。线性回归就是对于多维空间中的样本点，用特征的线性组合去拟合空间中点的分布和轨迹，比如已知公式是y=a∗x+b，未知参数是a和b，利用多真实的(x,y)训练数据对a和b的取值去自动估计。估计的方法是在给定训练样本点和已知的公式后，对于一个或多个未知参数，机器会自动枚举参数的所有可能取值，直到找到那个最符合样本点分布的参数（或参数组合）。也就是给定训练样本，拟合参数的过程，对y= a*x + b来说这就是有一个特征x两个参数a b，多个样本的话比如y=a*x1+b*x2+...，用向量表示就是y = 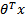，就是n个特征，n个参数的拟合问题（假设x0 与最后的偏置项写在一起）。

2 Logistic 回归

回归一般是针对输出Y为连续性变量的，当Y离散时，问题就变成了分类。

Logistic regression （逻辑回归）是当前业界常用于分类的机器学习方法，用于估计某种事物的可能性。可以简单把这个模型想象为一个服从参数为θ的概率分布，给定向量x，得到的y值就是分布函数值，最后根据分布函数值的大小来判断分类的类别。事实上这个分布也确实存在，就是Logistic 分布。

2.1 Logistic分布：

若随机变量X服从Logistic分布，则

对应的图形如下：

公式中u代表f(x)的中心位置，也是F(x)拐点的横坐标，r控制速率，r越小，F(x)的图形越陡，x的取值为实数域R，y取值为0-1，下面来看logistic模型

对输入向量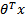，其取值也是整个x轴的，假设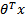服从Logistic(0,1),即u=0，r=1，带入到logistic分布中有

这便是标准的logistic函数，也可用如下公式表示：

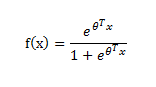
2.2二分类问题

用标签 0，1分别表示不同类别，对于训练样本x进行如下映射，便能得到一个介于0-1之间的值，对于2分类问题，该值>0.5，就分类为1，否则分类为0，该数值结余0-1之间，比如该数值是0.7，则说明了分类为1的概率是0.7，所以0.7分类为1；若为0.3，则说明分类为1的概率为0.3，也即分类为0的概率为0.7，所以最后0.3分类为0，用Y来表示类别，有：

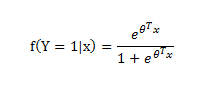
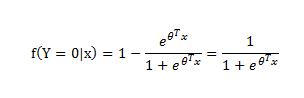
　　　　公式2.1

所以训练好的模型也就有了参数ϴ，直接对向量x进行映射即可得到分类结果。

Logistic模型的训练

根据公式2.1，有P(Y=1|x,ϴ) = f(x),P(Y=0|x,ϴ) = 1- f(x)

则P(y|x,ϴ) = f(x)^y(1-f(x))^1-y,y取0或者1即对应分类为0或者1的问题

Logistic的有一个特性，首先用p表示P（y=1|x,ϴ）,则1-p表示P（y=0|x,ϴ），一个事件发生的机率（odds）定义为事件发生的概率与不发生的概率的比值。设发生的概率为p，不发生的概率为1-p，那么事件的机率是

p1−p 代入公式有

可见事件发生的对数几率为x的线性函数。

2.3 Logistic的参数

1）极大似然估计法MLE

训练过程可以采用MLE算法，求解参数ϴ

取n个训练样本极对应标签，对每个样本p(y|x,ϴ),似然函数的形式如下：

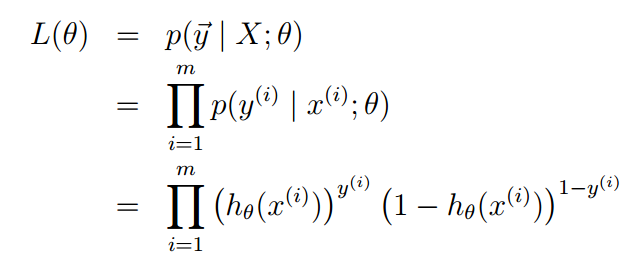
写成对数似然的形式

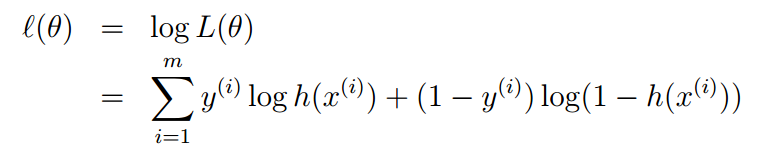
于是问题转变成了对l(ϴ)求极大值，另l(ϴ)最大的ϴ即为所求参数。怎么样求ϴ呢，这里可以采用梯度上升算法，因为要求得ϴ的最大值

注意g(ϴ^Tx)的到导数g'(ϴ^Tx)=g(ϴ^Tx)(1 - g'(ϴ^Tx))

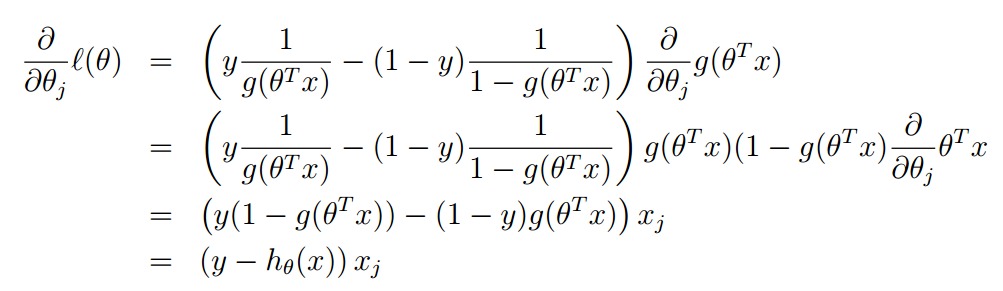
对每个ϴ_j均执行梯度上升即可求得最终结果ϴ，从而得到最终模型。

for each ϴ_jin ϴ：

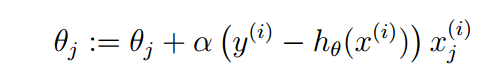
2）对数损失函数

　　对于logistic回归的参数估计除了最大似然外，还可以定义log损失函数

可见当实际标签为1时，h_ϴ(x)介于(0,1)之间，-log(h_ϴ(x))的图形如上所示，可见h_ϴ(x)越大，损失函数值(-log(h_ϴ(x))就越小，反之对于y=0

根据损失函数的定义，J(ϴ) = 1/m(Cost(_ϴ(x) , y))，并且把logistic的损失函数写到一起有：

当y=1与y=0时，分别对应了不同的损失函数，且y也只能取0或者1。

-log(1-z)的图形如右图所示，其损失函数的示意图如左图所示，这样一个数学公式，巧妙地解决了logistic的损失函数问题。

这便是是最终的损失函数，现在只要求出使得损失函数极小化的ϴ即可。因为log损失函数也为凹函数，所以可以选择梯度下降来求解，且其求解的公式类似于liner regression。

顺带提一下除了Graident Descent之外，还有其他的优化算法：

分别为共轭梯度下降法(CGD)，拟牛顿法(BFGS)与L-BFGS。求缺点如上所示。

2.4 决策边界：

下图为sigmod函数的图形，当ϴ^Tx>0时，有g（ϴ^Tx）>0.5,则可预测为类别1.

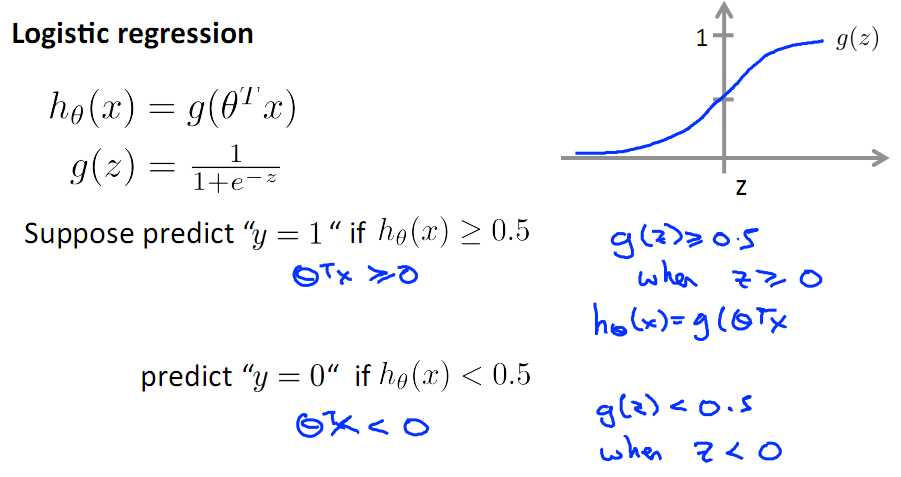
可见要把ϴ^Tx映射到sigmod函数里，它就对应了一个决策边界，因为sigmode函数为0.5对应了一个阈值，可以看下面线性决策边界示意图。

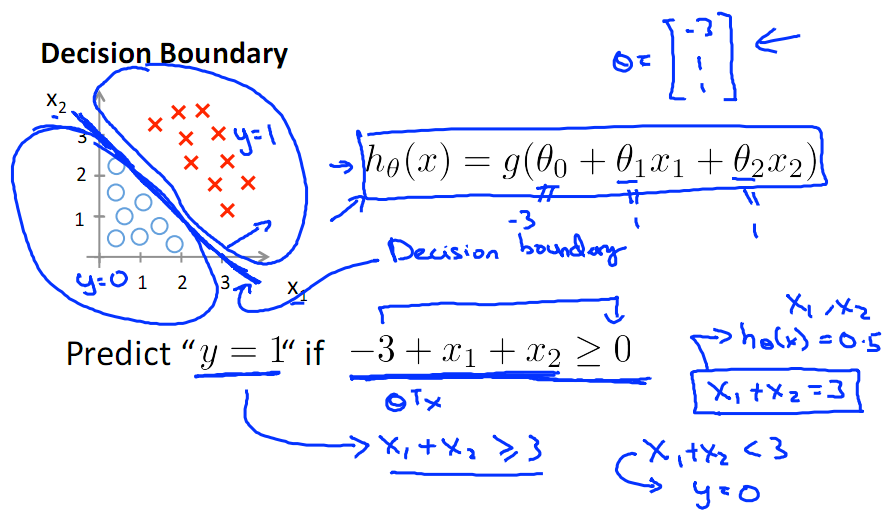
下面为非线性决策边界的示意图：

哎，这个线性不可分数据的参数是怎么来的呢？请听下回分解。

2.5 线性不可分时的处理

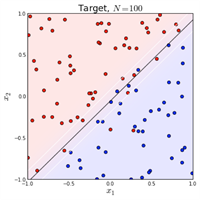
2.6多分类问题

如果y不是在[0,1]中取值，而是在K个类别中取值，这时问题就变为一个多分类问题。有两种方式可以出处理该类问题：一种是我们对每个类别训练一个二元分类器（One-vs-all），当K个类别不是互斥的时候，比如用户会购买哪种品类，这种方法是合适的。如果K个类别是互斥的，即 y=i 的时候意味着 y 不能取其他的值，比如用户的年龄段，这种情况下 Softmax 回归更合适一些。举个例子，判断一些动物的图片，并且将其归类为老鹰、鸟类，这种情况下，one -vs-all的分类方法是对老鹰和鸟类分别建立参数模型，从而老鹰也可以被分到鸟类，而softmax老鹰和鸟类根本不会分到一个类别，所以说softmax适用于对互斥类别的分类。Softmax 回归是直接对逻辑回归在多分类的推广，相应的模型也可以叫做多元逻辑回归（Multinomial Logistic Regression）。

one-vs-all 法

假设有n个类别，则为每个类别与其他类别的组合建立一个关于参数ϴ的模型，这样就会有n个参数向量ϴ_1...ϴ_N,分别套用每个参数向量方程，选取属于类别1-N中可能性最大的一个即可。如下所示：

Softmax Regression

在softmax回归中，首先给定训练样本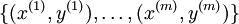，这时分类标签y不再只取0-1，而是有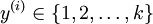，比如在MNIST手写识别数据库，有0-9 这10个数字，所以需要k=10

对输入x

3 总结

logistic在分类的同时，会给出其可能性，比如某用户买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。（注意这里是：“可能性”，而非数学上的“概率”，logisitc回归的结果并非数学定义中的概率值，不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和，而非直接相乘），logistic回归会给出一个分类的数值，此数值介于0-1之间，比如预测一个女生是否喜欢你，它不像SVM那样直接给出0或者1，而是给出0.4，0.6这样的数值，这样就会知道喜欢的程度，很多情况下我们需要回归产生一个类似概率值的0~1之间的数值（比如某一双鞋子今天能否卖出去？或者某一个广告能否被用户点击? 我们希望得到这个数值来帮助决策鞋子上不上架，以及广告展不展示）。这个数值必须是0~1之间，于是引入了Logistic方程，来做归一化。这里再次说明，该数值并不是数学中定义的概率值。

那么既然得到的并不是概率值，为什么我们还要费这个劲把数值归一化为0~1之间呢？归一化的好处在于数值具备可比性和收敛的边界，这样当你在其上继续运算时（比如你不仅仅是关心鞋子的销量，而是要对鞋子卖出的可能、当地治安情况、当地运输成本等多个要素之间加权求和，用综合的加和结果决策是否在此地开鞋店时），归一化能够保证此次得到的结果不会因为边界太大/太小导致覆盖其他feature 或被其他feature覆盖。（举个极端的例子，如果鞋子销量最低为100，但最好时能卖无限多个，而当地治安状况是用0~1之间的数值表述的，如果两者直接求和治安状况就完全被忽略了）这是用logistic回归而非直接线性回归的主要原因。到了这里，也许你已经开始意识到，没错，Logistic Regression 就是一个被logistic方程归一化后的线性回归，仅此而已。至于所以用logistic而不用其它，是因为这种归一化的方法往往比较合理（人家都说自己叫logistic了嘛呵呵），能够打压过大和过小的结果（往往是噪音），以保证主流的结果不至于被忽视。

3.1 Logistic Regression的适用性

1）可用于概率预测，也可用于分类。
并不是所有的机器学习方法都可以做可能性概率预测（比如SVM就不行，它只能得到1或者-1）。可能性预测的好处是结果又可比性：比如我们得到不同广告被点击的可能性后，就可以展现点击可能性最大的N个。这样以来，哪怕得到的可能性都很高，或者可能性都很低，我们都能取最优的topN。当用于分类问题时，仅需要设定一个阈值即可，可能性高于阈值是一类，低于阈值是另一类。
3）各feature之间不需要满足条件独立假设，但各个feature的贡献是独立计算的。
逻辑回归不像朴素贝叶斯一样需要满足条件独立假设（因为它没有求后验概率）。但每个feature的贡献是独立计算的，即LR是不会自动帮你combine 不同的features产生新feature的 (时刻不能抱有这种幻想，那是决策树,LSA, pLSA, LDA或者你自己要干的事情)。举个例子，如果你需要TF*IDF这样的feature，就必须明确的给出来，若仅仅分别给出两维 TF 和 IDF 是不够的，那样只会得到类似 a*TF + b*IDF 的结果，而不会有 c*TF*IDF 的效果。

参考文献：

http://blog.sina.com.cn/s/blog_890c6aa301015mya.html

http://www.cnblogs.com/guyj/p/3800519.html

http://blog.csdn.net/songrotek/article/details/41310861

http://dataunion.org/17006.html

http://blog.csdn.net/han_xiaoyang/article/details/49123419

Andrew Ng讲义

《统计学习方法》#Logistic一章