采样定理与SDM

1.信噪比=6.02N+1.76dB

对于这个经常引用的AD/DA转换器理论信噪比（SNR）公式，代表一个完美的N位ADC的理论性能。下面先计算N位模数转换器（ADC）的理论量化噪声。一旦通过计算均方根量化噪声电压，计算出理论信噪比（SNR）。分析了过采样对信噪比的影响。

2.量化噪声模型

理想转换器在对信号进行数字化时产生的最大误差为±$\frac12LSB$，如理想N位ADC的传输函数所示（图1）。跨过几个LSB以上的任何ac信号的量化误差可以通过具有峰值到峰值振幅q（LSB的权重）的不相关锯齿波来近似。另一种观察这种近似的方法是，实际量化误差同样可能发生在±$\frac12q$范围内的任何点上。尽管这种分析并不精确，但对于大多数应用来说，它也足够。

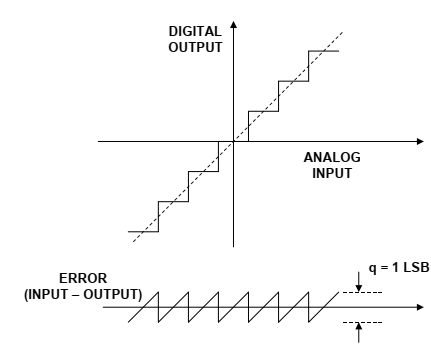
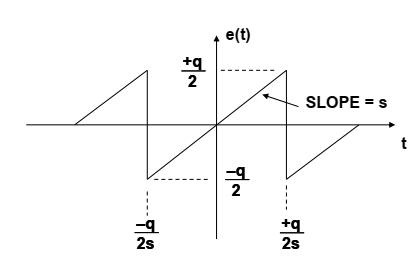
图1：理想N位ADC量化噪声 图2：量化噪声随时间的变化

图2中更详细地示出了量化噪声随时间的变化的函数。同样，简单的锯齿波为分析提供了足够精确的模型。锯齿形误差方程由下式给出：

$$e(t)=st，-\frac{q}{2s} < t {< + \frac{q}{2s}}   (1)$$

e(t)的均方值(平方和取平均), 量化噪声能量可以写成：

$$\bar{(e^2 (t) )}=\frac{s}q ∫_{-\frac{q}{2s}}^{\frac{q}{2s}}{(st)}^2 dt=q^2/12 （带内噪声值） (2)$$

因此,均方根(root mean square:rms)量化误差$=\sqrt[]{\bar{(e^2 (t) )}}=\frac{q}{\sqrt[]{12}} $ (3)

锯齿形误差波形产生的谐波远远超过奈奎斯特带宽dc至fs/2。然而，所有这些高次谐波必须折叠回到奈奎斯特带宽，并加在一起，以产生等于$\frac{q}{\sqrt[]{12}}$的均方根噪声。

由于量化误差为白噪声， 若采样频率为 fs，数据转换后的输出信号能量在在Nyquist带宽 0~fs/2 以内均匀地分布。则量化噪声的能量谱密度为:$e^2(f)=\frac{\frac{q^2}{12}}{fs/2} $（4）

理论信噪比现在可以在假设满标度输入正弦波的情况下计算：

满标度(FS)输入正弦波$v(t)=\frac{q∙2^N}{2} sin⁡(2πft) $(5)

满标度(FS)输入的rms值(功率开根号)=$\frac{q∙2^N}{2\sqrt[]{2}} $ (5-1)

因此一个理想N位转换器的RMS信噪比为:
$$SNR=20log_{10}⁡\frac{rms   value   of  FS  input}{rms value of quantization noise}=20log_{10}\frac{q∙2^N}{2\sqrt[]{2}}/\frac{q}{\sqrt[]{12}}=20log_{10}⁡2^N +20log_{10}⁡{\sqrt[]{\frac23}} $$

$SNR=6.02N+1.76dB$，dc到fs/2带宽之间 (8)

虽然量化噪声的实际频谱分析相当复杂，但简化分析得到的公式8对于大多数应用来说都足够精确。然而，必须再次强调的是，均方根量化噪声是在整个奈奎斯特带宽（dc到fs/2）上测量的。

3.量化噪声的频率特性

在许多应用中，实际感兴趣的信号占用较小的带宽BW，小于Nyquist带宽（见图3）。如果使用数字滤波来滤除带宽BW之外的噪声分量，则必须在等式中包括校正因子（称为处理增益），以解释等式9中产生的信噪比增加的部分。$SNR=6.02N+1.76dB+10log_{10}\frac{f_s}{2BW}$，实际信号带宽BW 内.

以大于其带宽两倍的速率fs对信号进行采样的过程称为过采样。过采样与量化噪声整形和数字滤波是sigma-delta转换器中的关键概念.

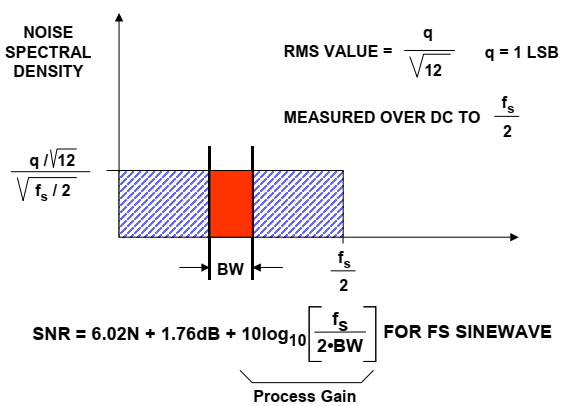
图3：显示处理增益的量化噪声谱

从下面的例子可以看出处理增益的重要性。在许多数字基站或其他宽带接收机中，信号带宽由多个单独的信道组成，单个ADC用于将整个带宽数字化。例如，假设信道带宽为30khz，占用大约12.5mhz的带宽。假设65-MSPS采样频率，并使用数字滤波分离各个30 kHz信道。在这些条件下，由于过采样而产生的过程增益由下式给出：

处理增益=$10log_{10}\frac{f_s}{2BW}=10log_{10}\frac{65\cdot10^6}{2\cdot30\cdot10^3}=30.3dB$(10)

如果ADC SNR规格是65dB（dc到fs/2），那么它在30khz信道带宽中增加到95.3dB（经过适当的数字滤波）。

图4显示了一个结合了过采样和欠采样的应用。感兴趣的信号具有带宽BW并且以载波频率fc为中心。采样频率可以远小于fc，并且选择的采样频率使得感兴趣的信号集中在其奈奎斯特区。模拟和数字滤波去除感兴趣的信号带宽之外的噪声。

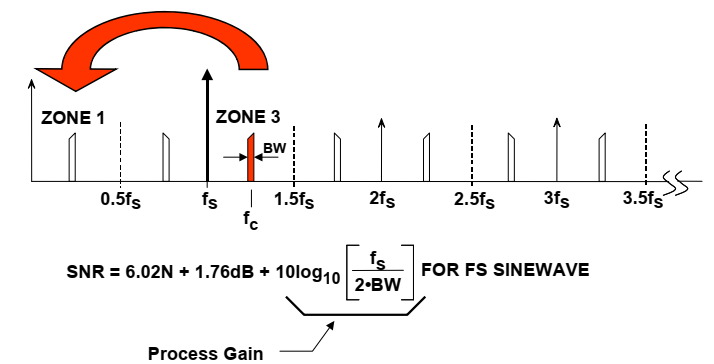
图4：欠采样和过采样组合导致过程增益

4.奈奎斯特准则

奈奎斯特准则要求采样频率至少是信号中包含的最高频率的两倍，否则有关信号的信息将丢失。如果采样频率小于最大模拟信号频率的两倍，则会出现称为混叠的现象。

为了理解混叠在时域和频域中的含义，首先考虑如图5所示采样的单音正弦波的时域表示的情况。在本例中，采样频率fs并没有满足至少是2fa，而是仅略高于模拟输入频率fa- Nyquist准则被违反。请注意，实际样本的模式会以较低一点的频率（fs–fa）产生锯齿正弦波。

 

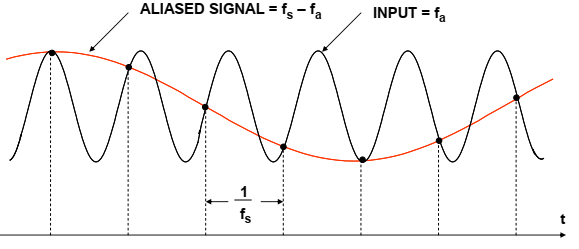
图5：时间域中的混叠 

图6B显示了这种情况下的相应频域表示。现在考虑由理想脉冲采样器在频率fs处采样的频率fa的单个频率正弦波的情况，假设fs>2fa，如图6A所示。采样器的频域输出在fs的每一个倍数周围显示原始信号的别名或图像，即在等于|±Kfs±fa |，K=1、2、3、4。

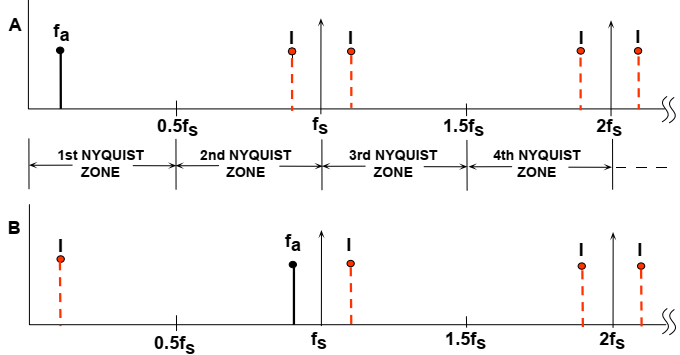
图6：使用理想采样器的模拟信号fa 采样率fs在|±Kfs±fa |，K=1,2...

奈奎斯特带宽定义为从dc到fs/2的频谱。频谱被分成无限个奈奎斯特区，每个区的宽度等于0.5fs，如图所示。在实际中，理想的采样器被ADC和FFT处理器所代替。FFT处理器仅提供从dc到fs/2的输出，即出现在第一Nyquist区域中的信号或混叠谱。

现在考虑第一奈奎斯特区以外的信号（图6B）。信号频率仅略小于采样频率，对应于图5中时域表示中所示的条件。注意，即使信号在第一个奈奎斯特区域之外，它的图像（或混叠谱）fs–fa也会落在第一Nyquist区域内部。回到图6A。

这与模拟混合过程类似，并且意味着需要在采样器（或ADC）之前进行一些滤波，以去除不在Nyquist带宽内、但其混叠分量落在Nyquist带宽内的频率分量。

5. 奈奎斯特准则应用

典型实时采样数据系统的框图如图7所示。在实际的模数转换之前，模拟信号通常经过某种信号调理电路，该电路具有放大、衰减和滤波等功能。需要低通/带通滤波器来去除感兴趣带宽之外的不需要的信号，并防止混叠。

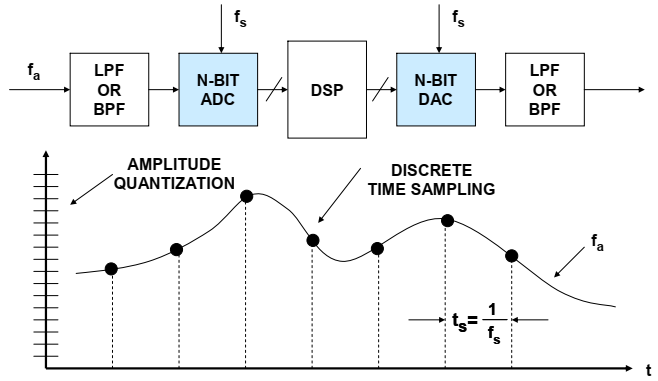
图7：典型采样数据系统

以fs的速率对输入ADC的信号进行连续采样，ADC以该速率向DSP呈现新的采样。为了保持实时操作，DSP必须在采样间隔1/fs内执行其所需的所有计算，并在ADC的下一个采样到达之前向DAC呈现一个输出采样。典型的DSP的例子就是数字滤波器。当必须将DSP数据转换回模拟信号时（例如，在声带或音频应用中），还需要DAC。

在实际的模数转换和数模转换过程中涉及到两个关键概念：离散时间采样和量化产生的有限振幅分辨率。本教程讨论离散时间采样。

6.采样保持放大器（SHA）

现在的大多数ADC都有一个内置的采样保持S/H(sample-and-hold)功能，从而允许它们处理交流信号。这种类型的ADC称为采样ADC。若不存在采样保持功能。如果输入到SAR ADC编码器的信号（假设没有SHA(采样保持)功能）在转换时间（示例中为8μs）期间变化超过1LSB，则输出数据可能具有较大的错误，这取决于编码的位置。大多数ADC架构都会受到这种类型的错误的影响。100kSPS=sample per second

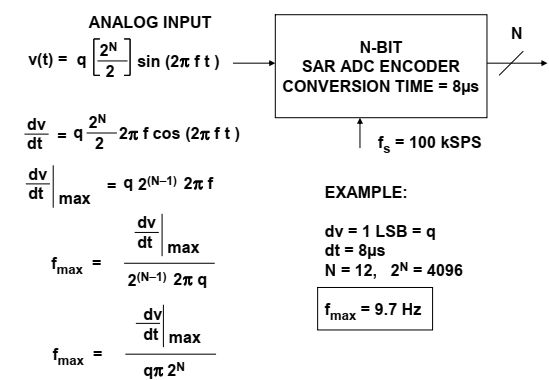
图8 非采样ADC（编码器）的输入频率限制

假设编码器的输入信号是具有满标度振幅（$\frac{q∙2^N}2$）的正弦波，其中q是1LSB的权重。 $v(t)= \frac{q∙2^N}{2}sin⁡(2πft) $

$$\frac{dv}{dt}=2πfq \frac{2^N}2 cos⁡(2πft) $$

因此，最大变化率为：$${\frac{dv}{dt}}_{max}=2πfq\frac{2^N}2$$

$$f=({{\frac{dv}{dt}}_{max}})/(πq2^N)$$

如果在转换时间$(dt=8μs)$内N=12，且允许1 LSB变化（dv=q），则可以解出fmax方程，即可以无误差地处理的最大满标度信号频率：fmax=9.7Hz。

这意味着，任何大于9.7Hz的输入频率都会受到转换误差的影响，即使8μs ADC的采样频率可能为fs=100ksps(T=10us)（这允许外部SHA在走出保持模式后重新获取信号有额外2μs间隔）。

为了处理交流信号，添加了一个sample and hold（SHA）函数，如图9所示。理想的SHA只是一个开关，驱动一个保持电容，然后是一个高输入阻抗缓冲器。缓冲器的输入阻抗必须足够高，以便电容器在保持时间内放电小于1LSB。SHA在采样模式下采样信号，并在保持模式期间保持信号恒定。调整定时以便编码器在保持时间期间执行转换。采样ADC因此可以处理快速信号。在所示示例中，采样和保持在2微秒内获取信号，编码器在8微秒内转换信号，产生10微秒的总采样周期。这产生100 kSPS的采样频率。以及处理高达50khz的输入频率的能力。

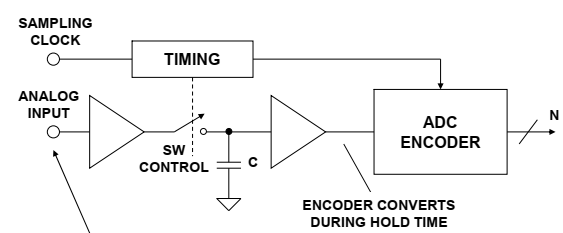
图9带采样保持的SAR ADC

7.基带抗混叠滤波器

基带采样意味着要采样的信号位于第一奈奎斯特区。需要注意的是，在理想采样器的输入端没有输入滤波的情况下，任何不在奈奎斯带宽内的但位于奈奎斯特区的频率分量（信号或噪声）将被混叠回第一奈奎斯特区。因此，几乎所有采样ADC应用中都使用抗混叠滤波器来消除这些不需要的信号。

假设感兴趣的信号最高频率是fa。抗混叠滤波器使dc到到fa的信号通过，同时衰减fa以上的信号。

假设滤波器的角频率被选择为等于fa。图10A说明了从最小衰减到最大衰减的有限过渡对系统动态范围的影响。

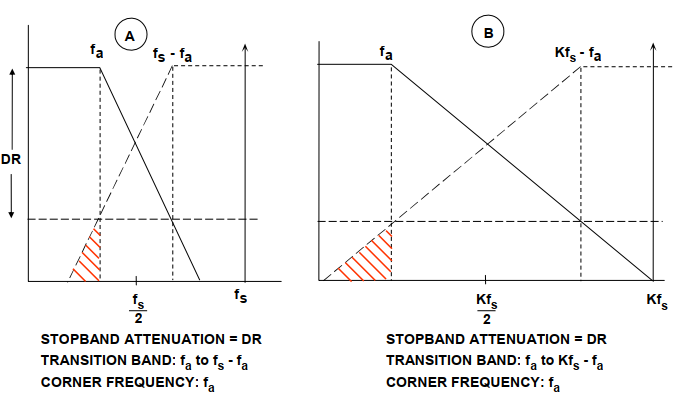
图10：过采样放宽了对基带抗混叠滤波器的要求

假设输入信号的满标度分量远高于感兴趣的最大频率fa。该图显示了高于fs–fa的满标度频率分量如何混叠回dc到fa之间的带宽内的。这些混叠分量与实际信号不可区分，因此将动态范围限制为图上的值，如DR。

一些文本建议针对奈奎斯特频率fs/2指定抗锯齿滤波器，但这假设感兴趣的信号带宽从dc扩展到fs/2，这是很少的情况。在图9A所示的示例中，fa和fs/2之间的混叠组件不受关注，也不限制动态范围。

因此，抗混叠滤波器过渡频带由拐角频率fa、阻带频率fs–fa（避免混叠的话，必须要求的阻带频率）和所需阻带衰减DR确定。根据信号保真度的要求选择所需的系统动态范围。

当过渡带变得更尖锐时，滤波器变得更复杂，我们可以看到抗混叠过渡带的锐度如何与ADC采样频率进行权衡。选择更高的采样率（过采样）可以降低对过渡带清晰度的要求（因此，滤波器的复杂性），但代价是使用更快的ADC并以更快的速率处理数据。如图10B所示，该图显示了在保持相同的模拟角频率fa和相同的动态范围DR要求的同时，将采样频率增加K倍的效果。较宽的过渡带（fa到Kfs–fa）使该滤波器比图10A的情况更易于设计。

8.delta调制

一位量化器的 sigma－delta 模拟示意图可以参考：

http://designtools.analog.com/dt/sdtutorial/sdtutorial.html

http://www.mathworks.com/matlabcentral/fileexchange

delta调制和差分PCM是通过在连续样本之间传输值的变化量（delta），而不是实际样本本身来实现更高的传输效率。

图11：delta调制和差分PCM

在增量调制中，模拟信号由图11A所示的一位ADC（比较器）量化。比较器输出用1位DAC转换回模拟信号，并在通过积分器后从输入中减去。模拟信号的形状如下发送：“1”表示自上一个样本以来已发生正偏移，“0”表示自上一个样本以来已发生负偏移。delta调制系统能够跟踪任何幅度的信号。理论上，没有削峰。然而，delta调制的理论限制是模拟信号不能变化太快。削坡问题如图12所示。在这里，尽管每个采样瞬间都指示正偏移，但模拟信号上升太快，并且量化器无法跟上。

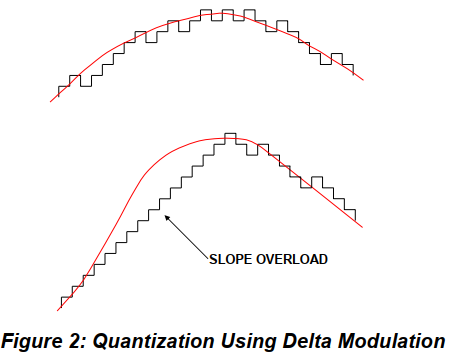
图12：使用delta调制的量化

增加量化步长或增加采样率可以减小斜率削波。

∑ΔADC包含非常简单的模拟电子器件（比较器、电压基准、开关、一个或多个积分器和模拟求和电路）和非常复杂的数字计算电路。该数字电路由数字信号处理器（DSP）组成，该数字信号处理器用作滤波器（通常但并非总是低通滤波器）。

下面在频域分析过采样技术，如果dc转换的量化误差高达1/2 LSB，则采样数据系统具有量化噪声。如图13A所示，一个完美的经典N位采样ADC在dc到fs/2的奈奎斯特频带内均匀分布有的均方根量化噪声（其中q是LSB的值，fs是采样率）。因此，其满标度正弦波输入的信噪比将为（6.02N+1.76）dB。如果ADC非理想值，且其噪声大于其理论最小量化噪声，则其有效分辨率将小于N位。它的实际分辨率（通常称为有效位数或ENOB）将由下式定义：$ENOB=\frac{(SNR-1.76dB)}{6.02dB}$ （17）

如果我们选择更高的采样率Kfs（见图13B），则rms量化噪声保持$\frac{q}{\sqrt[]{12}}$，但噪声现在分布在更宽的带宽dc到$Kf_s/2$。如果我们将数字低通滤波器（LPF）应用于输出，我们将去除大部分量化噪声，但不会影响所需信号，因此ENOB得到改进。用低分辨率ADC实现了高分辨率A/D转换。因子K通常被称为过采样率。同时过采样放宽了对模拟抗混叠滤波器的要求。特别是在消费类音频应用中，锐截止线性相位滤波器的成本非常高。

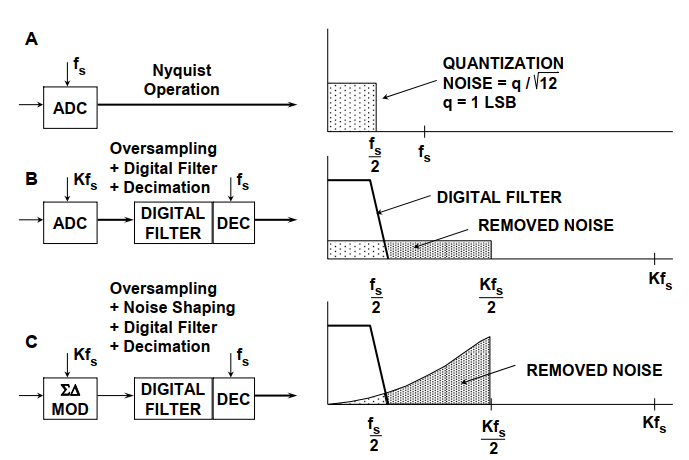
图13：过采样、数字滤波、噪声整形和抽取

当采样频率远大于 2倍的信号频率。由于量化噪声独立于采样频率, 所以采用过采样的量化噪声与采用奈奎斯特频率采样的量化噪声功率相同仍为, 但他却被分布到了一个更宽的带宽内。用于转换的输入信号通带为 0~fa，数据转换器的过采样率为$OSR=\frac{Kf_s}{2f_a}$，通带内的噪声能量$n^2$ 为：

$$n^2=\frac{e_{rms}^2}{Kfs/2}∙f_a=\frac{e_{rms}^2}{OSR}=\frac{q^2}{12OSR}=\frac{e_{rms}^2}{OSR}$$
$$SNR=10 log_{10}{⁡\frac{FS^2/2}{n^2}} =10 log_{10}{⁡\frac{FS^2/2}{\frac{e_{rms}^2}{OSR}}}=10 log_{10}{⁡\frac{FS^2/2}{\frac{q^2}{12OSR}}}$$

所以对于动态精度要求为 N 位的转换器，即满幅输入为$FS= q\cdot(2^{N-1})$,其理论上所能实现的信噪比为:

$$SNR=10 log_{10}{⁡\frac{FS^2/2}{\frac{q^2}{12OSR}}}=10 log_{10}{⁡\frac{{(q\cdot(2^{N-1})})^2/2}{\frac{q^2}{12OSR}}}==10 log_{10}{⁡(6∙(2^{N-1} )^2 ∙OSR)}$$
$$=10 log_{10⁡}2^{2N}+10 log_{10⁡}\frac{3}2+10 log_{10⁡}OSR≈6.02N+1.76+10 log_{10}⁡OSR$$

由于数字输出滤波器降低了带宽，输出数据速率可能低于原始采样速率（Kfs），并且仍然满足Nyquist准则。这可以通过将每kM结果传递给输出并丢弃剩余结果来实现。该过程被称为M的因子的“抽取”。 M可以有任何整数值，前提是输出数据速率大于信号带宽的两倍。抽取不会造成任何信息丢失（见图13B）。

如果我们简单地使用过采样来提高分辨率，由式（20）知我们必须过采样$2^{2N}$倍才能获得N位的分辨率提高。由于sigma-delta转换器不仅限制了信号的通带，而且还形成了量化噪声整形，因此不需要如此高的过采样率，如图13C所示，它的大部分噪声都落在通带之外。

如果我们取一个1位ADC（比较器），用积分器的输出驱动它，给积分器一个输入信号和一个1位DAC的输出相加，我们就得到一个一阶sigma-delta调制器，如图14所示。在数字输出端增加一个数字低通滤波器（LPF）和抽取器，我们就有一个sigma-deltaADC，sigma-delta调制器将量化噪声整形，使其位于数字输出滤波器的通带之上，因此ENOB比过采样率预期的要大得多。

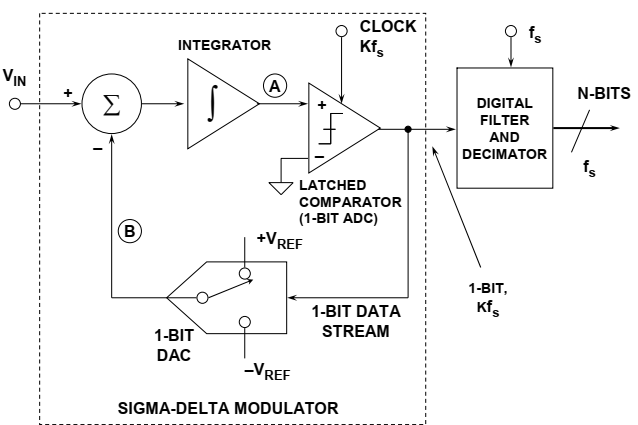
图14 1阶sigma-delta ADC

直观地说，∑-ΔADC的工作原理如下。假设在处有一个直流输入。积分器在节点A不断地上升下降。比较器的输出通过1bit DAC反馈到节点B的求和输入。从比较器通过1位DAC输出到求和点的负反馈回路将强制节点B处的平均直流电压等于$V_{in}$。这意味着平均DAC输出电压必须等于输入电压$V_{in}$。平均DAC输出电压由比较器输出的1位数据流中1的密度控制。当输入信号向$+V_{REF}$方向增加时，串行比特流中的“1”个数增加，“0”个数减少。类似地，当信号朝 –$V_{REF}$方向变为负时，串行比特流中的“1”个数减少，“0”个数增加。从一个非常简单的观点来看，这种分析表明，输入电压的平均值包含在比较器输出的串行比特流中。数字滤波器和抽取器处理串行比特流并产生最终输出数据。

对于在单个采样间隔内的任何给定输入值，来自1位ADC的数据实际上毫无意义。只有当对大量样本进行平均时，才会产生有意义的值。由于单比特数据输出具有明显的随机性，所以∑-Δ调制器很难在时域内进行分析。如果输入信号接近正满标度，很明显比特流中的“1”将多于“0”。同样地，对于接近负满标度的信号，比特流中的“0”将多于“1”。对于接近中刻度的信号，“1”s和“0”s的数量大致相等。图15显示了两种输入条件下积分器的输出。第一种是输入为零（中刻度）。要解码输出，请将输出样本通过一个简单的数字低通滤波器，该滤波器平均每四个样本。滤波器的输出为2/4。该值表示双极零点。如果平均更多的样本，则获得更多的动态范围。例如，平均4个样本可获得2位分辨率，而平均8个样本可获得4/8或3位分辨率。在图5的底部波形中，4个样本的平均值为3/4，8个样本的平均值为6/8。

$$V_in=(N_1-N_0)×V_{REF}/N $$

N表示比较次数（样本数），$N_1$表示N次比较中1的个数，$N_0$表示N次比较中0的个数。

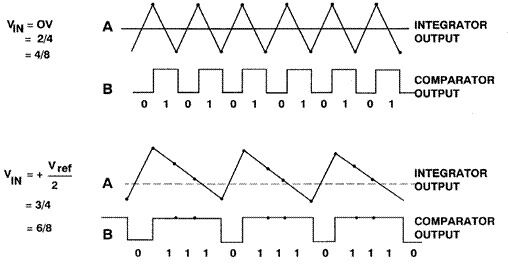
图15:Sigma-Delta调制器波形

由于数字滤波器是∑-ΔADC的一个组成部分，因此存在一个内置的“流水线”延迟（有时称为“延迟”），主要由数字滤波器中的抽头数决定。在sigma-deltaADC中的数字滤波器可以相当大（几百个抽头），因此在多路复用应用中，延迟可能成为一个问题，在切换信道后必须允许适当的稳定时间。

9.sigma-deltaADC的频域分析与噪声整形

噪声整形的概念最好在频域中通过考虑图16中的简单sigmadelta调制器模型来解释。

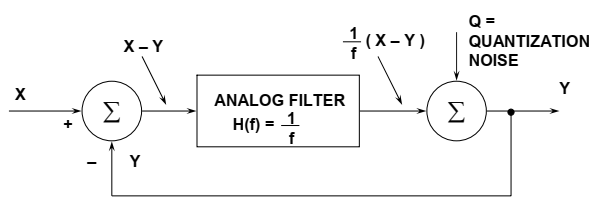
图16:Sigma-Delta调制器的简化频域线性化模型

$$Y=\frac{1}f (X-Y)+Q→(f+1)Y=X+fQ (22)$$

$$Y=\frac{X}{f+1}+\frac{fQ}{f+1} (23)$$

信号项 ：噪声项

调制器中的积分器表示为具有等于H(f)=1/f的传递函数的模拟低通滤波器。该传递函数具有与输入频率成反比的振幅响应。1位量化器产生量化噪声Q，该量化噪声Q被注入到输出求和块中。如果我们让输入信号为X，输出信号为Y，则从输入求和出来的信号必须为X–Y。这将乘以滤波器传递函数1/f，结果将转到输出求和的一个输入。通过检查，我们可以将输出电压Y的表达式写成：

\(Y=\frac{1}f (X-Y)+Q\)，$Y=\frac{X}{f+1}+\frac{fQ}{f+1} $

注意，当频率f接近零时，输出电压Y接近X，而无噪声分量。在较高的频率下，信号分量的幅度接近于零，噪声分量接近于Q。在较高的频率下，输出主要由量化噪声组成。实质上，模拟滤波器对信号具有低通效应，而对量化噪声具有高通效应。因此，模拟滤波器在∑-Δ调制器模型中执行噪声整形功能。

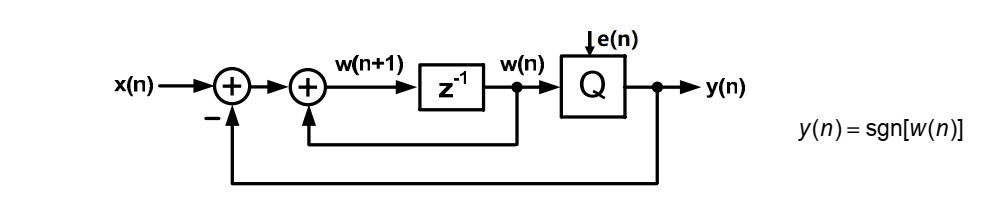
1bit sigma-delta 量化器时域模型

$w(n+1)=w(n)+x(n)-y(n) n=1,2,....N$

$w(N+1)-w(1)=∑_{n=1}^N[x(n)-y(n)]$

$$
\begin{aligned}
\lim_{N\to \infty} \tfrac{w(N+1)-w(1)}{n}=\lim_{N\to \infty} \frac{1}{N}∑_{n=1}^Nx(n)-\lim_{N\to \infty} \frac{1}{N}∑_{n=1}^NY(n)
\end{aligned}
$$

假设环路稳定，则w(n)有界，所以$0=\bar{x} -\bar{y}$，数字输出的平均值y与输入近似相等，离散时间积分器输入的平均值等于零。

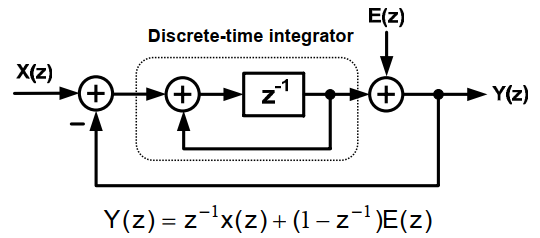
1bit 1阶 sigma –delta量化器的z域模型

$$Y(z)= z^{-1}X(z)+(1-z^{-1})E(z)$$
$STF(z)为z^{-1}，NTF(z)为(1-z^{-1})$，

\[|NTF(z)|=| 1-z^{-1}|=|1-e^{-jwT}|=|1-e^{-j2πf/f_s}|=|2sin(πf/f_s )|,
\]

已知，在(0,fs/2)之间均匀分布的白噪声功率为$q^2/12$，噪声的功率谱密度为 $\frac{q^2/12}{fs/2}$，整形后信号带宽内的噪声功率为:
$$P_n=∫_{-f_B}^{f_B}\frac{q^2/12}{fs/2} |NTF(z)|^2df=∫_{-f_B}^{f_B}\frac{q^2/12}{fs/2}|2sin(πf/f_s )|^2≈\frac{q^2}{12}\frac{π^2}{3} \frac{1}{OSR^3} $$
此时根据式（20）得到：

$$SNR=10 log_{10}{⁡\frac{FS^2/2}{\frac{π^2}{3} \frac{1}{OSR^3}{\frac{q^2}{12}}}}=10 log_{10}{⁡\frac{{(q\cdot(2^{N-1})})^2/2}{\frac{π^2}{3} \frac{1}{OSR^3}{\frac{q^2}{12}}}}$$
$$=10 log_{10⁡}\frac9{2π^2 }+10 log_{10}⁡2^{2N} +30 log_{10}{⁡OSR}=-3.41+6.02N+10 log_{10}⁡OSR^3 $$

可知当 OSR 提高一倍，信噪比提高 9dB，即增加 1.5bit 的 ADC有效分辨率。

1bit 2阶 sigma –delta量化器的z域模型

$$P_n=∫_{-f_B}^{f_B}\frac{q^2/12}{fs/2} |NTF(z)|^2|NTF(z)|^2df=∫_{-f_B}^{f_B}\frac{q^2/12}{fs/2}|2sin(πf/f_s )|^4≈\frac{q^2}{12}\frac{π^4}{5} \frac{1}{OSR^5} $$
$$SNR=-11.14+6.02N+10 log_{10⁡}OSR^5=-11.14+6.02N+50 log_{10⁡}OSR $$

可以看出，在二阶调制器中， OSR 每增加一倍，信噪比提高 15dB。在同样的过采样率时，可以获得比一阶调制器更高的信噪比和信号精度。

对于给定的输入频率，高阶模拟滤波器提供更多的衰减。通过在∑-Δ调制器中使用一个以上的积分和求和级，我们可以实现更高阶的量化噪声整形，对于给定的过采样率，甚至可以获得更好的ENOB，如图17所示，对于一阶和二阶∑-Δ调制器。

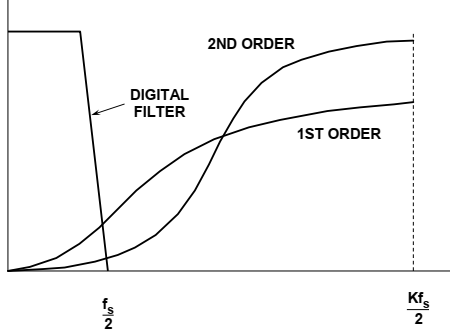
图17:Sigma-Delta调制器整形量化噪声

二阶∑-Δ调制器的框图如图18所示。

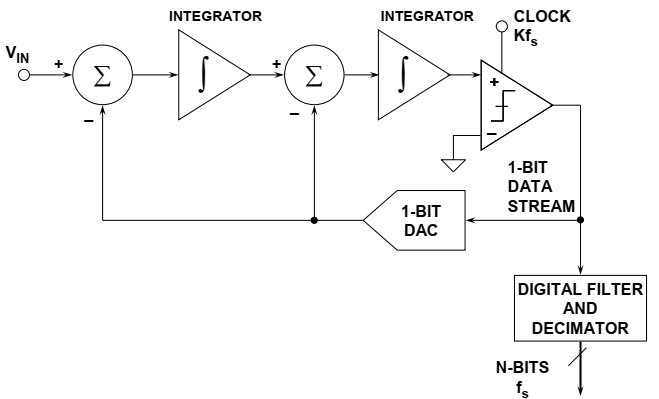
图18：二阶Sigma-Delta ADC

11.多级噪声整形（MASH）sigma-delta变换器

图21显示了三阶MASH ADC的框图。从第一DAC输出中减去第一积分器的输出以产生第一级量化噪声Q1。然后，Q1被第二阶段量化。从第二DAC输出中减去第二积分器的输出以产生第二级量化噪声，该第二级量化噪声依次被第三级量化。

第一阶段的输出加上第二阶段输出的单数字微分和第三阶段输出的双微分，以产生最终输出。结果是，量化噪声Q1被第二级抑制，量化噪声Q2被第三级抑制，产生与三阶环路相同的抑制。由于这一结果是由三个一阶回路得到的，因此保证了系统的稳定运行。

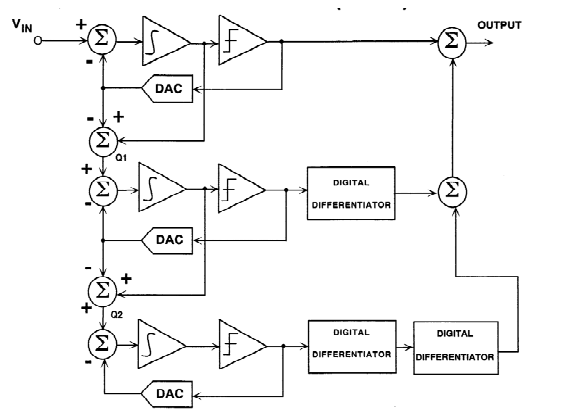
图21：多级噪声整形Sigma-Delta ADC（MASH）

对于K阶噪声整形：

$$NTF(z)={(1-z^{-1})}^K, | NTF(z)|_{z=e^{jw} }=[2sin(πf/f_s )]^K≈(2πf/f_s )^K,当f≪f_s时$$
$$P_n≅\frac{q^2}{12} \frac{π^{2K}}{2K+1} (OSR)^{2K+1}$$
$$SNR=6.02n+1.76+10log_{10⁡}\frac{2K+1}{π^{2K}} +(20K+10)log_{10}⁡OSR$$

过采样率OSR加倍,信噪比改善3(2K+1)dB或者(K+1/2)bit/octave。

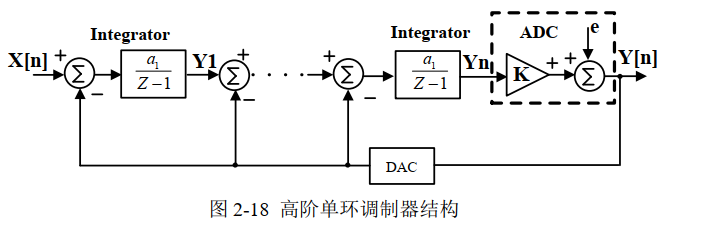
a_j为积分器的增益系数， k 为量化器增益。在低频段时，积分器增益较大，

图19显示了sigma-delta调制器的阶数与达到特定信噪比所需的过采样量之间的关系。例如，如果过采样率为64，则理想的二阶系统能够提供约80分贝的信噪比。这意味着大约有13个有效位（ENOB）。通过增加过采样率和/或使用高阶调制器，可以从1位系统获得附加分辨率。

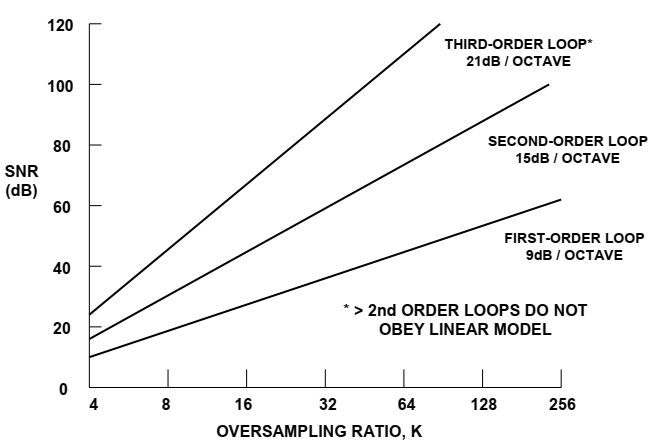
图19：一阶、二阶和三阶环路的信噪比与过采样比

所以对于1位A/D转换器的信噪比为6-dB，如果f_B=25kHz，对于直接过采样以及一阶噪声整形需要73Mhz和二阶需要5.7Mhz的采样率才能获得96-dB的信噪比（或16位）。

10.多位sigma-delta转换器

到目前为止，我们只考虑了包含一个单位ADC（比较器）和一个单位DAC（开关）的sigma-delta转换器。图20的框图显示了一个多位sigma-delta ADC，它使用一个n位flash ADC和一个n位DAC。显然，这种结构将为给定的过采样率和环路滤波器阶数提供更高的动态范围。动态范围(DR)：是指转换器最大输入信号和能检测到的最小输入信号能量的比值）

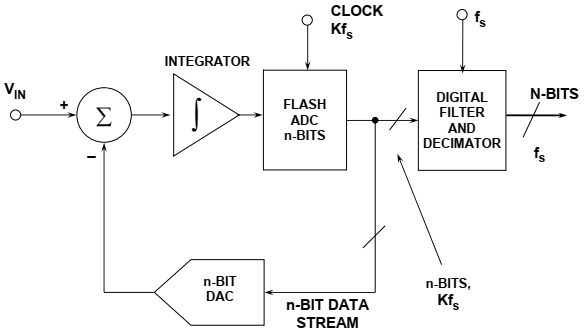
图20多位sigma-delta ADC

这种技术的真正缺点是线性度取决于DAC线性度，需要薄膜激光微调以接近16位的性能水平。这使得采用传统二进制数模转换器技术在混合信号集成电路上实现多位结构变得非常不切实际。