点&边双连通分量

双连通分量

参考博客：https://www.cnblogs.com/jiamian/p/11202189.html#_2

概念

双连通分量有点双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。

点双连通和边双连通

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 边双连通。

在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点（只能删去一个，且不能删 \(u\) 和 \(v\) 自己）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 点双连通。

边双连通具有传递性，即，若 \(x\),\(y\) 边双连通，\(y\),\(z\) 边双连通，则 \(x\),\(z\) 边双连通。

点双连通：删掉一个点之后，图仍联通

边双连通：删掉一条边之后，图仍联通

概述

在一个无向图中，若任意两点间至少存在两条“点不重复”的路径，则说这个图是点双连通的（简称双连通, biconnected）

在一个无向图中，点双连通的极大子图称为点双连通分量（简称双连通分量, Biconnected Component,BCC）

性质

1. 任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性，即 BCC 中无割点。

2. 若 BCC 间有公共点，则公共点为原图的割点。

3. 无向连通图中割点一定属于至少两个 BCC，非割点只属于一个 BCC。

算法

在 Tarjan 过程中维护一个栈，每次 Tarjan 到一个结点就将该结点入栈，回溯时若目标结点 \(low\) 值不小于当前结点 \(dfn\) 值就出栈直到目标结点（目标结点也出栈），将出栈结点和当前结点存入 BCC。

点双连通分量

我们从割点的定义可以得知，当你把割点去掉的时候原来的一个强连通分量会变成两个或以上的强连通分量，但是我们可以知道，去掉割点以外的点对于连通块的数量是没有影响的，所以我们可以知道，割点加上他能分成的连通块的各个点可以组成一个点双连通分量，就像下面这个图：

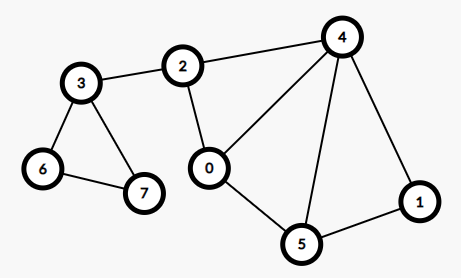
一眼能看出来的就是 \(2\)，\(3\) 都是割点，我们可以发现 \(3,6,7\) 和 \(0,1,2,3,4,5\) 都是点双连通分量。

我们根据上面提到的性质可以得知，割点至少在两个点双连通分量里，所以我们在弹栈存答案的时候不要把割点一起弹出，直到这个割点分出的连通块的点双连通分量都找完的时候再进行弹栈。

P8435 【模板】点双连通分量

code:

#include<bits/stdc++.h>
#define N 10001000
using namespace std;
struct sb{int u,v,next;}e[N];
int n,m,cnt,head[N],dfn[N],low[N],tot,stk[N],top,bcc;//bcc存放当前的点双连通分量的数量
vector<int>ans[N];//存放答案
inline void add(int u,int v)
{
	e[++cnt].u=u;
	e[cnt].v=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
inline void tarjan(int x,int fa)//fa是x的父节点
{
	dfn[x]=low[x]=++tot;
	stk[++top]=x;
	int ch=0;//ch存放子节点的数量
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(!dfn[v])//如果当前点还没有搜索过
		{
			ch++;//子节点加一
			tarjan(v,x);//继续往下搜
			low[x]=min(low[x],low[v]);//正常更新low[x]的值
			if(low[v]>=dfn[x])//割点的判定条件
			{
				bcc++;//点双连通分量的数量加1
				while(stk[top+1]!=v)//如果上一个弹出的栈顶元素不是v的话就一直弹
					ans[bcc].push_back(stk[top--]);//将当前点放入栈中
				ans[bcc].push_back(x);//最后把割点给加进去
			}
		}
		else if(v!=fa)//不能用父节点来更新当前点的low值
		  low[x]=min(low[x],dfn[v]);
	}
	if(fa==0&&ch==0)//特判只有一个点的情况
	  ans[++bcc].push_back(x);
}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])
		{
			top=0;
			tarjan(i,0);
		}
	}
	cout<<bcc<<endl;
	for(int i=1;i<=bcc;i++)
	{
		int siz=ans[i].size();
		cout<<siz<<" ";
		for(int j=0;j<siz;j++)
		  cout<<ans[i][j]<<" ";
		cout<<endl;
	}
	return 0;
}

另一种写法？

code：

void tarjan(int x,int fa)
{
	dfn[x]=low[x]=++tot;
	stk[++top]=x;
	if(x==fa&&head[x]==0)
	{
		ans[++bcc].push_back(x);
		return;
	}
	int ch=0;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v,fa);
			low[x]=min(low[x],low[v]);
			if(low[v]>=dfn[x])
			{
				ch++;
				if(x!=fa||ch>1)
					vis[x]=1;
				bcc++;
				int y;
				while(y!=v)
				{
					y=stk[top--];
					ans[bcc].push_back(y);
				}
				ans[bcc].push_back(x);
			}
		}
		else if(x!=fa)
		  low[x]=min(low[x],dfn[v]);
	}
}

边双连通分量

割边，也就是桥，会找吧，代码就和缩点有一点不同，就是把 if(low[v]>=dfn[x]) 改成 if(low[v]>dfn[x])。

我们都知道把割边去掉之后就会多出一些强连通分量，如果要是不是割边的话，那就对连通块的数量没有影响，所以我们可以找出所有的割边，然后 dfs 一遍找出连通块。

来看下面这张图

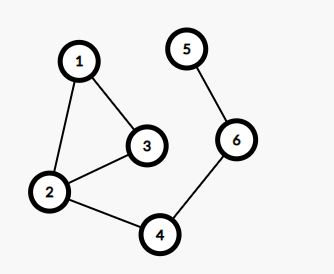
可以看出里面不是割边的边只有 {1，3}，{1，2}，{2，3}；我们可以发现一个 DCC 里面的边是没有割边的，所以我们把割边标记后 dfs 是正确的。

P8436 【模板】边双连通分量

code:

#include<bits/stdc++.h>
#define N 2000005
using namespace std;
int n,m,head[N],dfn[N],low[N],dcc,vis[N],tot,cnt=1;
struct sb{int u,v,next,flag;}e[N<<1];
vector<int>ans[N];
inline void add(int u,int v)
{
	e[++cnt].u=u;
	e[cnt].v=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
void tarjan(int x,int fa)
{
	dfn[x]=low[x]=++tot;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v,x);
			low[x]=min(low[x],low[v]);
			if(low[v]>dfn[x])
			  e[i].flag=e[i^1].flag=1;
		}
		else if(v!=fa)low[x]=min(low[x],dfn[v]);
	}
}
void dfs(int x)
{
	ans[dcc].push_back(x);
	vis[x]=1;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(vis[v]||e[i].flag)continue;
		dfs(v);
	}
}
signed main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;i++)
	  if(!dfn[i])
	    tarjan(i,0);
	for(int i=1;i<=n;i++)
	{
		if(!vis[i])
		{
			dcc++;
			dfs(i);
		}
	}
	cout<<dcc<<endl;
	for(int i=1;i<=dcc;i++)
	{
		int siz=ans[i].size();
		cout<<siz<<" ";
		for(int j=0;j<siz;j++)
		  cout<<ans[i][j]<<" ";
		cout<<endl;
	}
	return 0;
}