CF527D 题解

题意：数轴上有 \(n\) 个点，第 \(i\) 个点的坐标为 \(x_i\)，权值为 \(w_i\)。两个点 \(i,j\) 之间存在一条边当且仅当 \(abs(x_i-x_j)\geq w_i+w_j\)​ 。 你需要求出这张图的最大团的点数。

团的定义：两两之间有边的顶点集合。

solution:

可以先从式子入手。\(i,j\) 两点之间有边的条件是 \(\left|x_i-x_j\right|\ge w_i+w_j\)，然后考虑怎么把绝对值去掉，不妨设 \(x_i \ge x_j\)，然后式子就化简为了 \(x_i-x_j \ge w_i+w_j\)，遇到这种式子可以套路地把带有 \(i\) 的项移到一边，带有 \(j\) 的项移到另一边，所以式子就变成了:

\(x_i-w_i \ge x_j+w_j\) 在数轴上表示如图：

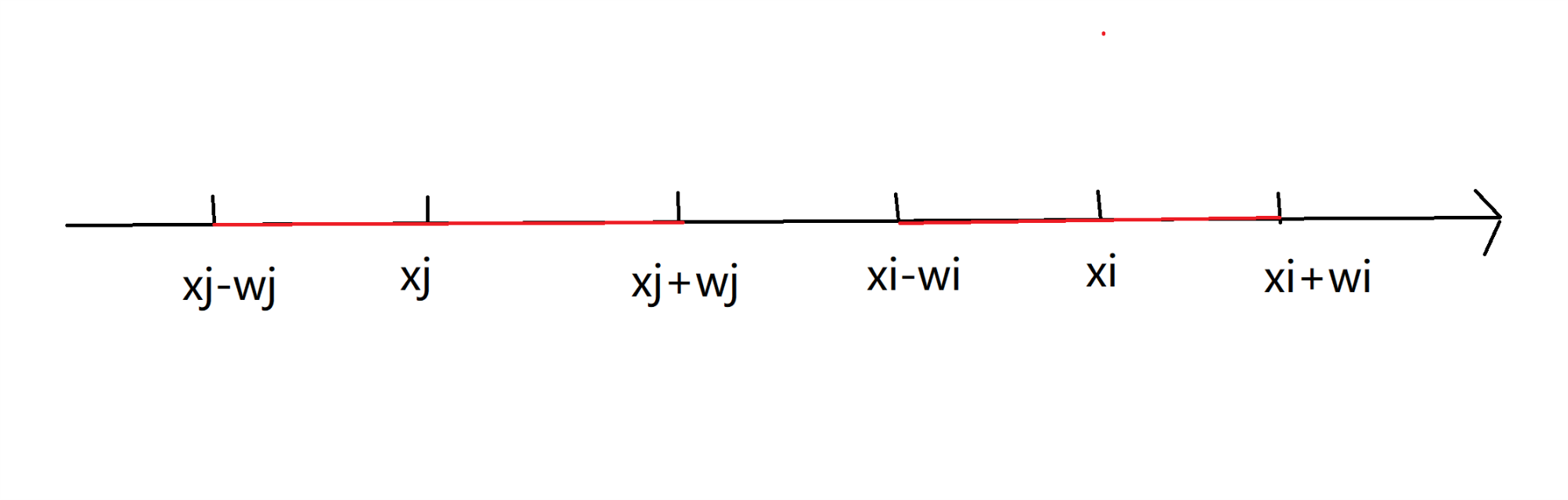
容易发现如果把一个点看成一条左端点为 \(x_k-w_k\)，右端点为 \(x_k+w_k\) 的线段，那么两个点之间有边当且仅当两条线段不重合，再根据团的定义：每两个点之间都有边。就转化为了任意两条线段都不重合，所以问题就变成了从 \(n\) 条线段里选择尽可能多的线段，使得任意两条线段都不重合，也就是线段覆盖问题。这里有一道线段覆盖的模板题，可以先完成。

代码（可读性应该还可以吧）：

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
int n,ans;
struct node{
	int l,r;
	bool operator < (const node &w) const{return r < w.r;}
}a[maxn];
int main(){
	scanf("%d",&n);
	int x,y;
	for(int i = 1;i <= n;i++){
		scanf("%d%d",&x,&y);
		a[i] = node{x - y,x + y};
	}
	sort(a + 1,a + n + 1);
	int nr = -2e9;
	for(int i = 1;i <= n;i++)
	if(a[i].l >= nr) nr = a[i].r,ans++;
	printf("%d",ans);
	return 0;
}