焦虑，不是IT公司贩卖给传统企业的！这个论断本身就不成立！数字化的动因是企业内部，生产中的七大浪费还不够么？数据不畅导致的决策失败还少吗？去问下企业业主，诸如此类的问题多了去了，数字化服务商只是来帮着他们解决这些问题而已，没理由背这个锅。

当然也不排除个别IT公司基于某些原因做了些不合时宜的宣传，但真正要起作用还是得有企业数字化内因的存在。

再说企业要想发展，必须数字化转型！数字化是企业在未来竞争中的立足之本！在数字化转型大潮中，企业如逆水行舟，不进则退。如果不进行数字化转型，那么企业将会被用户抛弃、被竞争对手超越、被市场边缘化，以致最终出局。另外数字化转型还可以捕获新的市场机会，尝试新的商业模式，在未来商业市场中提前占位。

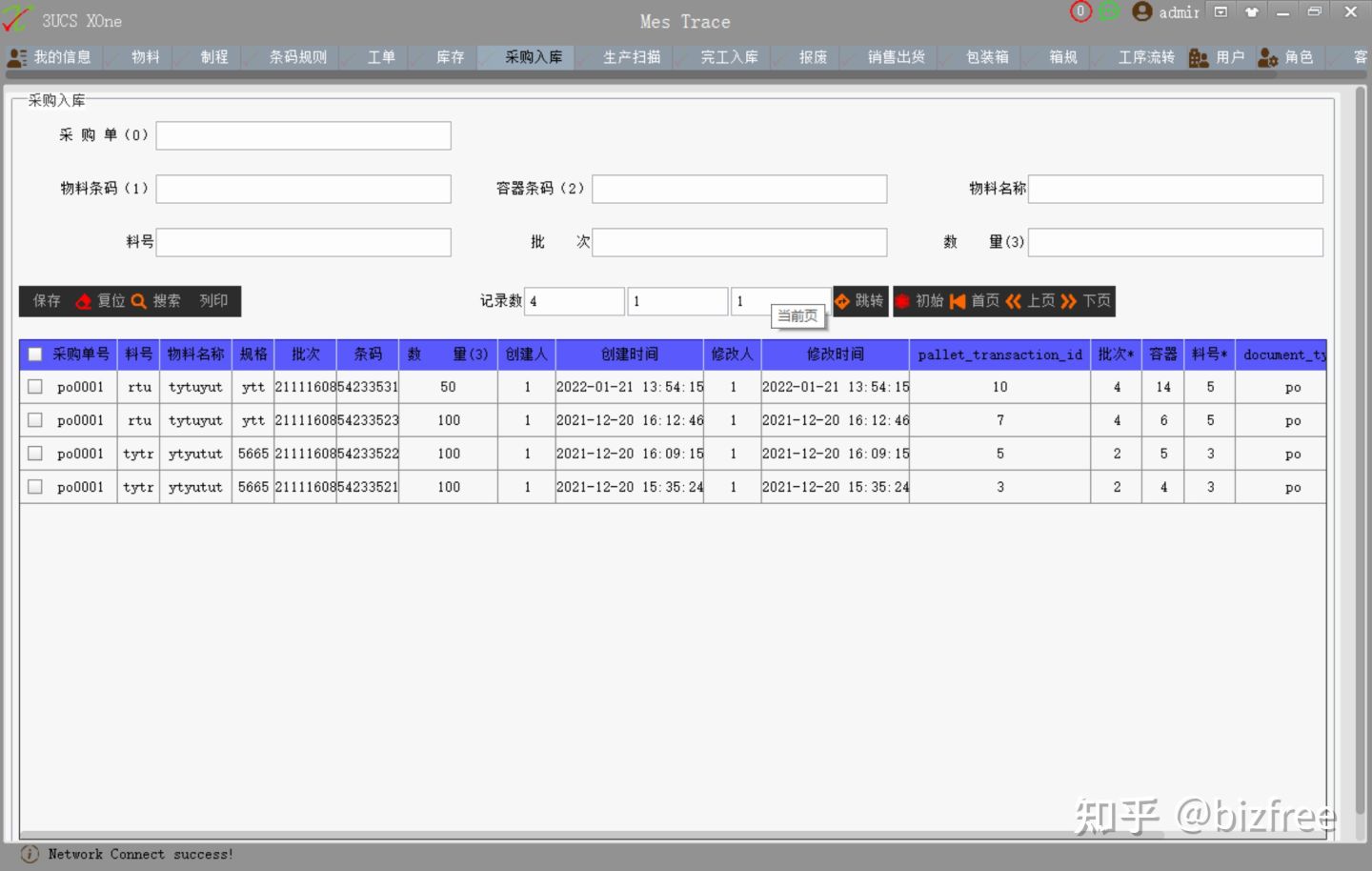
举一个简单的例子，贵司作为供应商向客户提供零部件，而没有下图类似的品质跟踪系统，你可能都无法交货，而这是客户产品质量追踪的一部分，是数字供应链的一部分，你不能独立存在，你必须融入，你不做数字化，你连供应商都不是。这也是数字化的一个很小的部分.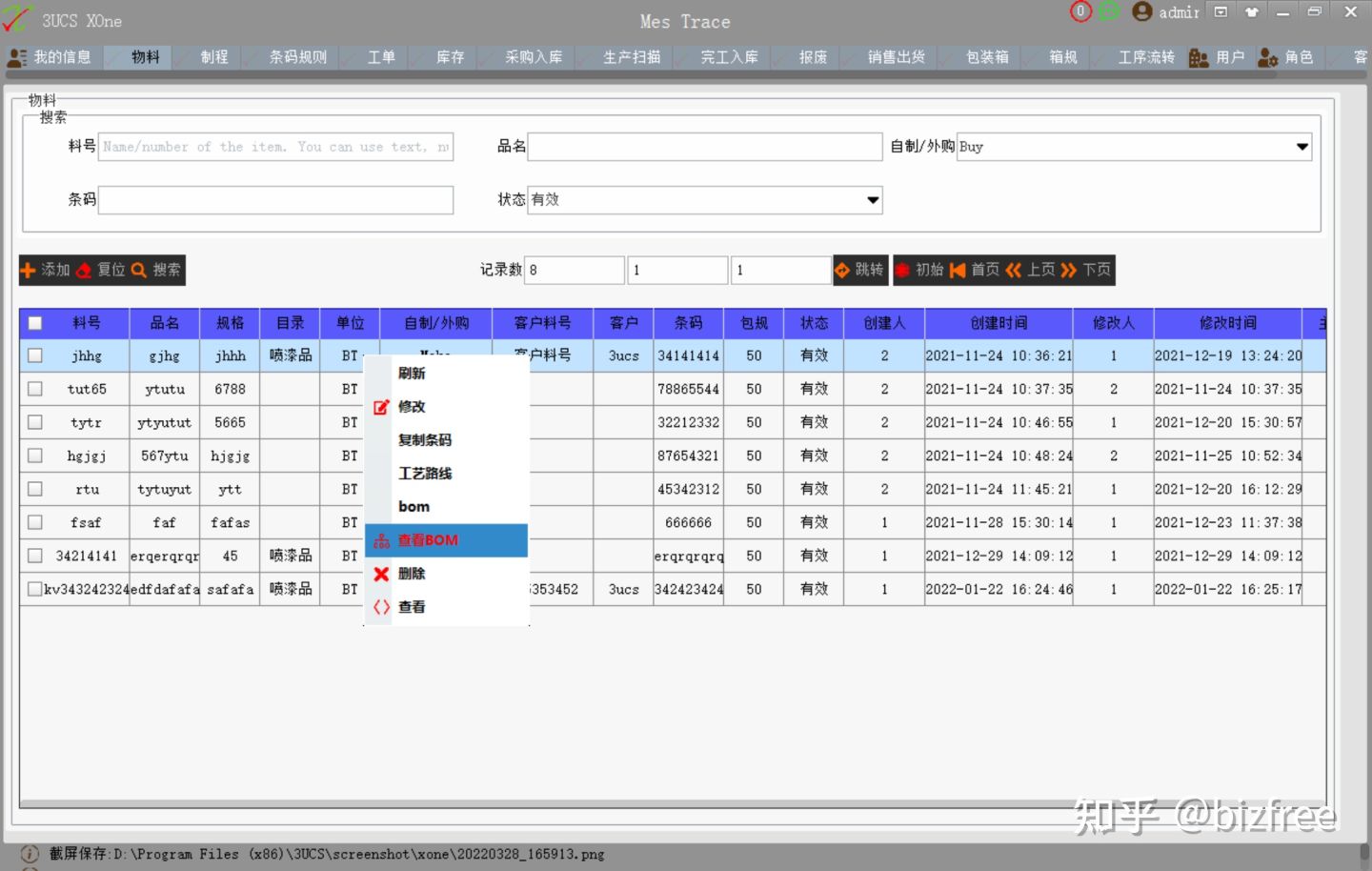

3UCS MES TRACE PC
 
3UCS MES TRACE PC 采购入库

3UCS MES TRACE Android(手机）采购入库
3UCS MES TRACE Android(手机）生产扫描

3UCS MES TRACE Android(手机）完工入库
3UCS MES TRACE Android(手机）销售出货
3UCS MES TRACE Android(手机）报废处理

如何理解「数字化是 IT 公司在给传统企业贩卖焦虑」？的更多相关文章

  1. 【入门必看】不理解「对象」？很可能有致命bug：简单的Python例子告诉你

    简介:越来越多的人要在学习工作中用到『编程』这个工具了,其中很大一部分人用的是Python.大部分人只是做做简单的科研计算.绘图.办公自动化或者爬虫,但-- 这就不需要理解「指针与面向对象」了吗? 在 ...

  2. 未来科技城 x 奇点云打造「企业数据大脑」，助力1.3万家企业服务

    “当前,政府数字化和数字政府建设已成为一种趋势.一种必然,并且有了一条水到渠成式的实现路径.” 上升为国家战略的数字中国建设加速了”智慧政务“的生动实践,杭州未来科技城的「企业数据大脑」就是一个典型. ...

  3. 【动画】看动画轻松理解「Trie树」

    Trie树 Trie这个名字取自“retrieval”,检索,因为Trie可以只用一个前缀便可以在一部字典中找到想要的单词. 虽然发音与「Tree」一致,但为了将这种 字典树 与 普通二叉树 以示区别 ...

  4. 《React Native 精解与实战》书籍连载「Node.js 简介与 React Native 开发环境配置」

    此文是我的出版书籍<React Native 精解与实战>连载分享,此书由机械工业出版社出版,书中详解了 React Native 框架底层原理.React Native 组件布局.组件与 ...

  5. 何解決 LinqToExcel 發生「無法載入檔案或組件」問題何解決 LinqToExcel 發生「無法載入檔案或組件」問題

    在自己的主機上透過 Visual Studio 2013 與 IISExpress 開發與測試都還正常,但只要部署到測試機或正式機,就是沒辦法順利執行,卡關許久之後找我協助.我發現錯誤訊息確實很「一般 ...

  6. iOS公司账号($99)/企业账号($299)申请

    公司账号($99)与企业账号($299)申请基本大同小异,最主要的差别就在于入口不一样 一.注册Apple ID 在iOSAppStore个人开发者账号申请中已经介绍过注册App ID的流程,这里不再 ...

  7. 电缆公司如何面对企业改革？MES系统打造智能工厂

    项目背景 目前,“互联网+电缆”正在成为电缆行业发展的主流,作为中国领先的大型电缆企业江苏亨通电力电缆有限公司(简称“亨通电缆”)积极响应国家提出的“中国制造2025”号召,实施MES工程项目,启用智 ...

  8. NOIP模拟测试15「建造城市city（插板法）·轰炸·石头剪刀布」

    建造城市 题解 先思考一个简单问题 10个$toot$ 放进5间房屋,每个房屋至少有1个$toot$,方案数 思考:插板法,$10$个$toot$有$9$个缝隙,$5$间房屋转化为$4$个挡板,放在t ...

  9. NOIP模拟16:「Star Way To Heaven·God Knows·Loost My Music」

    T1:Star Way To Heaven 基本思路:   最小生成树.   假如我们将上边界与下边界看作一个点,然后从上边界经过星星向下边界连边,会发现,他会形成一条线将整个矩形分为左右两个部分. ...

随机推荐

  1. kube-scheduler的调度上下文

    前一章节了解到了kube-scheduler中的概念,该章节则对调度上下文的源码进行分析 Scheduler Scheduler 是整个 kube-scheduler 的一个 structure,提供 ...

  2. [linux] 输入&输出&错误流

    输入&输出&错误流 Linux中有三种标准输入输出,分别是STDIN,STDOUT,STDERR,对应的数字分别是0,1,2. 标准 数字 含义 STDIN 0 标准输入,默认从键盘读 ...

  3. 求广义表深度（严5.30）--------西工大noj

    #include <stdio.h> #include <stdlib.h> #include <string.h> typedef enum{ATOM, LIST ...

  4. 基于ABP实现DDD--实体创建和更新

      本文主要介绍了通过构造函数和领域服务创建实体2种方式,后者多用于在创建实体时需要其它业务规则检测的场景.最后介绍了在应用服务层中如何进行实体的更新操作. 一.通过构造函数创建实体 假如Issue的 ...

  5. 基于gitlab 15.1 pages 搭建内部博客一定行版本

    背景 基于 gitlab 15.1版 pages 搭建内部博客,参考官方文档,遇到一个又一个坑.之前看到别人吐槽说 gitlab 官方文档很差,我算是理解了.下面一个个说. 开始 按照官方文档的说法, ...

  6. Spring源码学习笔记9——构造器注入及其循环依赖

    Spring源码学习笔记9--构造器注入及其循环依赖 一丶前言 前面我们分析了spring基于字段的和基于set方法注入的原理,但是没有分析第二常用的注入方式(构造器注入)(第一常用字段注入),并且在 ...

  7. 在django中前后端传输数据的编码格式（contentType）

    写在前面 在django中,针对前后端传输数据的编码格式,我们主要研究的是post请求:因为get请求传输的数据往往是直接放在url的后面的!如: url?username=zhang&pas ...

  8. LuoguP3690 【模板】Link Cut Tree （LCT）

    勉强算是结了个大坑吧或者才开始 #include <cstdio> #include <iostream> #include <cstring> #include ...

  9. git使用的一些坑和新得（一）

    这是一个坑 你要知道作为一个新手对git的使用还处于摸索状态 今天就将这样的坑分享给大家 昨天,接到任务将代码发到远程仓库里.于是,我就天真的按步骤提交了! 然后就: To https: ! [rej ...

  10. Spring的俩大核心概念：IOC、AOP

    1.Spring 有两个核心部分: IOC 和 Aop (1)IOC:控制反转,把创建对象过程交给 Spring 进行管理   (2)Aop:面向切面,不修改源代码进行功能增强 2.Spring 特点 ...