【转载】ArcBall二维控制三维旋转

原文：http://oviliazhang.diandian.com/post/2012-05-19/40027878859

由于目前大多的显示器是二维的，要控制三维物体的旋转就显得不那么直接了。ArcBall是一种将二维鼠标位置的变化映射到三维物体旋转的方法，让用户通过很直观的方法控制物体旋转。

网上相关方法还是不少的，包括：

http://rainwarrior.thenoos.net/dragon/arcball.html

http://nehe.gamedev.net/tutorial/arcball_rotation/19003/

当然，Nehe的例子还是一如既往地很难看懂，总觉得搞竞赛啊算法很好的人代码可读性太差了，可能是追求敲代码的效率吧，苦了读者了。

我觉得说得最清楚的是这个http://en.wikibooks.org/wiki/OpenGL_Programming/Modern_OpenGL_Tutorial_Arcball

下面从头说一下ArcBall的思想。

一言以蔽之，就是把屏幕看成一个球，拖动鼠标就是在转动这个球。

对照http://en.wikibooks.org/wiki/OpenGL_Programming/Modern_OpenGL_Tutorial_Arcball的四个步骤：

1. 首先把按下鼠标和拖动鼠标的坐标记为Q1，Q2，x和y分别按屏幕大小缩放到[-1, 1]。如：Q1(100, 500), Q2(800, 600)，屏幕大小1000x800。则缩放后得到的P1(-0.8, -0.25), P2(0.6, -0.5)。之所以做这个映射完全是为了方便以后的计算，就是Nehe说的Happy Coinsidence~

C++语言: 高亮代码由发芽网提供 // map (x, y) to [-1.0, 1.0] 
vec . x = 2.0 * x / width - 1.0; 
// y is set to be opposite since the coordinates of screen and 
// opengl are different 
vec . y = 1.0 - 2.0 * y / height;

2. 把二维坐标转成三维的，这部是最关键的。现在我们可以把屏幕看成一个xyz都是[-1, 1]的球体了，球心在(0, 0, 0)处。

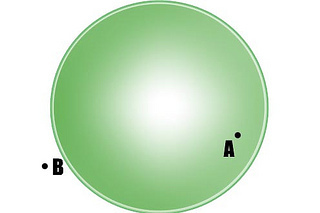
比如A和B是两个鼠标映射后的点，从前视图看，A在球“上”（这里正确的理解是球壳上，而不是球体内部）；B在球体外部。之所以说A在球壳上，是我们人为假设的，就是为了要对应到球体的转动。既然A在球壳上，我们就根据x，y值求的对应的z值（x、y、z的平方和是1，因为在球壳上）；对B而言，我们把它“就近迁移”到球壳上，那么球壳上离B最近的点是什么呢？从正视图看应该是这样的：

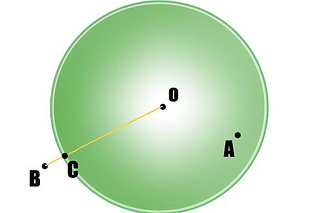
所以我们认为C点的z坐标是0。

所以三维坐标的计算方法：

C++语言: 高亮代码由发芽网提供 double square = vec . x * vec . x + vec . y * vec . y; 
if ( square <= 1.0) { 
    // if (x, y) is within the circle of radius 1 
    // calculate z so that the modulus of vector is 1 
    vec . z = qSqrt( 1.0 - square); 
} else { 
    // if is out of the circle, do nomarlization 
    // this vector is the nearest position on the circle 
    // so that z is 0 
    double length = qSqrt( square); 
    vec . x /= length; 
    vec . y /= length; 
    vec . z = 0.0; 
}

3. 接下来求旋转角。我们知道向量A点乘向量B=|A||B|cos(alpha)其中alpha是向量夹角。根据前两步，我们能得到鼠标按下的位置A和拖动时当前位置在球上的坐标B，现在我们想求出向量OA和OB的夹角。那么Happy Coinsidence就来了，因为球的半径是1，所以|OA|=|OB|=1。那么alpha=arccos(A和B的点积)。

C++语言: 高亮代码由发芽网提供 double ArcBall :: getRotateAngle( Vector3d vec1 , Vector3d vec2) 
{ 
    return qAcos( vec1 . dotProduct( vec2)); 
}

4. 我们知道glRotatex需要三个参数：一个旋转角和一个旋转轴对应的三个坐标。所以接下去我们就要求旋转轴。既然刚刚点积发挥过作用了，这次我们就要让叉乘出出风头了。向量A和B叉乘的结果是它们所在平面的法向量，也就意味着就是我们要求的旋转轴了。

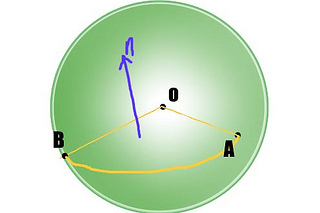
有了旋转角和旋转轴，是不是glRotatex一下就解决了？

但是由于我们只计算了鼠标按下的位置和当前鼠标位置的旋转效果，所以上一次旋转的效果在第二次按下鼠标时就消失了。记录下每次的旋转角和旋转轴显然不是一个好办法，因为旋转次数多了以后每帧都要调用非常多的glRotatex显然不合适。所以我们记录下每次旋转的旋转矩阵，然后利用矩阵乘法达到累积旋转的效果。

已知旋转角和旋转轴求旋转矩阵的方法是：http://en.wikipedia.org/wiki/Rotation_matrix#Rotation_matrix_from_axis_and_angle

网上也有很多别的地方有这个公式，但是实际的效果却是翻转的，我百思不得其解，今天试了一下把这个矩阵转置一下，竟然对了，但是不知道是什么原因，是不是右手系的关系。

到这里，我们就解决用ArcBall二维控制三维旋转了。

下面来说一说几个记录旋转量不同的方法：

1.旋转角和旋转轴：绕某个轴旋转某个角度

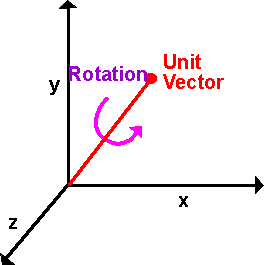
旋转矩阵：

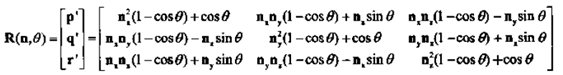
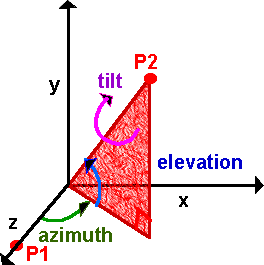
2.欧拉角：分别绕三轴旋转的角度，注意是绕轴三次旋转，而不是一次。就好像在说，先绕y轴转30度，再绕x轴旋转20度，再绕z轴旋转50度。用glRotatex的话，需要用三次。旋转的顺序也是有关的，而且万一选择不好，会造成万向锁现象。

旋转矩阵：

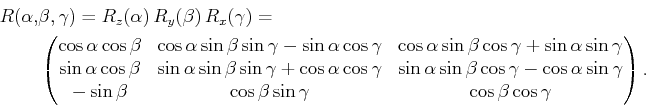
3. 至于四元数，我自己也没搞清楚，就不瞎掰了……