第一步：输入目标条件和约束条件。每行以分号隔开。然后点击工具栏上的Solve按钮，或Lingo菜单下的Solve子菜单。

第二步：检查report中的结果。

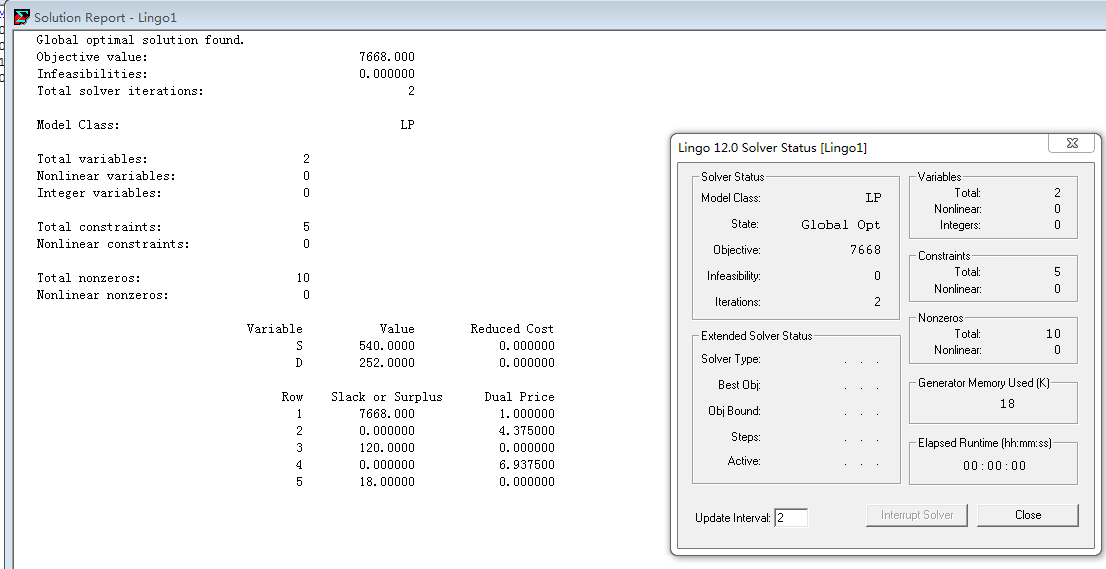
默认情况下，Lingo不进行灵敏度分析。

需要在Lingo中一下配置才可以生成灵敏度分析报告：Lingo菜单》Options. General Solver选项卡》Dual Computations:Prices and Ranges. 然后点击Apply按钮。

重新点击Solve菜单和Range菜单以生成如下灵敏度分析报告（Range Report）

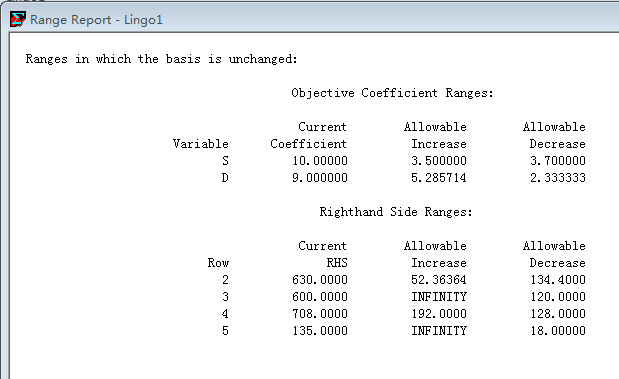
用Lingo求解线性规划问题的更多相关文章

  1. Lingo求解线性规划案例4——下料问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 造纸厂接到定单,所需卷纸的宽度和长度如表 卷纸的宽度 长度 5 7 9 10000 30000 20000 工 ...

  2. Lingo求解线性规划案例1——生产计划问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 说明: Lingo版本:                            某工厂明年根据合同,每个季度末 ...

  3. Lingo求解线性规划案例3——混料问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/  某糖果厂用原料A.B和C按不向比率混合加工而成甲.乙.丙三种糖果(假设混合加工中不损耗原料).原料A.B.C ...

  4. Lingo求解线性规划案例2——多阶段投资问题

     凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 某公司现有资金30万元可用于投资,5年内有下列方案可供采纳:   1号方案:在年初投资1元,2年后可收回1. ...

  5. 图论中最优树问题的LINGO求解

    树:连通且不含圈的无向图称为树.常用T表示.树中的边称为树枝,树中度为1的顶点称为树叶. 生成树:若T是包含图G的全部顶点的子图,它又是树,则称T是G的生成树. 最小生成树:设T=(V,E1)是赋权图 ...

  6. matlab学习笔记之求解线性规划问题和二次型问题

    一.线性规划问题 已知目标函数和约束条件均为线性函数,求目标函数的最小值(最优值)问题. 1.求解方式:用linprog函数求解 2.linprog函数使用形式: x=linprog(f,A,b)  ...

  7. matlab 求解线性规划问题

    线性规划 LP(Linear programming,线性规划)是一种优化方法,在优化问题中目标函数和约束函数均为向量变量的线性函数,LP问题可描述为: minf(x):待最小化的目标函数(如果问题本 ...

  8. Python求解线性规划——PuLP使用教程

    简洁是智慧的灵魂,冗长是肤浅的藻饰.--莎士比亚<哈姆雷特> 1 PuLP 库的安装 如果您使用的是 Anaconda[1] 的话(事实上我也更推荐这样做),需要先激活你想要安装的虚拟环境 ...

  9. 单纯形求解线性规划(BZOJ1061)

    推荐一篇论文:http://wenku.baidu.com/view/ce5784754a7302768f99391d 我们设xi为第i个志愿者的招募次数,以样例为例,则不难列出如下的线性规划方程: ...

随机推荐

  1. 2018.09.23 codeforces 1053B. Vasya and Good Sequences（前缀和）

    传送门 考试的时候卡了一会儿. 显然这个答案只跟二进制位为1的数量有关. 还有一个显然的结论. 对于一个区间[l,r][l,r][l,r],如果其中单个数二进制位为1的数量最大值不到区间所有数二进制位 ...

  2. 2018.08.17 洛谷[POI2010]GRA-The Minima Game（线性dp）

    传送门 短代码神奇dp. 自己yy的思路居然1A了好高兴啊! 不难想到每个人选择的时候一定是取连续的最大的那一段数,自然需要先排序. 然后可以用dp[i]表示当前最大数是a[i]的时候先手可以获得的最 ...

  3. yii2 控制器的生命周期

    控制器生命周期 http://www.yii-china.com/doc/guide/structure_controllers.html 处理一个请求时,应用主体 会根据请求路由创建一个控制器,控制 ...

  4. hdu-1060（数学问题）

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1061 思路:结论:a=10^(N*lg(N) - [lg(N^N)]); 证明:如果一直a是结果,则a ...

  5. Django入门指南-第9章：静态文件设置（完结）

    http://127.0.0.1:8000 #下一步是告诉Django在哪里可以找到静态文件.打开settings.py,拉到文件的底部,在STATIC_URL后面添加以下内容: STATICFILE ...

  6. EXT combobox 二级连动 清空store缓存数据

    项目中有这样的一个需求,做一个连动操作,如图: 所属行业中的combobox中下拉框中的值会根据前一个选择框中的值动态去变化,这个其实非常好做,但不是我现在讨论的主要问题,主要问题是,当第二次选择了& ...

  7. web大文件上传(web应用---SSH框架)

    版权所有 2009-2018荆门泽优软件有限公司 保留所有权利 官方网站:http://www.ncmem.com/ 产品首页:http://www.ncmem.com/webapp/up6.2/in ...

  8. 201709012工作日记--一台电脑创建两个Github账户上传代码

    1. 在一台主机上面使用多个GitHub账号 有时候,我们需要将个人账号和公司账号区分,这时候我们就会需要在一台电脑上使用2个不同的git账号. 2. 上传文件 http://blog.csdn.ne ...

  9. day05(Object,tostring(),equals(),System,Date,SimpleDateFormat,拆装箱，正则表达式)

    Object类, 是所应类的父类: 拥有自己的方法:常用的    红颜色标记的为常用的方法 toString() 用法:打印对象的地址值 getClass() 获取当前类的字节码文件getName() ...

  10. 如何利用Visio设计一个系统的结构图

    首先建立一个空的vison列表 添加图形和连接线 托选一个矩形块到操作台上,并进行底色填充 选择有向线段1拖到矩形模块上,此时有向线段1会自动吸附到矩形的中点处. 此时按下图操作即可取消,自动吸附 托 ...