AtCoder | ARC102 | 瞎讲报告

目录

• ARC102
  • 前言
  • 正文

传送链接~

ARC102

前言

实在是太菜了。。。。写完第一题就弃疗。。感觉T3好歹也是道可做题吧！！然后T2怎么又是进制拆分！

正文

A

• 题意 给你两个数字\(n,k(1 \leq n,k \leq 2e5)\) 求出有序对\((a,b,c)\) 的数量 使得满足\((a,b,c \leq n)\) 且 \(a+b , a+c , b+c\) 都是\(k\)的倍数

• 题解 可以很快地发现 \(a mod k == b mod k == c mod k\) 且 \((a+b) mod k == 0\) 那么\(a,b,c\) 模 \(k\) 之后的情况只剩下了两种
  • 都等于0
  • 都等于 \(\frac{k}{2}\)

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=1e5+10;
int yz[N];

int main(){
    int n,k;scanf("%d%d",&n,&k);
    LL ans=0;
    LL gg=n/k;
    ans=gg*gg*gg;
    if(k%2==0){
        LL pos=n/k;
        if(pos*k+(k/2)<=n) pos++;
        ans+=pos*pos*pos;
    }
    printf("%lld\n",ans);
    return 0;
}

B

• 题意 给你一个数\(L(2 \leq L \leq 1e6)\) 让你构造出一张有向图 最多20个点 60条边 （顶点按照1，2，...标号 且满足拓扑序为 1,2,3....

• 题解 看到最多20个点很明显可以想到二进制拆分嘛！！
  首先我们可以构造出这么一张图 ：：
  
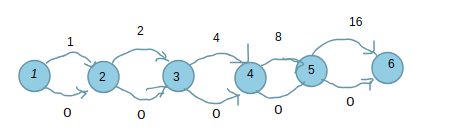
  然后我们拆分一下\(L\) 我们对于剩下的 可以钦定高位 让低位从\(0000..\)一直取到\(1111...\)
  

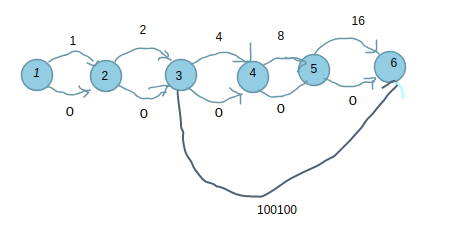
#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=30;
struct data{
    int nt,to,w;
}a[N*N];
int b[N],head[N];
int n,m,cnt=0;

void add(int x,int y,int w){
    a[++cnt].to=y,a[cnt].w=w,a[cnt].nt=head[x],head[x]=cnt;
}

int main(){
    int L;scanf("%d",&L);
    int n=0,tmp=L;
    for(;L;L>>=1) n++;
    L=tmp;
    fr(i,1,n-1) add(i,i+1,1<<(i-1)),add(i,i+1,0);
    int gg=1<<(n-1);
    rf(i,n-1,1) if((L>>(i-1))&1) add(i,n,gg),gg+=(1<<(i-1));
    printf("%d %d\n",n,cnt);
    fr(u,1,n) for(int i=head[u];i;i=a[i].nt){
        printf("%d %d %d\n",u,a[i].to,a[i].w);
    }
    return 0;
}

C

• 题意 给你\(n\)个骰子 每个骰子有\(k\)个面 代表的数字分别为\(1...k\) 骰子相同 对于每一个\(2 \leq i \leq 2*k\) 问有多少钟方案使得任意两个骰子相加和不为\(i\)
  \(n,k \leq 2000\)

• 题解 组合数学 容斥
  我们考虑对于一个\(i\) 有多少对是不合法的 设为\(t\)
  那么我们可以进行容斥操作。。 枚举\(j\)对不合法的
  那么对于剩下的\(n-2*j\)个骰子 随意投 又骰子是相同的 等价于一个放球问题 \(n-2*j\)个相同的球放入\(k\)个盒子里 可以为空
  \(C_{n-2*j+k-1}^{k-1}\)

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=4010,mod=998244353;
LL jc[N]={1},ny[N];

void Mul(LL &x,LL y){
    x=(x*y)%mod;
}

void Add(LL &x,LL y){
    x=(x+y+mod)%mod;
}

LL mul(LL x,LL y){
    return x*y%mod;
}

LL q_pow(LL x,int y=mod-2){
    LL ans=1;
    for(;y;y>>=1){
        if(y&1) Mul(ans,x);
        Mul(x,x);
    }
    return ans;
}

LL C(int x,int y){
    if(x==y||!y) return 1;
    LL pos=mul(jc[x],mul(ny[y],ny[x-y]));
    //printf("%d %d %lld\n",x,y,pos);
    return pos;
}

int main(){
    int n,k;scanf("%d%d",&k,&n);
    fr(i,1,n+k) jc[i]=jc[i-1]*1LL*i%mod,ny[i]=q_pow(jc[i]);
    fr(i,2,2*k){
        int gg=i/2;
        if(i-i/2>k) gg=0;
        else if(i>k+1) gg-=(i-k-1);
        LL ans=0;
        //printf("zz%d %d\n",i,gg);
        fr(j,0,gg) {
            if(j*2>n) break;
            //printf("j=%d gg=%d n-2*j+k-1=%d k-1=%d\n",j,gg,n-2*j+k-1,k-1);
            LL pos=mul(C(gg,j),C(n-2*j+k-1,k-1));
            if(j&1) Add(ans,-pos);
            else Add(ans,pos);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

D

• 题意 给出一个\(n\)的排列 每次可以交换这个三个数\(a_{i-1},a{i},a_{i+1}\) 满足\(a_{i-1} > a_i > a_{i+1}\) 则交换\(a_{i-1}\)和\(a_{i+1}\) 问最后能否将原序列变成\(1,2,3,4...n\)

• 题解 首先搞出\(b[]\) \(b[i]=(a[i]==i)\)
  - 如果有连续三个\(b\)是0的话显然是不可行的
  - 将\(b\)数组划分成一段一段
  对于\([l,r]\)这一段 \(a[l]至a[r]\) 的值域也必须是\([l,r]\)
  考虑\(a[i]>i\) 就看离\(a[i]\)最近的\(a[j]>i\) 之中的\(a[j]\)是否大于\(a[i]\)
  \(a[i]<i\) 同理

#include<bits/stdc++.h>
#define fr(i,x,y) for(int i=x;i<=y;++i)
#define rf(i,x,y) for(int i=x;i>=y;--i)
#define LL long long
using namespace std;
const int N=3e5+10;
int a[N],b[N];

void fail(){
    printf("No\n");
    exit(0);
}

bool check(int l,int r){
    int L=0,R=0;
    fr(i,l,r){
        if(b[i]<l||b[i]>r) return false;
        if(b[i]<i)
            if(L>b[i]) return false;
             else L=b[i];
        else if(b[i]>i)
            if(R>b[i]) return false;
             else R=b[i];
    }
    return true;
}

int main(){
    int n;scanf("%d",&n);
    fr(i,1,n) scanf("%d",&b[i]),a[i]=(b[i]==i);
    fr(i,2,n-1) if(!a[i-1]&&!a[i]&&!a[i+1]) fail();
    fr(i,1,n){
        if(!a[i]){
            int l=i,r=i,nw=0;
            while((a[r+1]^nw)&&r+1<=n) r++,nw^=1;
            //printf("%d %d\n",l,r);
            if(!check(l,r)) fail();
            i=r;
        }
    }
    printf("Yes\n");
    return 0;
}