【Openxml】将Openxml的椭圆弧线arcTo转为Svg的椭圆弧线

本文将介绍如何将OpenXml的actTo转为Svg的弧线(a)

OpenXml的artTo

首先下面是一段OpenXml的arcTo弧线

<arcTo wR="152403" hR="152403" stAng="cd4" swAng="-5400000" />

假设我们当前的点是(0,0)，这时候我们已知的信息如下：

当前点坐标：（x1,y1)=(0,0)
椭圆的半径：半长轴 rx=wR=152403，半短轴 ry=hR=152403
起始角到结束角的夹角：起始角θ1=stAng=cd4，夹角Δθ=swAng,结束角θ2=θ1+Δθ
是否优(大)弧：fA=|Δθ|>Π(180°)
顺逆时针：fS=|Δθ|>0°

目前Svg的椭圆弧线参数字符串为以下：

a  rx  ry  x-axis-rotation  large-arc-flag  sweep-flag  x  y

其中涉及到的参数：

参数	说明	备注
rx	椭圆半长轴	已知：rx=wR=152403
ry	椭圆半短轴	已知：ry=hR=152403
x-axis-rotation	椭圆相对于坐标系的旋转角度，角度数而非弧度数	已知：0
large-arc-flag	是否优(大)弧：0否，1是	已知：fA=\|Δθ\|>Π(180°)
sweep-flag	绘制方向：0逆时针，1顺时针	已知：fS=\|Δθ\|>0°
x	圆弧终点的x坐标	未知
y	圆弧终点的y坐标	未知

因此实际上，我们需要求出的则是圆弧终点坐标就能够完成最终换算到Svg椭圆弧线字符串了

求椭圆弧上任意一点的二维矩阵方程式

以下是我从W3C的SVG官方文档中获取到的关于椭圆任意一点的二维矩阵方程式：

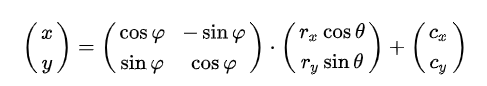
因此的存在以下两个(开始点和终点)椭圆任意一点的二维矩阵方程式：

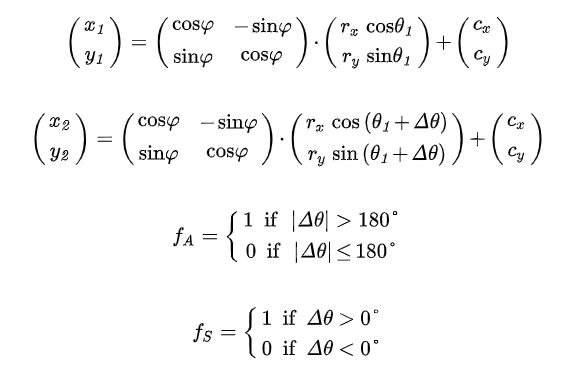
其中涉及到的参数：

参数	说明	备注
(x1,y1)	当前坐标	已知：(0,0)
(x2,y2)	终点坐标	未知
φ	椭圆相对于坐标系的旋转角度	已知：0°
θ1	起始角	已知：stAng
Δθ	起始角到结束角的夹角	已知：swAng
(cx,cy)	椭圆中心坐标点	未知
fA	是否优(大)弧	已知：fA=\|Δθ\|>Π(180°)
fS	绘制方向	已知：fS=Δθ>0°

因此推导公式如下:

步骤1：

因为开始点的椭圆任意一点的二维矩阵方程式为

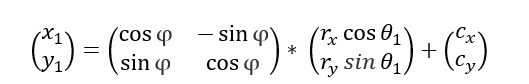
所以能够得出两行一列矩阵CxCy为：

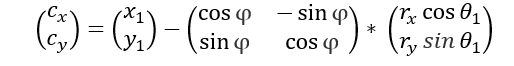
步骤2：

因为终点的椭圆任意一点的二维矩阵方程式为

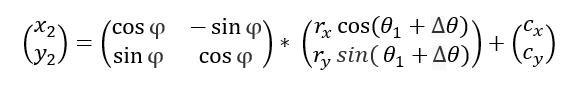
因此将矩阵CxCy带入到终点点的椭圆任意一点的二维矩阵方程式：

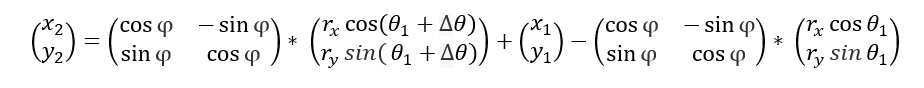
代码部分

在写代码之前，我们需要安装一些所需要用到的库，Openxml单位换算为Pixel的库和矩阵运算用到的库：

通过nuget包的控制台执行以下命令：

Openxml单位换算库

Install-Package dotnetCampus.OpenXmlUnitConverter -Version 1.5.1

矩阵运算库

Install-Package MathNet.Numerics -Version 5.0.0-alpha02

然后正式开始我们的代码,我们通过WPF应用窗体来展示效果：

前端xaml代码：

<Window x:Class="OpenxmlActToSvgSample.MainWindow"

        xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"

        xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"

        xmlns:d="http://schemas.microsoft.com/expression/blend/2008"

        xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"

        xmlns:local="clr-namespace:OpenxmlActToSvgSample"

        mc:Ignorable="d"

        Title="MainWindow" Height="450" Width="800">

    <Grid>

        <Path x:Name="Path" Stroke="Blue" HorizontalAlignment="Center" VerticalAlignment="Center"/>

    </Grid>

</Window>

后端cs代码：

        public MainWindow()

        {

            InitializeComponent();

            //Openxml的360° circle

            const double c = 21600000d;

            //circle divide 4

            var cd4 = c / 4;

            //<arcTo wR="152403" hR="152403" stAng="cd4" swAng="-5400000" />

            var wR = 152403;

            var hR = 152403;

            var stAng = cd4;

            var swAng = -5400000d;

            StringBuilder stringPath=new StringBuilder();

            var currentPoint=new Point(0, 0);

            stringPath.Append($"M {currentPoint.X} {currentPoint.Y}");

            ParseOpenxmlArcTo(stringPath, wR, hR, stAng, swAng, currentPoint);

            this.Path.Data=Geometry.Parse(stringPath.ToString());

        }

         private Point  ParseOpenxmlArcTo(StringBuilder stringPath, double wR, double hR, double stAng, double swAng, Point currentPoint)

        {

            const string comma = ",";

            //将Openxml的角度转为真实的角度

            var θ1 = new Angle((int)stAng).ToRadiansValue();

            var Δθ = new Angle((int)swAng).ToRadiansValue();

            //旋转角

            var φ = 0d;

            //是否是大弧

            var isLargeArcFlag = Math.Abs(Δθ) > Math.PI;

            //是否是顺时针

            var isClockwise = Δθ > 0;

            var rx = new Emu(wR).ToPixel().Value;

            var ry = new Emu(hR).ToPixel().Value;

            //获取终点坐标

            var pt = GetArBitraryPoint(rx, ry, swAng, stAng, φ, currentPoint);

            currentPoint = pt;

            // 格式如下

            // A rx ry x-axis-rotation large-arc-flag sweep-flag x y

            // 这里 large-arc-flag 是 1 和 0 表示

            stringPath.Append("A")

                   .Append(rx) //rx

                   .Append(comma)

                   .Append(ry) //ry

                   .Append(comma)

                   .Append(φ) // x-axis-rotation

                   .Append(comma)

                   .Append(isLargeArcFlag ? "1" : "0") //large-arc-flag

                   .Append(comma)

                   .Append(isClockwise ? "1" : "0") // sweep-flag

                   .Append(comma)

                   .Append(pt.X)

                   .Append(comma)

                   .Append(pt.Y)

                   .Append(' ');

            return currentPoint;

        }

         /// <summary>

        /// 获取椭圆任意一点坐标

        /// </summary>

        /// <returns></returns>

        private static Point GetArBitraryPoint(double rx, double ry, double Δθ, double θ1, double φ, Point currentPoint)

        {

            //开始点的椭圆任意一点的二维矩阵方程式

            var matrixX1Y1 = DenseMatrix.OfArray(new double[2, 1]

            {

                { currentPoint.X},

                { currentPoint.Y}

            });

            var matrix1 = DenseMatrix.OfArray(new double[2, 2]

            {

            { Math.Cos(φ),-Math.Sin(φ)},

            { Math.Sin(φ),Math.Cos(φ)}

            });

            var matrix2 = DenseMatrix.OfArray(new double[2, 1]

            {

                { rx*Math.Cos(θ1)},

                { ry*Math.Sin(θ1)}

            });

            var matrixCxCy = matrixX1Y1 - (matrix1 * matrix2);

            //终点的椭圆任意一点的二维矩阵方程式

            var matrix3 = DenseMatrix.OfArray(new double[2, 1]

            {

                { rx*Math.Cos(θ1+Δθ)},

                { ry*Math.Sin(θ1+Δθ)}

            });

            var matrixX2Y2 = matrix1 * matrix3 + matrixCxCy;

            return new Point(matrixX2Y2.Values[0], matrixX2Y2.Values[1]);

        }

效果如下：

可以看到，我们成功的绘制出我们的一条椭圆弧线，虽然很简单，但是其实这条弧线是我取ppt形状缺角矩形当中的一条弧线，在绘制其形状时候，上述方法会自动根据arcTo的数据来自动判断弧线的大小弧、顺逆时针等情况的绘制

源码

BlogCodeSample/OpenxmlActToSvgSample at main · ZhengDaoWang/BlogCodeSample

参考

Implementation Notes — SVG 2

【OpenXml】Pptx的形状转为WPF的Geometry - RyzenAdorer - 博客园

dotnet OpenXML SDK 形状几何 Geometry 的计算公式含义