带你读AI论文丨用于目标检测的高斯检测框与ProbIoU

摘要：本文解读了《Gaussian Bounding Boxes and Probabilistic Intersection-over-Union for Object Detection》，该论文针对目标检测任务，提出了新的高斯检测框(GBB)，及新的计算目标相似性的方法(ProbIoU)。

本文分享自华为云社区《论文解读系列十九：用于目标检测的高斯检测框与ProbIoU》，作者：BigDragon。

论文地址： https://arxiv.org/abs/2106.06072

Github地址： https://github.com/ProbIOU

现有目标检测的改进方向主要集中在：训练更大数据集 (LVIS dataset)、处理类别不均衡、提出更好的 backbones 、建立长距离相互作用模型 (Transformers ， LambdaNetworks)、分类和检测框的权衡分析，对于检测框的呈现形式相关研究较少。现有目标检测任务中以水平框 (HBB )和旋转框 (OBB )为主，呈现形式还是矩形或者类矩形。而现有目标距离及相似性计算方式包括：IoU (Intersection over Union)、 GIoU (Generalized IoU )、 DIoU (Distance IoU)、 PIoU (Pixel IoU)， Gaussian Wasserstein Distance (GWD)。

现有OBB算法在细长及旋转物体检测问题相对于HBB算法有所提高，但是与目标语义分割的贴合度不高，因此，本文提出更加贴合语义分割形式的分割呈现形式及对应的目标相似度计算方法。

该论文贡献如下：

提出一种新的椭圆形目标检测框 (Gaussian Bounding Boxes，GBB)

GBB与目标的语义分割mask形状更加接近，更加贴合非矩形目标，在非矩形目标检测效果优于HBB和OBB。

提出一种新的目标相似度的计算方法 (Probabilistic IoU，ProbIoU)

基于Hellinger Distance的ProbIoU，考虑了2D高斯分布的特点，满足所有距离度量标准，能够表示不同分布间的真实距离，且处处可微，能提升OBB和HBB目标检测效果。

1.Gaussian Bounding Boxes (GBB)

为在 2 维区域确定一个二维高斯分布，需要计算其均值μ和协方差矩阵∑，其中μ为 (x0， y0) T，协方差矩阵∑可通过下列公式进行计算。在目标检测任务中，可直接设置（x0，y0，a，b，c ）作为目标检测中的回归任务中的参数，也可将回归任务中参数表示为（x0， y0，a ’，b ’，θ )，而后者的形式更加符合现有旋转检测框的输出形式。

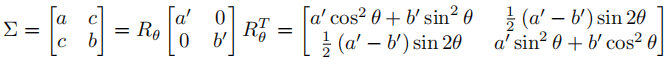
假设

水平框及旋转框向高斯框转换中遵循以下假设：目标区域为 2 维二元区域 Ω，且 Ω 符合均匀概率分布，则该分布的均值 μ 和协方差矩阵 ∑ 可通过如下公式进行计算。

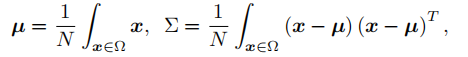
其中， N 表示区域 Ω 的面积。

1.1 将 HBB 转化为 GBB

对于 HBB ，其二元区域 Ω 为以 (x0， y0) 为中心，高为 H，宽为 W 的矩形区域 , 因此 μ 为 (x0， y0) , 它的协方差矩阵 Σ 可通过如下公式进行计算

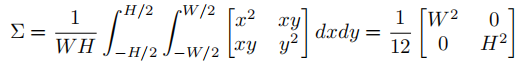
因此，可以得出 a=w²/ 12 ， b =H²/12，c=0 。如上述公式所示，转换后的高斯框也可以转化水平框，该过程是可逆的。

1.2 将 OBB 转化为 GBB

OBB 转化为 GBB 需要计算 (a ’，b ’，θ)，如下图所示，方差 a ’和b ’ 可通过将旋转框转化为水平框进行计算，其协方差矩阵可通过下列公式进行计算。

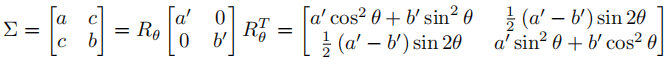
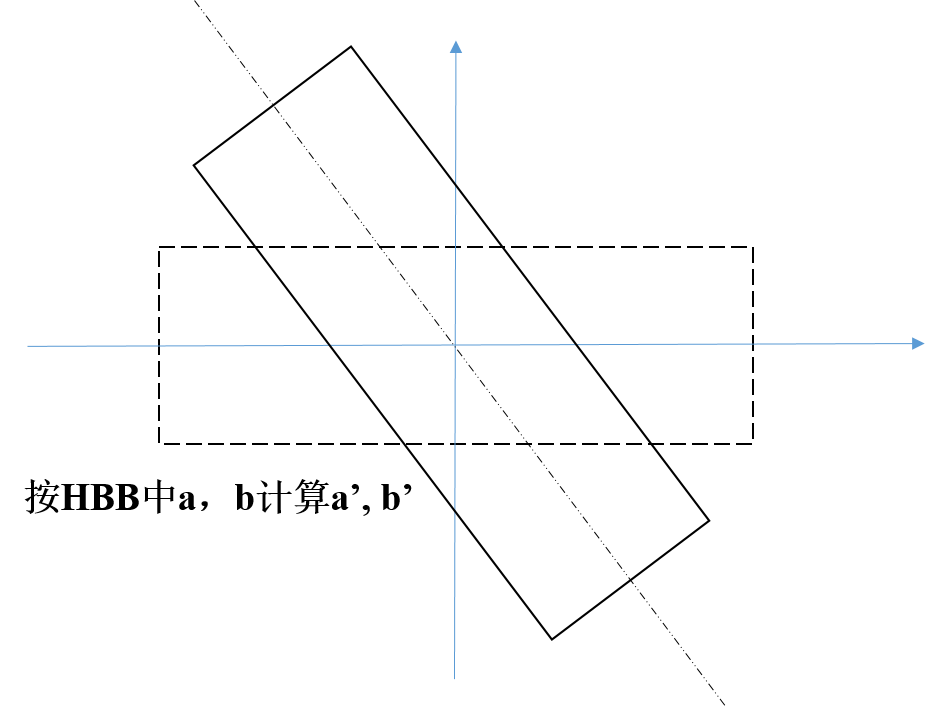
1.3 多边形框 (PBB) 转化为 GBB

多边形框转化为高斯框，可按下列公式进行计算：

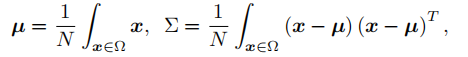
2. ProbIoU 及定位损失函数

2.1 ProbIoU

Bhattacharyya Distance (BD)

为计算不同 GBB 间的相似度，本文首先采用了 Bhattacharyya Coefficient(BC)；两个概率密度函数 p(x)和 q(x) 间的 BC 按下列公式进行计算：

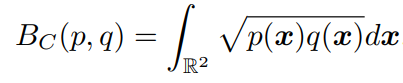
其中 BC (p，q ) ∈ [0，1]，当且仅当两个分布相同时，BC (p，q)=1 。

基于上述 BC ( p，q )，可以得到不同分布间的巴氏距离 (Bhattacharyya Distance, BD), 两个概率密度函数p(x)和q(x) 间的BD按下列公式进行计算：

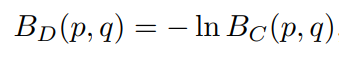
当 p ~N (μ1，Σ1)， q~N (μ2， Σ2 ) 且目标检测中实际问题为2维向量及矩阵，巴氏距离 BD 可通过如下公式进行计算：

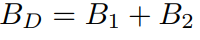
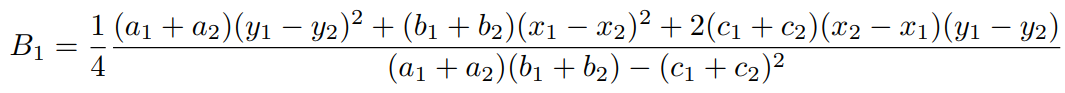
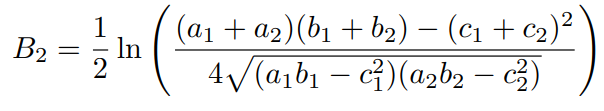
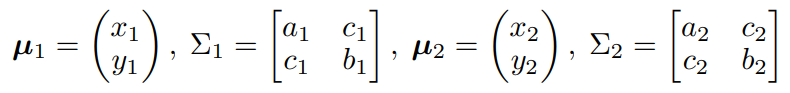
Hellinger Distance (HD)

由于 Bhattacharyya Distance 不满足三角不等式，所以它并不是真实的距离，因此，为表示真实距离，采用 Hellinger Distance (HD) ，其公式如下：

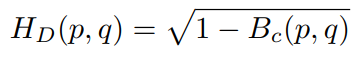
其中 HD (p，q) ∈ [0,1]，当且仅当两个分布相同时， HD(p，q)=0 。

Probabilistic IoU (ProbIoU)

基于上述 Hellinger Distance ，本文提出高斯分布相似性计算方法 ProbIoU ，其具体计算公式如下：

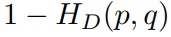
2.2 定位损失函数

假设预测 GBB 为 p= (x1，y1，a1，b1，c1 )，真实 GBB 为 p=(x2，y2，a2，b2，c2 )，则其损失函数如下所示：

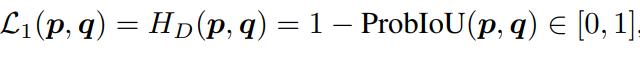
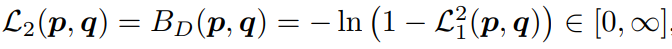
然而，当预测 GBB 远离真实 GBB 距离时， L1 损失函数的值接近于 1 ，训练过程产生梯度小且收敛速度慢。 L2 损失函数避免了上述问题，但与 IoU 的几何关系弱，因此，建议首先采用 L2 损失函数训练，然后切换至 L1 损失函数。

2.3 ProbIoU 的特性

基于 Hellinger Distance 的 ProbIoU 具有以下特性：

三个函数中所有参数都是可微的；
Helinger Distance 满足所有距离度量标准；
损失函数对对象缩放是不变的。

3. 实验结果

3.1 不同检测框实验结果

在 COCO2017 上进行训练，通过对比 GBB 、OBB 、HBB 检测得到的 IoU，可得到如下结论：

GBB 在 COCO 2017 中 77 类别的均值 IoU 要高于 HBB 和 OBB
GBB 在 traffic light 、 microwave 、 tv 三个类别要差于 HBB 和 OBB

3.2 ProbIoU loss 对于 HBB 、 OBB 检测的提升

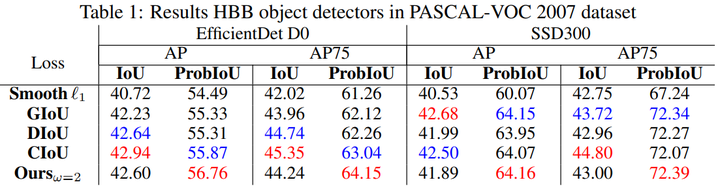
将基于 ProbIoU 的损失函数用于 HBB 检测任务中，分别采用 EfficientDet D0 和 SSD 300 在 PASCAL-VOC 2007 数据集训练。如下表所示，相对于 IoU , 采用 ProbIoU 方法在 AP 及 AP75 均有提升，采用基于 ProbIoU 的损失函数的模型均能达到较高 AP 。

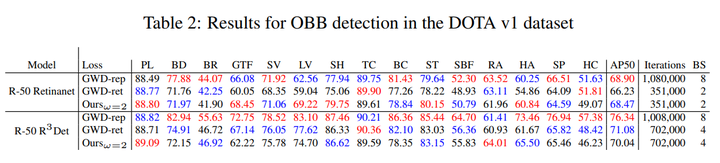
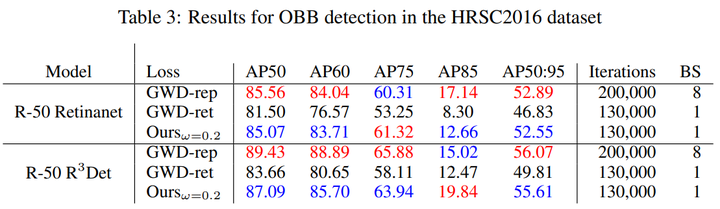
将基于 ProbIoU 的损失函数用于OBB 检测任务中，分别采用 R-50 Retinanet 及 R-50 R3Det ，在 DOTA v1 及 HRSC2016 数据集进行训练。如下表所示，在 DOTA V1 数据集，采用 Retinanet 模型时，基于 ProbIoU 的损失函数 AP 比 GWP-ret 高 2%；采用 R3Det 模型时，其结果与GWD-rep 和GWD-ret 接近。在 HRSC2016 数据集上，基于 ProbIoU 的损失函数结果与GWD-rep 相当，并且优于GWD-ret 。

4. 总结

本文所呈现的方法包含以下三个重要部分：

采用高斯分布形式检测框 (GBB）
提出基于 Hellinger Distance 的 ProbIoU，并提出对应的损失函数 L1，L2
训练过程中，采用L1 和 L2 损失函数组合效果更佳

本文所呈现的方法局限性包含以下两个部分：

对于等轴的高斯分布，无法确定其旋转角度
对于细长目标，训练过程中容易梯度过大，造成训练不稳定。

想了解更多的AI技术干货，欢迎上华为云的AI专区，目前有AI编程Python等六大实战营供大家免费学习

点击关注，第一时间了解华为云新鲜技术~