数值计算：Legendre多项式

Legendre多项式的概念以及正交特性在此不多作描述，可以参考数学物理方程相关教材，本文主要讨论在数值计算中对于Legendre多项式以及其导数的计算方法。

Legendre多项式的计算

递推公式

\[\begin{align}
(n+1)P_{n+1}(x)=(2n+1)x \cdot P_{n}(x)-nP_{n-1}(x) \qquad (n\ge2)
\end{align}
\]

通式可以用幂级数表示为以下形式：

\[\begin{align}
P_{n}(x)=\sum\limits_{k=0}^{[\frac{n}{2}]}{\frac{(-1)^k(2n-2k)!}{2^nk!(n-k)!(n-2k)!}}x^{n-2k} \qquad n=0,1,2,\cdots
\end{align}
\]

Legendre多项式前几项

\(n\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(P_{n}(x)\)	\(1\)	\(x\)	\(\frac{1}{2}(3x^2-1)\)	\(\frac{1}{2}(5x^3-3x)\)	\(\frac{1}{8}(35x^4-30x^2+3)\)​

---

在实际数值计算中，按照通项公式计算\(P_n(x)\)​​会涉及到大量的乘除法运算，同时由于数据字节长度的限制，对于基数较大阶乘的运算会导致数据的溢出，因此，在实际的计算中，使用递推公式计算\(P_n(x)\)​​更为合适。

%% Legendre多项式Pi(x)
function L=myLegendre(N,x)
% 返回Pi(x),i=0~N ，x为标量
if N<2
    error("N is less then 2 !")
end
L=zeros(1,N);%生成Legendre多项式矩阵
L(1,1)=1;
L(1,2)=x;
for i=2:N-1
    L(1,i+1)=((2*i-1)*x*L(1,i)-(i-1)*L(1,i-1))/i;
end
end

Legendre多项式的导数

对于\(x\)​​的一阶导数\(P_{n}'(x)\)​​存在类似的递推公式

\[\begin{align}
(n+1)P'_{n+1}(x)=(2n+1)\{x \cdot P'_{n-1}(x)+P_{n-1}(x)\}-nP'_{n-1}(x) \qquad (n\ge2)
\end{align}
\]

化简得到一阶导数项的递推公式与之前形式类似，但包含额外一项\((2n+1)P_{n-1}(x)\)

\[\begin{align}
(n+1)P'_{n+1}(x)=(2n+1)x \cdot P'_{n-1}(x)-nP'_{n-1}(x) +(2n+1)P_{n-1}(x) \qquad (n\ge2)
\end{align}
\]

Legendre多项式前几项

\(n\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(P'_{n}(x)\)​	\(0\)	\(1\)​	\(3x\)​	\(\frac{1}{2}(15x^2-3)\)​	\(\frac{1}{2}(35x^3-15x)\)​​​​

%% Legendre多项式Pi(x)对于x的一阶导数
function L_x=myLegendre_x(N,x)
L=myLegendre(N,x);
L_x=zeros(1,N);%生成Legendre_x多项式矩阵
L_x(1,1)=0;
L_x(1,2)=1;
for i=2:N-1
    L_x(1,i+1)=((2*i-1)*x*L_x(1,i)-(i-1)*L_x(1,i-1)+(2*i-1)*L(1,i))/i;
end
end

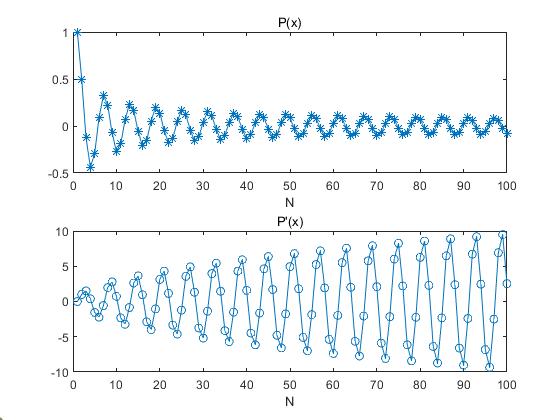
计算结果

%%demo
x=0.5;N=100;
c=myLegendre(N,x);
c_x=myLegendre_x(N,x);
figure(2)
subplot(2,1,1)
plot(c,'-*');xlabel('N');title("P(x)")
subplot(2,1,2)
plot(c_x,'-o');xlabel('N');title("P'(x)")