Robust De-noising by Kernel PCA

目录

• 引
• 主要内容

Takahashi T, Kurita T. Robust De-noising by Kernel PCA[C]. international conference on artificial neural networks, 2002: 739-744.

引

这篇文章是基于对Kernel PCA and De-Noisingin Feature Spaces的一个改进。

针对高斯核：

\[k(x,y) = \exp (-\|x-y\|^2/c)
\]

我们希望最小化下式（以找到\(x\)的一个近似的原像):

\[\rho(z) = \|\Phi(z) - P_H \Phi(x)\|^2
\]

获得了一个迭代公式：

\[z(t) = \frac{\sum_{i=1}^N w_i k(x_i, z(t-1))x_i}{\sum_{i=1}^N w_i k(x_i, z(t-1))}
\]

其中\(w_i=\sum_{h=1}^Hy_h u_i^h\),\(u\)通过求解kernel PCA获得（通常是用\(\alpha\)表示的）,\(z(0)=x\)。

主要内容

虽然我们可以通过撇去小特征值对应的方向，但是这对于去噪并不足够。Kernel PCA and De-Noisingin Feature Spaces中所提到的方法，也就是上面的那个迭代的公式，也没有很好地解决这个问题。既然\(\{y_h\}\)并没有改变——也就是说，我们可能一直在试图用带噪声的数据去恢复一个不带噪声的数据。

所以，作者论文，在迭代更新过程中，\(y_h\)也应该进行更新。

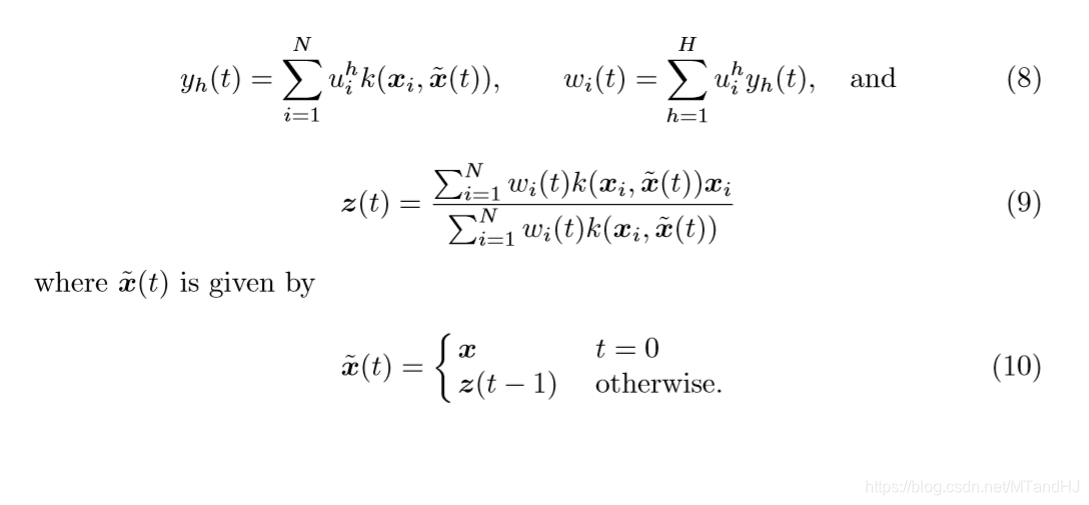
这样，每一步我们都可以看作是在寻找：

\[\|\Phi(z)-P_H\Phi(\widetilde{x}(t)\|
\]

的最小值。

从\((10)\)可以发现，除非\(\widetilde{x}(t)=z(t-1)\)是\(x\)的一个比较好的估计，否则，通过这种方式很有可能会失败（这里的失败定义为，最后的结果与\(x\)差距甚远)。这种情况我估计是很容易发生的。所以，作者提出了一种新的，更新\(\widetilde{x}(t)\)的公式：



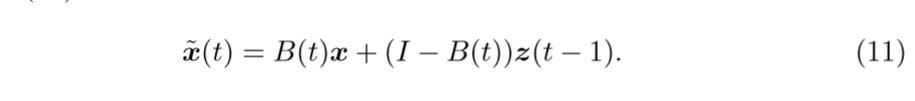
其中\(B(t)\)为确定度，是一个\(M \times M\)的矩阵，定义为：

\[B(t) = diag(\beta_1(t), \ldots, \beta_M(t)) \\
\beta_j(t) = \exp (-(x_j - z_j (t-1))^2/2\sigma_j^2)
\]

对角线元素，反映了\(x_j\)和\(z_j(t-1)\)的差距，如果二者差距不大，说明\(P_H(x)\)和\(x\)的差距不大，\(x\)不是异常值点，所以，结果和\(x\)的差距也不会太大，否则\(x\)会被判定为一个异常值点，自然\(z\)应该和\(x\)的差别大一点。

\(\sigma_j\)的估计是根据另一篇论文来的，这里只给出估计的公式：



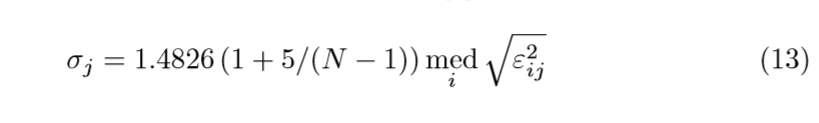
\(\mathrm{med}(x)\)表示\(x\)的中位数，\(\varepsilon_{ij}\)表示第\(i\)个训练样本第\(j\)个分量与其重构之间平方误差。话说，这个重构如何获得呢？