蓝桥杯练习 Day6 题解

蓝桥杯练习 Day6 题解

A

题意：给你一个等式ax+by = c，问你x,y是否有整数解。

思路：gcd(a,b) = t,如果方程有解,那么\((a/t)*x + (b/t)*y = c/t\)

方程\((a/t)*x + (b/t)*y=1\)是肯定有整数解的求得\(x'\),\(y'\),上式右边乘\((a/t)*x' + (b/t)*y'\)可求得\(x = (c/t)*x'\),那么\(x\)要为整数就必须有\(c/t\)为整数，及\(c\)能整除\(t\).

#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
int  gcd(int n,int m)
{
    if(m == 0)
        return n;
    else return gcd(m,n%m);
}
int main(void)
{
    int T,cn = 0;
    scanf("%d",&T);
    while(T--)
    {
        int n,m,c;
        scanf("%d %d %d",&n,&m,&c);
        LL gc = gcd(n,m);
        printf("Case %d: ",++cn);
        if(c%gc == 0)
            printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

B

题意：给\(N\)个球标号为\([1,N]\)；从里面一下子抽取两个球，问这两个球上数字和小于\(k\)的概率；

思路：这题数据比较水暴力也能过。

先分\(k\)为奇偶讨论一下，如果k为偶数，\(cnt = (k-1)/2\);那么小于\(cnt\)的数和另一个数组合小于k的方案数为\(f-1\)(假设那个数为\(f\))，大于\(cnt\)的数和另一个数组合方案数为\((N-f)\)个，所以大于\(cnt\)和小于\(cnt\)两边的符合要求个数是对称的，那么总的符合要求的个数为\(a = (cnt + 1)*cnt\),当\(k\)为奇数时可以同样去推一下.总的方案数为\(b=N*(N-1)/2\),最后求下gcd化简下\((a/b)\).

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL gcd(LL n,LL m);
int main(void)
{
    LL n,m;
    while(scanf("%lld %lld",&n,&m),n!=-1&&m!=-1)
    {
         LL b = n*(n-1)/2;
         LL a = 0;
         if(m%2)
         {
             LL cnt = (m-1)/2;
             a = ((LL)1+cnt)*cnt;
             a -= cnt;
         }
         else
         {   LL cnt = (m-1)/2;
             a = ((LL)1+cnt)*cnt;
         }
         LL gc = gcd(a,b);
         if(a == 0)printf("0\n");
         else if(a == b)printf("1\n");
         else
         printf("%lld/%lld\n",a/gc,b/gc);
    }
    return 0;
}
LL gcd(LL n,LL m)
{
    if(m == 0)return n;
    else return gcd(m,n%m);
}

C

题意：从一个点开始，然后可以向六个方向走，然后问经过\(n\)步后从新回到开始的点的方案数有多少种.

思路:记忆化搜索；

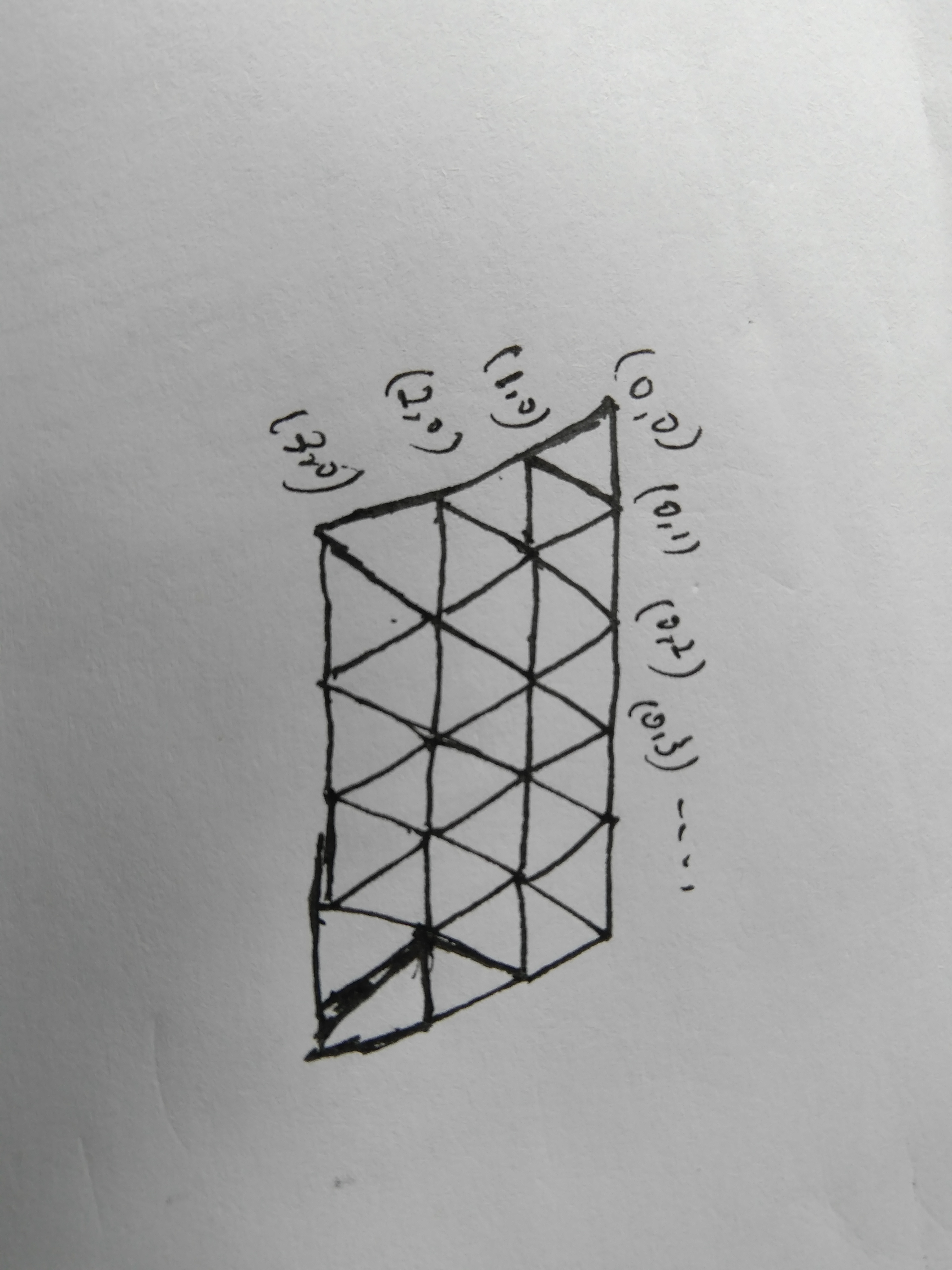
先取个起点(50,50),因为最多走14步，所以不可能超出边界.\(dp[n][m][k]\)表示走k步走到点\((n,m)\)的方案数，那么\(dp[n][m][k] = sum(dp[n+tx][m+ty][k-1])\) \(tx,ty\)表示的是6的不同方向上的对于当前点的增量。那么末状态为\(dp[n][m][k]\),然后记忆化搜索，复杂度为O(\(6*k^3\)).

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL dp[100][100][15];
int xx[6] = {0,-1,-1,0,1,1};//增量数组
int yy[6] = {-1,0,1,1,0,-1};
int slove(int n,int m,int k);
int main(void)
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        memset(dp,0,sizeof(dp));
        int ask = slove(50,50,n);
        ask = max(ask,0);
        printf("%d\n",ask);
    }
    return 0;
}
int slove(int n,int m,int k)
{
    if(dp[n][m][k] == -1)return -1;//当前状态不可到达
    else if(dp[n][m][k])return dp[n][m][k];//当前状态可到达，如果已经被搜到过直接返回方案数
    if(k == 1)//当k为1时只能在起始点的6个方向
    {
        if(n == 50&&m == 49)
            return dp[n][m][k] = 1;
        if(n == 49&&m == 50)
            return dp[n][m][k] = 1;
        if(n == 49&&m == 51)
            return dp[n][m][k] = 1;
        if(n == 50&&m == 51)
            return dp[n][m][k] = 1;
        if(n == 51&&m == 50)
            return dp[n][m][k] = 1;
        if(n == 51&&m == 49)
            return dp[n][m][k] = 1;
        else return dp[n][m][k] = -1;
    }
    int sum = 0;
    for(int i = 0;i <= 5;i++)
    {   int nx = n + xx[i];
        int ny = m + yy[i];
        int ask = slove(nx,ny,k-1);
        if(ask!=-1)
        {
            sum += ask;
        }
    }
    if(sum!=0)return dp[n][m][k] = sum;
    else return dp[n][m][k] = -1;
}

D

题意：将给你的字串按要求输出.

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
char str[205];
char maxtr[20][20];
int main(void)
{
    int n;
    while(scanf("%d",&n),n!=0)
    {
        scanf("%s",str);
        int l = strlen(str);
        int cnt = 0,x = 0,y = 0;
        for(int i = 0; i < l; i++)
        {
            maxtr[x][y] = str[i];
            if(cnt%2)
            {
                y--;
                if(y == -1)
                    y++,x++,cnt++;
            }
            else
            {
                y++;
                if(y == n)
                    y--,x++,cnt++;
            }
        }
        for(int j = 0; j < n; j++)
        {
            for(int i = 0; i < x; i++)
            {
                printf("%c",maxtr[i][j]);
            }
        }
        printf("\n");
    }
    return 0;
}

E

题意：找出第\(k\)个立方的后三位是888的数.

思路：没思路打表找下规律，可以发现要找的数的末三为有4种可能s={\(192,442,692，942\)},那么4个一循环.让最后的解为\(head*1000 + t（t \in s）\),\(head\)开始为0，那么每4个过后\(head\)都加1.

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
void slove(LL n);
int table[4] = {942,192,442,692};
int main(void)
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n;
        scanf("%lld",&n);
        slove(n);
    }
    return 0;
}
void slove(LL n)
{
    LL head = n/4;
    if(n%4==0)head--;
    head*=(LL)1000;
    head += table[n%4];
    printf("%lld\n",head);
}

F

题意：

问\([a,b]\)中的数的约数的个数为\(n\)的个数的个数.

因为\(b-a <= 10^4\),可以想到枚举约数\([1,sqrt(b)]\),然后开个数组记录在\([a,b]\)每个数的约数个数，复杂度O(\(sqrt(b)*log(b-a)\))

#include<bits/stdc++.h>
using namespace std;
int cnt[10005];
int main(void)
{
    int a,b,n;
    scanf("%d %d %d",&a,&b,&n);
    for(int i = 1; i <= sqrt(b); i++)
    {
        for(int j = a/i; j <= b/i + 1; j++)
        {
            if(j*i >= a&&j*i <= b)
            {
                if(j<=sqrt(b))cnt[j*i-a]++;
                else cnt[j*i-a] += 2;
            }
        }
    }
    int sum = 0;
    for(int i = 0; i <= b-a; i++)
    {
        if(cnt[i] == n)
            sum++;
    }
    printf("%d\n",sum);
    return 0;
}

G

思路：根据题意可知没有环，可知任意两点之间若有路径，则经过的边数必不超过1，若超过1就不满足条件了。首先按给出的矩阵建图，然后对每个点bfs或dfs一次，判断是否有超过1的路径

#include <bits/stdc++.h>
using namespace std;

const int N = 2100;
vector<int> vec1[N], vec2[N];
int dis[N];
char str[N];
bool bfs(int s, vector<int> vec[])
{
    queue<int> que;
    memset(dis, 0, sizeof dis);

    que.push(s);
    while(! que.empty())
    {
        int v = que.front(); que.pop();
        for(int i = 0; i < vec[v].size(); i++)
        {
            int u = vec[v][i];
            if(dis[u] == 0)
            {
                if(v != s) return false;
                dis[u] = dis[v] + 1, que.push(u);
                if(dis[u] > 1) return false;
            }
        }
    }
    return true;
}
int main()
{
    int t, n;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%s", str+1);
            for(int j = 1; j <= n; j++)
            {
                if(str[j] == 'P') vec1[i].push_back(j);
                if(str[j] == 'Q') vec2[i].push_back(j);
            }
        }
        bool flag = true;
        for(int i = 1; i <= n; i++)
        {
            if(! bfs(i, vec1))
            {
                flag = false; break;
            }
            if(! bfs(i, vec2))
            {
                flag = false; break;
            }
        }
        if(! flag) printf("N\n");
        else printf("T\n");
        for(int i = 1; i <= n; i++)
            vec1[i].clear(), vec2[i].clear();
    }
    return 0;
}