Manacher算法 求 最长回文子串

1 概述（扯淡）

在了解Manacher算法之前，我们得先知道什么是回文串和子串。

回文串，就是正着看反着看都一样的字符串。比如说“abba”就是一个回文串，“abbc”则不是一个回文串。

一个字符串的子串，就是原字符串中连续的一段字符。比如说“abc”就是“abcdefg”的子串，“ace”和“bsp”则不是“abcdefg”的子串。

那么，一个字符串的最长回文子串就是这个字符串所有为回文串的子串中最长的一个子串。Manacher（马拉车）这个算法要求解的，就是一个字符串中的最长回文子串。

2 算法流程

2.0 准备工作

回文串可以分为两种，一种是长度为奇数的回文串，比如说“cac”；一种是长度为偶数的回文串，比如说“acca”。

这样的话，我们就要分开来处理，好麻烦的咯。其实，我们可以在每两个字符的中间以及开头和结尾插入一个特殊字符，比如说“#”。这样的话，所有的回文串的长度就都变成奇数的了。

举个例子，有一个字符串“aabbabba”，将其进行上述处理后，就变成了这样：“#a#a#b#b#a#b#b#a#”。为了减少边界的处理，我们还可以再在首尾插入两个特殊字符，这两个特殊字符必须和之前插入的特殊字符不相同，并且这两个字符之间也不能相同，比如说“$”和“@”。于是，“#a#a#b#b#a#b#b#a#”就变成了“$#a#a#b#b#a#b#b#a#@”。

值得注意的是，当按照上述方法对字符串进行处理时，不要忘了数组要开到字符串长度的两倍。

（我不会告诉你我Mancher模板因为数组开小RE爆了一次零）

至此，我们的准备工作就做完了。

2.1 正式处理

先给出几个说明：

p：当前已知的所有回文串中，右端点最靠右的回文串的中心。

maxp：当前已知的所有回文串中，右端点最靠右的回文串的右端点

位置i的回文半径：设以位置i为中心的所有回文串中，最长的回文串所对应的区间[l,r]，则位置i的回文半径为区间[i,r]的长度。比如说在字符串“wabbba”中，位置4的回文半径即为3。

r[i]：位置i的回文半径。

我们现在的任务就是对于每一个位置i，都求出其r[i]。这样，我们就可通过r[i]来直接算出最长回文子串的长度了。

假如我们当前已经处理到了字符串的第i个位置，则有以下几种情况：

1.i>maxp

当出现这种情况时，直接暴力扩展求出r[i]。

2.i≤maxp

这时，我们设j为i关于p的对称点，则j=p-(i-p)。

　　2.1.maxp-i+1>r[j]

　　这时，我们直接令r[i]=r[j]即可。因为i和j此时都处于一个回文串内，且分别在这个回文串的中心p的两侧，r[i]也并没有延伸到这个回文串的边界或边界以外，所以两边的情况是相同的，直接赋值即可。

　　图示：

　　

　　2.2.maxp-i+1≤r[j]

　　这时，我们先令r[i]=maxp-i+1，然后再暴力扩展更新r[i]即可。为什么这时不能直接将r[j]的值赋给r[i]呢？这是因为，r[j]已经延伸到了以p为中心的回文串的边界或边界之外，回文串两侧外的情况是不同的，所以不能像上一种情况那样直接赋值。

　　图示：

　　

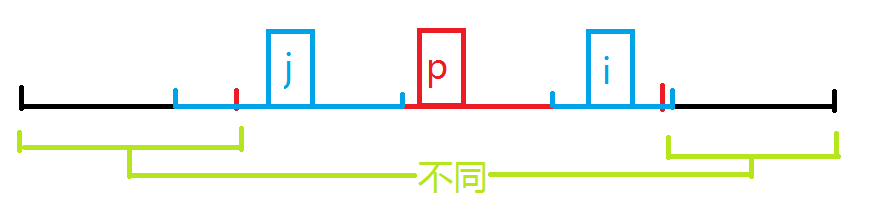
最后，我们维护一下p，maxp和答案就好。

3 时间复杂度

不难看出，Mancher算法的时间复杂度为O(n)，其中n为字符串的长度。这是因为每个r[i]暴力扩展次数的总和是不会超过n次的（想想为什么）。

4 代码实现

#include<iostream>
#include<cstdio>
#include<cstring>
    using namespace std;
    int r[22000005];
    char st[22000005];
int main()
{
    int k=0;
    char ch=' ';
    while(ch<'a'||ch>'z') ch=getchar();                          //---|
    st[0]='$',st[++k]='#';                                       //   |-读入字符串
    while(ch>='a'&&ch<='z') st[++k]=ch,st[++k]='#',ch=getchar(); //   |-并插入特殊字符
    st[k+1]='@';                                                 //---|
    int p=0,ans=0,maxp=0;
    for(int i=1;i<=k;i++)
    {
        if(i>maxp)                                           //------|
            while(st[i-r[i]]==st[i+r[i]]) r[i]++;            //      |
        else                                                 //      |-分
        {                                                    //      |-情
            int j=p-(i-p);                                   //      |-况
            if(maxp-i+1>r[j]) r[i]=r[j];                     //      |-处
            if(maxp-i+1<=r[j])                               //      |-理
            {                                                //      |
                r[i]=maxp-i+1;                               //      |
                while(st[i-r[i]]==st[i+r[i]]) r[i]++;        //      |
            }                                                //      |
        }                                                    //------|
        if(i+r[i]-1>maxp) maxp=i+r[i]-1,p=i;//维护maxp和p
        ans=max(ans,(r[i]+r[i]-1)>>1);//更新答案
    }
    printf("%d",ans);
    return 0;
} 

5 练习题

Luogu P3805 【模板】manacher算法

Luogu P1659 [国家集训队]拉拉队排练

Luogu P4555 [国家集训队]最长双回文串