在C＃中使用RSA进行加密和解密

这篇文章向您展示了如何在c＃.net Windows窗体应用程序中使用RSA算法对字符串进行加密和解密。
RSA是由Ron Rivest，Adi Shamir和Leonard Adleman开发的非对称编码系统（其名称也是这三位作者的缩写）。它被广泛用于加密和电子签名技术。它通过使用公共密钥与所有人共享来工作。

RSA操作基于四个主要步骤：密钥生成，密钥共享，加密和解密。

本文将介绍有关c＃rsa生成公共和私有密钥的算法，密钥如何在c＃中进行加密和解密。

拖动 文本框，标签和按钮从Visual Studio工具箱到您的WinForm设计，那么你可以设计一个简单的用户界面，使您可以加密和使用C＃代码RSA算法解密字符串，如下图所示。

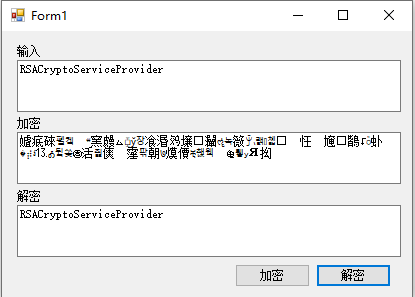
在C＃中使用RSA算法进行加密和解密
通过本c＃密码学教程，我将创建一个Encrypt方法来使用RSA算法加密您的数据。

byte[] Encrypt(byte[] data, RSAParameters RSAKey, bool fOAEP)
{
    byte[] encryptedData;
    using (RSACryptoServiceProvider rSACryptoServiceProvider = new RSACryptoServiceProvider())
    {
        rSACryptoServiceProvider.ImportParameters(RSAKey);
        encryptedData = rSACryptoServiceProvider.Encrypt(data, fOAEP);
    }
    return encryptedData;
}

同样，创建  Decrypt方法以使用RSA算法解密数据。

byte[] Decrypt(byte[] data, RSAParameters RSAKey, bool fOAEP)
{
    byte[] decryptedData;
    using (RSACryptoServiceProvider rSACryptoServiceProvider = new RSACryptoServiceProvider())
    {
        rSACryptoServiceProvider.ImportParameters(RSAKey);
        decryptedData = rSACryptoServiceProvider.Decrypt(data, fOAEP);
    }
    return decryptedData;
}

C＃RSA用公钥加密
接下来，声明 unicodeEncoding， rSACryptoServiceProvider， data 和 cryptoData变量，如下所示。

UnicodeEncoding unicodeEncoding = new UnicodeEncoding();
RSACryptoServiceProvider rSACryptoServiceProvider = new RSACryptoServiceProvider();
byte[] data;
byte[] encryptData;

最后，使用RSA通过调用ExportParameters方法来生成公钥和私钥  。

rSACryptoServiceProvider.ExportParameters(false)

RSA算法使用密钥在c＃中执行加密和解密。

将单击事件处理程序添加到“  加密”按钮后，即可使用RSA算法对数据进行加密。

private void btnEncrypt_Click(object sender, EventArgs e)
{
    data = unicodeEncoding.GetBytes(txtInput.Text);
    encryptData = Encrypt(data, rSACryptoServiceProvider.ExportParameters(false), false);
    txtEncrypt.Text = unicodeEncoding.GetString(encryptData);
}

将单击事件处理程序添加到“ 解密” 按钮，使您可以解密数据。

private void btnDecrypt_Click(object sender, EventArgs e)
{
    byte[] data = Decrypt(encryptData, rSACryptoServiceProvider.ExportParameters(true), false);
    txtDecrypt.Text = unicodeEncoding.GetString(data);
}