Pyramid of Glasses（递推）

Pyramid of Glasses

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mary has just graduated from one well-known University and is now attending celebration party. Students like to dream of a beautiful life, so they used champagne glasses to construct a small pyramid. The height of the pyramid is n. The top level consists of only 1 glass, that stands on 2glasses on the second level (counting from the top), then 3 glasses on the third level and so on.The bottom level consists of n glasses.

Vlad has seen in the movies many times how the champagne beautifully flows from top levels to bottom ones, filling all the glasses simultaneously. So he took a bottle and started to pour it in the glass located at the top of the pyramid.

Each second, Vlad pours to the top glass the amount of champagne equal to the size of exactly one glass. If the glass is already full, but there is some champagne flowing in it, then it pours over the edge of the glass and is equally distributed over two glasses standing under. If the overflowed glass is at the bottom level, then the champagne pours on the table. For the purpose of this problem we consider that champagne is distributed among pyramid glasses immediately. Vlad is interested in the number of completely full glasses if he stops pouring champagne in t seconds.

Pictures below illustrate the pyramid consisting of three levels.

Input

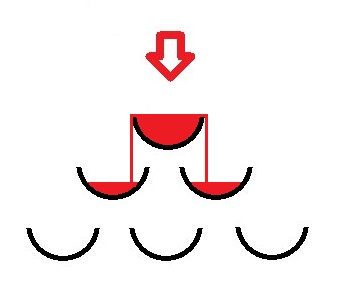
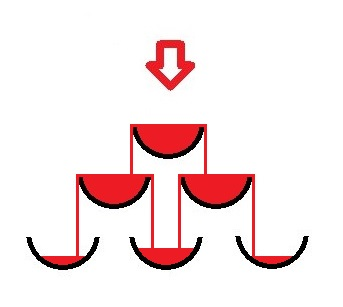
The only line of the input contains two integers n and t (1 ≤ n ≤ 10, 0 ≤ t ≤ 10 000) — the height of the pyramid and the number of seconds Vlad will be pouring champagne from the bottle.

Output

Print the single integer — the number of completely full glasses after t seconds.

Examples

input

3 5

output

4

input

4 8

output

6

Note

In the first sample, the glasses full after 5 seconds are: the top glass, both glasses on the second level and the middle glass at the bottom level. Left and right glasses of the bottom level will be half-empty.

题意：每1s会从上面多出一杯子的水，然后问你t秒后会有多少个杯子是满的，n代表有多少层杯子

题解：找到递推式的话，这题并不难。我们考虑，每个杯子（除了最上面那个），他们获得的水都是从上面两边获得，而上面的杯子的水只会流向两边，那么递推式就很明显了。我们假设杯子容量为1，那状态就是dp[i][j]=(dp[i-1][j-1]-1)/2+(dp[i-1][j]-1)/2;初始条件dp[1][1]=t*1;一路推下来，记录dp[i][j]>=1的个数，即为答案。

#include <cstdio>
using namespace std;
double dp[][];
int main()
{
    int n,t,ans=;
    scanf("%d%d",&n,&t);
    dp[][]=t;
    for (int i=;i<=n;i++)
    for (int j=;j<=i;j++)
    {
        if (dp[i-][j-]>)
        dp[i][j]+=(dp[i-][j-]-)/;
        if (dp[i-][j]>)
        dp[i][j]+=(dp[i-][j]-)/;
        if (dp[i][j]>=) ans++;
    }
    printf("%d\n",t==?:ans);
}