FpGrowth算法

FpGrowth算法

频繁项集与关联规则挖掘(2)--FpGrowth算法

 

　　上一篇介绍了关联规则挖掘的一些基本概念和经典的Apriori算法，Aprori算法利用频繁集的两个特性，过滤了很多无关的集合，效率提高不少，但是我们发现Apriori算法是一个候选消除算法，每一次消除都需要扫描一次所有数据记录，造成整个算法在面临大数据集时显得无能为力。今天我们介绍一个新的算法挖掘频繁项集，效率比Aprori算法高很多。

　　FpGrowth算法通过构造一个树结构来压缩数据记录，使得挖掘频繁项集只需要扫描两次数据记录，而且该算法不需要生成候选集合，所以效率会比较高。我们还是以上一篇中用的数据集为例：

TID	Items
T1	{牛奶,面包}
T2	{面包,尿布,啤酒,鸡蛋}
T3	{牛奶,尿布,啤酒,可乐}
T4	{面包,牛奶,尿布,啤酒}
T5	{面包,牛奶,尿布,可乐}

一、构造FpTree

　　FpTree是一种树结构，树结构定义如下：

public class FpNode {

    String idName;// id号
    List<FpNode> children;// 孩子结点
    FpNode parent;// 父结点
    FpNode next;// 下一个id号相同的结点
    long count;// 出现次数
} 

　　树的每一个结点代表一个项，这里我们先不着急看树的结构，我们演示一下FpTree的构造过程，FpTree构造好后自然明白了树的结构。假设我们的最小绝对支持度是3。

　　Step 1：扫描数据记录，生成一级频繁项集，并按出现次数由多到少排序，如下所示：

Item	Count
牛奶	4
面包	4
尿布	4
啤酒	3

　　可以看到，鸡蛋和可乐没有出现在上表中，因为可乐只出现2次，鸡蛋只出现1次，小于最小支持度，因此不是频繁项集，根据Apriori定理，非频繁项集的超集一定不是频繁项集，所以可乐和鸡蛋不需要再考虑。

　　Step 2：再次扫描数据记录，对每条记录中出现在Step 1产生的表中的项，按表中的顺序排序。初始时，新建一个根结点，标记为null；

　　1）第一条记录：{牛奶,面包}，按Step 1表过滤排序得到依然为{牛奶,面包}，新建一个结点，idName为{牛奶}，将其插入到根节点下，并设置count为1，然后新建一个{面包}结点，插入到{牛奶}结点下面，插入后如下所示：

　　2）第二条记录：{面包,尿布,啤酒,鸡蛋}，过滤并排序后为：{面包,尿布,啤酒}，发现根结点没有包含{面包}的儿子（有一个{面包}孙子但不是儿子），因此新建一个{面包}结点，插在根结点下面，这样根结点就有了两个孩子，随后新建{尿布}结点插在{面包}结点下面，新建{啤酒}结点插在{尿布}下面，插入后如下所示：

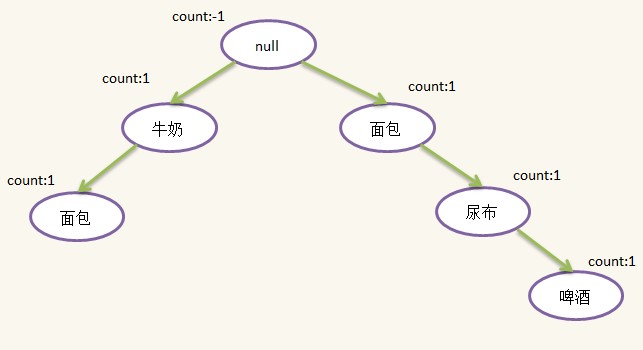
　　3）第三条记录：{牛奶,尿布,啤酒,可乐}，过滤并排序后为：{牛奶,尿布,啤酒}，这时候发现根结点有儿子{牛奶}，因此不需要新建结点，只需将原来的{牛奶}结点的count加1即可，往下发现{牛奶}结点有一个儿子{尿布}，于是新建{尿布}结点，并插入到{牛奶}结点下面，随后新建{啤酒}结点插入到{尿布}结点后面。插入后如下图所示：

　　4）第四条记录：{面包,牛奶,尿布,啤酒}，过滤并排序后为：{牛奶，面包,尿布,啤酒}，这时候发现根结点有儿子{牛奶}，因此不需要新建结点，只需将原来的{牛奶}结点的count加1即可，往下发现{牛奶}结点有一个儿子{面包}，于是也不需要新建{面包}结点，只需将原来{面包}结点的count加1，由于这个{面包}结点没有儿子，此时需新建{尿布}结点，插在{面包}结点下面，随后新建{啤酒}结点，插在{尿布}结点下面，插入后如下图所示：

　　

　　5）第五条记录：{面包,牛奶,尿布,可乐}，过滤并排序后为：{牛奶，面包,尿布}，检查发现根结点有{牛奶}儿子，{牛奶}结点有{面包}儿子，{面包}结点有{尿布}儿子，本次插入不需要新建结点只需更新count即可，示意图如下：

　　

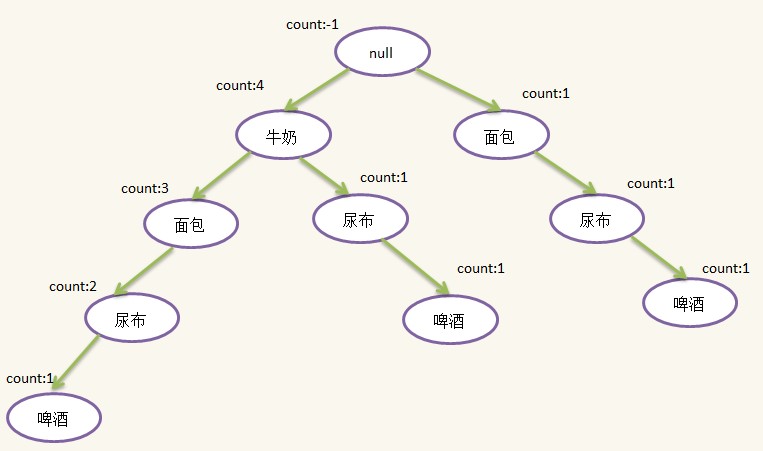
　　按照上面的步骤，我们已经基本构造了一棵FpTree（Frequent Pattern Tree），树中每天路径代表一个项集，因为许多项集有公共项，而且出现次数越多的项越可能是公公项，因此按出现次数由多到少的顺序可以节省空间，实现压缩存储，另外我们需要一个表头和对每一个idName相同的结点做一个线索，方便后面使用，线索的构造也是在建树过程形成的，但为了简化FpTree的生成过程，我没有在上面提到，这个在代码有体现的，添加线索和表头的Fptree如下：

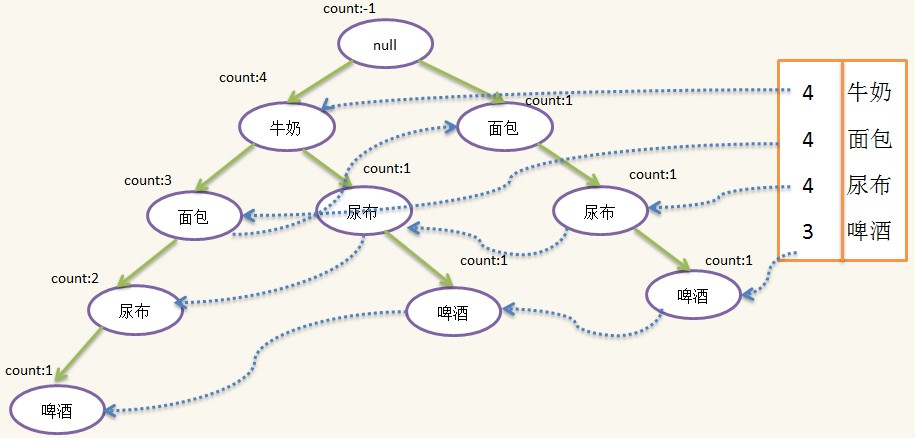
　　至此，整个FpTree就构造好了，在下面的挖掘过程中我们会看到表头和线索的作用。

二、利用FpTree挖掘频繁项集

　　FpTree建好后，就可以进行频繁项集的挖掘，挖掘算法称为FpGrowth（Frequent Pattern Growth）算法，挖掘从表头header的最后一个项开始。

　　1）此处即从{啤酒}开始，根据{啤酒}的线索链找到所有{啤酒}结点，然后找出每个{啤酒}结点的分支：{牛奶，面包，尿布，啤酒：1}，{牛奶，尿布，啤酒:1}，{面包，尿布，啤酒:1}，其中的“1”表示出现1次，注意，虽然{牛奶}出现4次，但{牛奶，面包，尿布，啤酒}只同时出现1次，因此分支的count是由后缀结点{啤酒}的count决定的，除去{啤酒}，我们得到对应的前缀路径{牛奶，面包，尿布：1}，{牛奶，尿布:1}，{面包，尿布:1}，根据前缀路径我们可以生成一颗条件FpTree，构造方式跟之前一样，此处的数据记录变为：

TID	Items
T1	{牛奶，面包，尿布}
T2	{牛奶，尿布}
T3	{面包，尿布}

　　绝对支持度依然是3，构造得到的FpTree为：

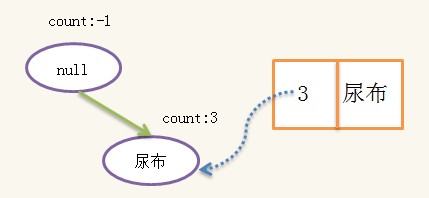
构造好条件树后，对条件树进行递归挖掘，当条件树只有一条路径时，路径的所有组合即为条件频繁集，假设{啤酒}的条件频繁集为{S1,S2,S3}，则{啤酒}的频繁集为{S1+{啤酒},S2+{啤酒},S3+{啤酒}}，即{啤酒}的频繁集一定有相同的后缀{啤酒}，此处的条件频繁集为：{{}，{尿布}}，于是{啤酒}的频繁集为{{啤酒}{尿布，啤酒}}。

　　2）接下来找header表头的倒数第二个项{尿布}的频繁集，同上可以得到{尿布}的前缀路径为：{面包：1}，{牛奶：1}，{牛奶，面包：2}，条件FpTree的数据集为：

TID	Items
T1	{面包}
T2	{牛奶}
T3	{牛奶，面包}
T4	{牛奶，面包}

　　注意{牛奶，面包：2}，即{牛奶，面包}的count为2，所以在{牛奶，面包}重复了两次，这样做的目的是可以利用之前构造FpTree的算法来构造条件Fptree，不过这样效率会降低，试想如果{牛奶，面包}的count为20000，那么就需要展开成20000条记录，然后进行20000次count更新，而事实上只需要对count更新一次到20000即可。这是实现上的优化细节，实践中当注意。构造的条件FpTree为：

 　　这颗条件树已经是单一路径，路径上的所有组合即为条件频繁集：{{}，{牛奶}，{面包}，{牛奶，面包}}，加上{尿布}后，又得到一组频繁项集{{尿布}，{牛奶，尿布}，{面包，尿布}，{牛奶，面包，尿布}}，这组频繁项集一定包含一个相同的后缀：{尿布}，并且不包含{啤酒}，因此这一组频繁项集与上一组不会重复。

　　重复以上步骤，对header表头的每个项进行挖掘，即可得到整个频繁项集，可以证明（严谨的算法和证明可见参考文献[1]），频繁项集即不重复也不遗漏。

　程序的实现代码还是放在我的github上，这里看一下运行结果：

绝对支持度： 3
频繁项集：
面包 尿布     3
尿布 牛奶     3
牛奶     4
面包 牛奶     3
尿布 啤酒     3
面包     4

　　另外我下载了一个购物篮的数据集，数据量较大，测试了一下FpGrowth的效率还是不错的。FpGrowth算法的平均效率远高于Apriori算法，但是它并不能保证高效率，它的效率依赖于数据集，当数据集中的频繁项集的没有公共项时，所有的项集都挂在根结点上，不能实现压缩存储，而且Fptree还需要其他的开销，需要存储空间更大，使用FpGrowth算法前，对数据分析一下，看是否适合用FpGrowth算法。

　　下一篇将介绍，关联规则的评价标准，欢迎持续关注。

 参考文献：

　　[1].Han jia wei, Pei Jan等 Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach.2004

感谢关注，欢迎回帖交流!

转载请注明出处：http://www.cnblogs.com/fengfenggirl

 

 

 

标签: 数据挖掘