Accord.Net中决策树

Accord.Net中决策树

决策树介绍

决策树是一类机器学习算法，可以实现对数据集的分类、预测等。具体请阅读我另一篇博客（http://www.cnblogs.com/twocold/p/5424517.html）。

Accord.Net

Accord.Net(http://accord-framework.net/)是一个开源的.Net环境下实现的机器学习算法库。并且还包括了计算机视觉、图像处理、数据分析等等许多算法，并且基本上都是用C#编写的，对于.Net程序员十分友好。代码在Github托管，并且现在仍在维护中。（https://github.com/accord-net/framework）。此处不再具体介绍，有兴趣的可以去官网或者Github下载文档和代码深入了解。此处只简单介绍决策树部分的实现和使用方法。

决策树结构

决策树、顾名思义，肯定是一个和树结构，作为最基础的数据结构之一，我们深知树结构的灵活性。那么Accord.Net是如何实现这种结构的呢？看类图

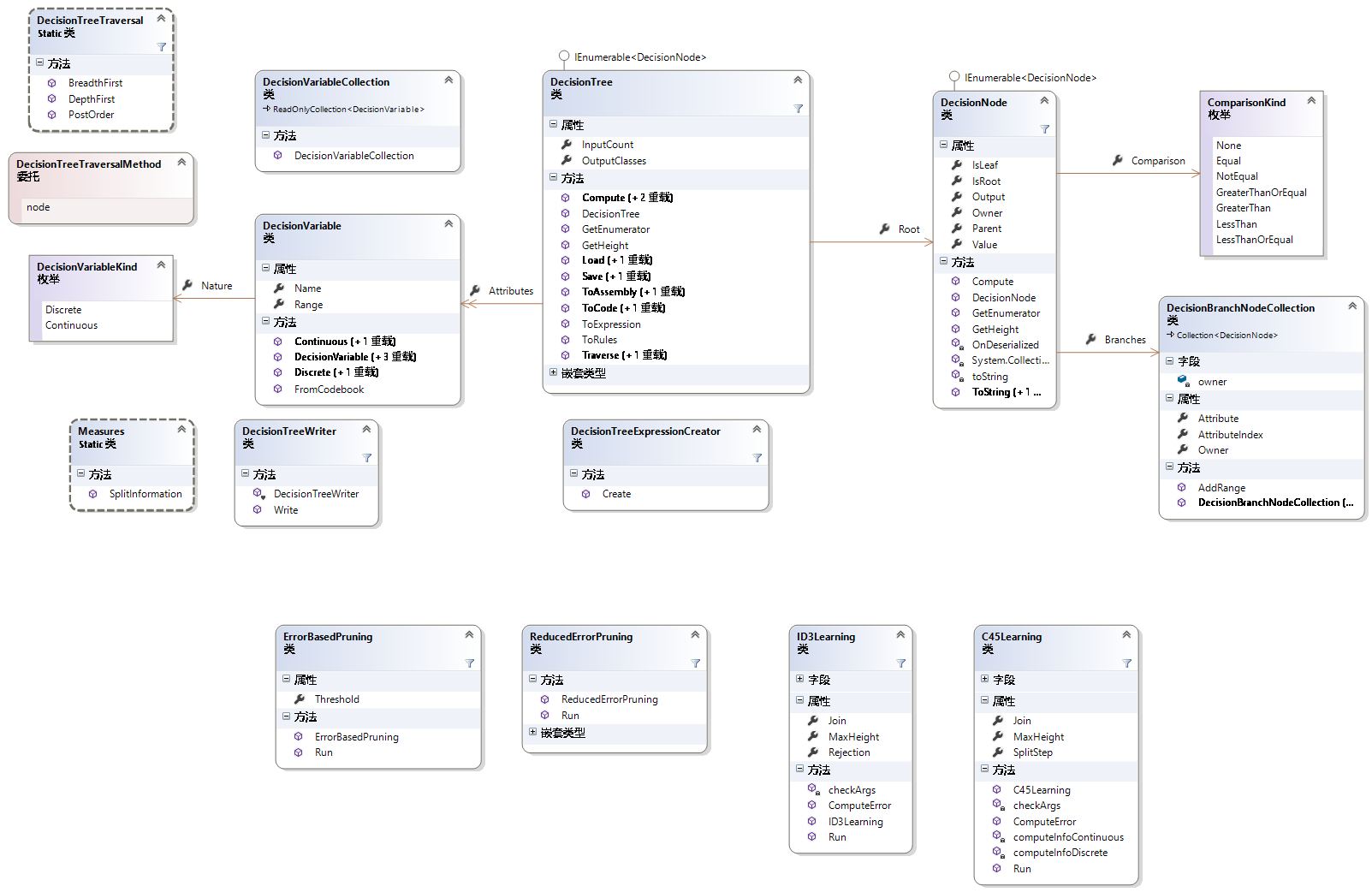
首先观察树结构中最重要的一个结构，Node类的类图如下：

简单介绍下主要属性方法。

属性	含义
IsLeaf	是否为叶子节点
IsRoot	是否为根节点
Output	指示结点的类别信息（叶子节点可用）
Value	为非根节点时，表示其父节点分割特征的值
Branches	为非叶子节点时，表示其子结点的集合

还有树结构：

属性、方法	含义
Root	根节点
Attributes	标识各个特征的信息（连续、离散、范围）
InputCount	特征个数
OutputClasses	输出类别种数
Compute()	计算出某一样本的类别信息
Load(),Save()	将决策树存储到文件或者读出
ToAssembly()	存储到dll程序集中

还有其他依赖项就不再逐一介绍了，Accord的官方文档里都有更加清晰的讲解。

主要想要说的是ID3Learning和C45Learning两个类。这是Accord.Net实现的两个决策树学习（训练）算法，ID3算法和C4.5算法（ID为Iterative Dichotomiser的缩写，迭代二分器；C是Classifier的缩写，即第4.5代分类器）。后面会介绍两者的区别。

决策树学习算法：

这里以一个经典的打网球的例子，介绍ID3算法的学习过程。要理解下面的代码可能需要对决策树的学习过程有个基本的了解，可以参考开头给出的链接学习下决策树的基本概念。

Mitchell's Tennis Example
Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

首先，为了后面进一步构造决策树，我们需要把上面的数据简化一下，以字符串存储和进行比较会消耗大量的内存空间，并且降低效率。考虑到所有特征都为离散特征，可以直接用最简单的整型表示就行，只要保存下数字和字符串的对应关系就行。Accord.Net用了CodeBook来实现，这里也就不具体介绍了。然后需要对树的一些属性进行初始化，比如特征的个数（InputCount），类别数（OutputClasses）。还有每个特征可能的取值个数。接下来就可以利用上面codebook转义过的样本数据进行构造了。

下面贴出ID3算法中递归方法的伪代码，大致讲解下其实现逻辑（注：此代码删去了很多细节，因此无法运行，只大概了解其实现逻辑。）。

        /// <summary>
        /// 决策树学习的分割构造递归方法
        /// </summary>
        /// <param name="root">当前递归结点</param>
        /// <param name="input">输入样本特征</param>
        /// <param name="output">样本对应类别</param>
        /// <param name="height">当前结点层数</param>
        private void split(DecisionNode root, int[][] input, int[] output, int height)
        {
            //递归return条件

            //1.如果output[]都相等，就是说当前所有样本类别相同，则递归结束。结点标记为叶子节点，output值标识为样本类别值           

            double entropy = Statistics.Tools.Entropy(output, outputClasses);

            if (entropy == 0)
            {
                if (output.Length > 0)
                    root.Output = output[0];
                return;
            }

            //2.如果当前路径上所有特征都用过一次了，也就是说现在所有样本在所有特征上取值相同，也就没法划分了；递归结束。结点标记为叶子节点，output值标识为样本类别值最多的那个

            //这个变量存储的是还未使用的特征个数
            int candidateCount = attributeUsageCount.Count(x => x < 1);

            if (candidateCount == 0)
            {
                root.Output = Statistics.Tools.Mode(output);
                return;
            }

            // 如果需要继续分裂，则首先寻找最优分裂特征，
            // 存储剩余所有可以特征的信息增益大小
            double[] scores = new double[candidateCount];
            // 循环计算每个特征分裂时的信息增益存储到scores里

            Parallel.For(0, scores.Length, i =>

            {
                scores[i] = computeGainRatio(input, output, candidates[i],
                    entropy, out partitions[i], out outputSubs[i]);
            }

            // 获取到最大信息增益对应的特征
            int maxGainIndex = scores.Max();
            // 接下来 需要按照特征的值分割当前的dataset，然后传递给子节点 递归
            DecisionNode[] children = new DecisionNode[maxGainPartition.Length];

            for (int i = 0; i < children.Length; i++)
            {
                int[][] inputSubset = input.Submatrix(maxGainPartition[i]);

                split(children[i], inputSubset, outputSubset, height + 1); // 递归每个子节点

            }

            root.Branches.AddRange(children);

        }

此代码仅为方便理解，具体实现细节请自行下载Accord源代码阅读，相信您会有不少收获。

C4.5的实现与ID3算法流程基本相同，有几个不同之处

1) 在选择最优分割特征时，ID3算法采用的是信息增益，C4.5采用的是增益率。

2) C4.5支持连续型特征，因此，在递归进行之前，要采用二分法计算出n-1个候选划分点，将这些划分点当做离散变量处理就和ID3过程一致了。同样是因为连续型变量，这样一条路径下连续型特征可以多次用来分割，而离散型特征每个只能用一次。

3) C4.5支持缺失值的处理，遗憾的是Accord中并没有加入这一特性。

Accord.Net中还给出了简单的剪枝算法，有兴趣可以自行阅读。

以上面的打网球例子，这里给出Accord.Net中构造和训练决策树的代码示例。

           //数据输入 存储为DataTable
             DataTable data = new DataTable("Mitchell's Tennis Example");
            data.Columns.Add("Day");
            data.Columns.Add("Outlook");
            data.Columns.Add("Temperature");
            data.Columns.Add("Humidity");
            data.Columns.Add("Wind");
            data.Columns.Add("PlayTennis");

            data.Rows.Add("D1", "Sunny", "Hot", "High", "Weak", "No");
            data.Rows.Add("D2", "Sunny", "Hot", "High", "Strong", "No");
            data.Rows.Add("D3", "Overcast", "Hot", "High", "Weak", "Yes");
            data.Rows.Add("D4", "Rain", "Mild", "High", "Weak", "Yes");
            data.Rows.Add("D5", "Rain", "Cool", "Normal", "Weak", "Yes");
            data.Rows.Add("D6", "Rain", "Cool", "Normal", "Strong", "No");
            data.Rows.Add("D7", "Overcast", "Cool", "Normal", "Strong", "Yes");
            data.Rows.Add("D8", "Sunny", "Mild", "High", "Weak", "No");
            data.Rows.Add("D9", "Sunny", "Cool", "Normal", "Weak", "Yes");
            data.Rows.Add("D10", "Rain", "Mild", "Normal", "Weak", "Yes");
            data.Rows.Add("D11", "Sunny", "Mild", "Normal", "Strong", "Yes");
            data.Rows.Add("D12", "Overcast", "Mild", "High", "Strong", "Yes");
            data.Rows.Add("D13", "Overcast", "Hot", "Normal", "Weak", "Yes");
            data.Rows.Add("D14", "Rain", "Mild", "High", "Strong", "No");
            // 创建一个CodeBook对象，用于将data中的字符串“翻译”成整型
            Codification codebook = new Codification(data,
              "Outlook", "Temperature", "Humidity", "Wind", "PlayTennis");
            // 将data中的样本特征数据部分和类别信息分别转换成数组
            DataTable symbols = codebook.Apply(data);
            int[][] inputs = Matrix.ToArray<double>(symbols, "Outlook", "Temperature", "Humidity", "Wind");
            int[] outputs = Matrix.ToArray<int>(symbols, "PlayTennis");
            //分析得出每个特征的信息，如，每个特征的可取值个数。
           DecisionVariable[] attributes = DecisionVariable.FromCodebook(codebook, "Outlook", "Temperature", "Humidity", "Wind");

           int classCount = 2; //两种可能的输出，打网球和不打

            //根据参数初始化一个树结构
            DecisionTree tree = new DecisionTree(attributes, classCount);

            // 创建一个ID3训练方法
            ID3Learning id3learning = new ID3Learning(tree);

            // 训练该决策树
            id3learning.Run(inputs, outputs);

            //现在即可使用训练完成的决策树预测一个样本，并借助codebook“翻译”回来
            string answer = codebook.Translate("PlayTennis",tree.Compute(codebook.Translate("Sunny", "Hot", "High", "Strong")));

贴一张利用决策树做的小例子。

 

 

标签: 机器学习, .Net