UVA - 12661 Funny Car Racing （Dijkstra算法）

题目：

思路：

把时间当做距离利用Dijkstra算法来做这个题。

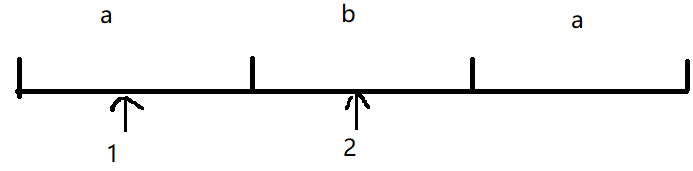
前提：该结点e.c<=e.a,k = d[v]%(e.a+e.b);

当车在这个点的1处时，如果在第一个a这段时间内能够通过且更小的话，那时间就更新为d[e.to] = d[v]+e.a-k+e.c;

当车在这个点的1处时，如果在第一个a这段时间内不能通过，但等待之后再通过时间更短的话，那时间更新为d[e.to]=d[v]+e.a+e.b-k+e.c

如果在这个点的2处时，如果在等待之后通过的时间更短的话，时间更新和第二种情况一样为d[e.to]=d[v]+e.a+e.b-k+e.c

所有的边是有向边，然后用迪杰斯特拉算法解题就可以了。

代码：

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define MAX 1000000000
#define mod 1000000007
#define FRE() freopen("in.txt","r",stdin)
#define FRO() freopen("out.txt","w",stdout)
using namespace std;
typedef long long ll;
typedef pair<int,int> P;//first-距离 second-编号
const int maxn = ;
int d[maxn];
int n,m,s,t;
struct Edge {
    int to,a,b,c;
};
vector<Edge> G[maxn*];

void init() {
    for(int i=; i<maxn*; i++) {
        G[i].clear();
        if(i<maxn) {
            d[i] = inf;
        }
    }
    for(int i=; i<m; i++) {
        int u,v,a,b,c;
        scanf("%d%d%d%d%d",&u,&v,&a,&b,&c);
        G[u].push_back(Edge{v,a,b,c});
    }
}

void Dijstra(){
    priority_queue<P,vector<P>,greater<P> > que;
    d[s] = ;
    que.push(P(,s));
    while(!que.empty()){
        P p = que.top();que.pop();
        int v = p.second;
       // cout<<"GG  "<<v<<endl;
        if(d[v]>p.first) continue;
        //cout<<"size: "<<G[v].size()<<endl;
        for(int i=; i<G[v].size(); i++){
            Edge e = G[v][i];
            int k = d[v]%(e.a+e.b);
            if(k+e.c<=e.a && d[e.to]>d[v]+e.c && e.c<=e.a){
                d[e.to] = d[v]+e.c;
                que.push(P(d[e.to],e.to));
                //cout<<"Fuck!"<<endl;
            }else if(k+e.c>e.a && d[e.to]>d[v]+e.a+e.b-k+e.c && e.c<=e.a){
                d[e.to] = d[v]+e.a+e.b-k+e.c;
                que.push(P(d[e.to],e.to));
                //cout<<"Fuck!"<<endl;
            }
        }
    }
}

int main() {
   // FRE();
    int kase=;
    while(scanf("%d%d%d%d",&n,&m,&s,&t)!=EOF) {
        init();
        Dijstra();
        printf("Case %d: %d\n",++kase,d[t]);
    }
    return ;
}