【解题报告】洛谷 P2571 [SCOI2010]传送带

【解题报告】洛谷 P2571 [SCOI2010]传送带
今天无聊，很久没有做过题目了，但是又不想做什么太难的题目，所以就用洛谷随机跳题，跳到了一道题目，感觉好像不是太难。

[CSDN链接](https://blog.csdn.net/Liang_Si_FFF/article/details/84570359)
[题目链接](https://www.luogu.org/problemnew/show/P2571)

===================================================================================
题目描述

在一个2维平面上有两条传送带，每一条传送带可以看成是一条线段。两条传送带分别为线段AB和线段CD。lxhgww在AB上的移动速度为P，在CD上的移动速度为Q，在平面上的移动速度R。现在lxhgww想从A点走到D点，他想知道最少需要走多长时间

输入输出格式

输入格式：
输入数据第一行是4个整数，表示A和B的坐标，分别为Ax，Ay，Bx，By

第二行是4个整数，表示C和D的坐标，分别为Cx，Cy，Dx，Dy

第三行是3个整数，分别是P，Q，R

输出格式：
输出数据为一行，表示lxhgww从A点走到D点的最短时间，保留到小数点后2位

输入输出样例

输入样例#1：
0 0 0 100
100 0 100 100
2 2 1
 输出样例#1：
136.60
说明

对于100%的数据，1<= Ax，Ay，Bx，By，Cx，Cy，Dx，Dy<=1000

1<=P，Q，R<=10

======================================================================================================

下面是我的分析过程

分析过程

首先，如图

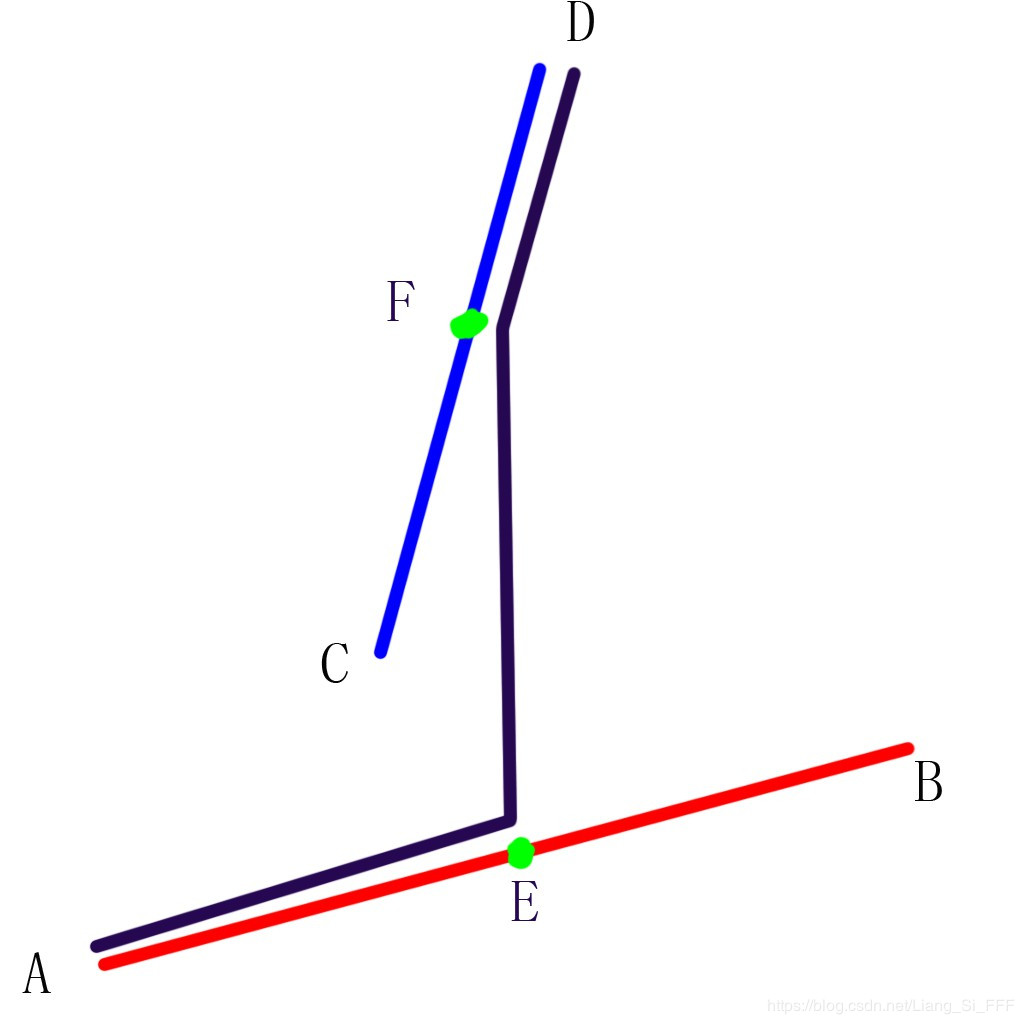
　　1. 通过观察题目，我们可以发现，我们行走的路径一定是先在AB边上走，然后走下AB边，走向CD边，然后在CD边上走。（当然，有可能直接在A点就走下了AB边，也有可能直接从D点上了CD边，这里我们同样看作是先走下AB边，然后走上AB边）所以如果我们在AB边取一个点E,在CD边取一个点F,那么，不同的路径就可以用不同的E点和F点唯一表示，即每一个数对(E,F)都唯一对应一条路径（PS:E点可以和A或B重合，F点可以和C或者D重合）所以，我们可以想到一个朴素的算法：枚举E点和F点。但是这种算法明显是太暴力了，不可能通过的。
　　2. 我们通过仔细思考，可以这么想：假如我现在的E点是已经确定好是哪个点的了，那么我们的问题就可以转换为：已知一条传送带，以及你在传送带上面的速度和地面上的速度，并且知道起点的准确位置，求到达终点的最短时间。
假如题目变成了这个样子，那么我们会发现，随着F点从C点到D点移动，这个总的时间应该是先递减后递增的。由于是一个单峰函数，所以我们可以用三分来做。
　　3. 那么，我们现在的问题就是，这个E点也是移动的。但是我们现在能够做到对于AB边上的每一个点E,都能算出E点固定时的最短时间。所以，相比刚刚开始的同时枚举两个点E和F，现在只需要枚举一下E点就可以了。即：枚举E点的位置，然后对于每一个E点，对F点进行三分，找出每一个E点对应的最小路径的F点是哪一个。
　　4. 但是，这个算法好像还是不太好，因为E点的枚举还是很麻烦的，复杂度一样很高。我们可以大胆猜想，或许E点的取值范围也是可以用三分法来做的！但是我还没有想到证明方法，也只是胡乱瞎猜。不过我猜对了。我还没有找到证明，找到证明之后我会再贴链接或者干啥的。
　　5. 所以，我们现在可以得出一个能够在规定时间得出答案的算法：先三分E点的位置，对于每一个E点的位置，再三分F点的位置。
（细节注意：由于答案要保留小数点后两位，而地图的最大大小为1000，经过测试，1000乘于2/3大概乘那么30次就可以变得比0.01小，所以我们的三分大概只需要循环30次就可以了。不过我为了安全，循环了40次，反正没差多少。因此，E点需要三分40次，对于每一个E点，需要三分F点40*2次，大概就320次的样子。）
>事实上，这道题除了用三分的做法之外，好像还有什么其他做法，比如模拟退火算法， 但是我还没有学过。
AC代码如下

 #include<cstdio>
 #include<cmath>
 using namespace std;
 struct point
 {
 double x,y;
 point()
 {
 x=y=;
 }
 };
 double m_abs(double a)
 {
 return a<?-a:a;
 }
 int main()
 {
 point a,b,c,d;
 scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y,&d.x,&d.y);
 double p,q,r;
 scanf("%lf%lf%lf",&p,&q,&r);
 double result=100000000.0;
 point S1=a,S2=b,E1=c,E2=d;
 for(int i=;i<=;i++)
 {
 point s1,s2;
 s1.x=S1.x+(S2.x-S1.x)/3.0;
 s1.y=S1.y+(S2.y-S1.y)/3.0;
 s2.x=S2.x-(S2.x-S1.x)/3.0;
 s2.y=S2.y-(S2.y-S1.y)/3.0;
 double T1,T2;
 double X,Y;
 X=m_abs(a.x-s1.x);
 Y=m_abs(a.y-s1.y);
 T1=sqrt(X*X+Y*Y)/p;
 X=m_abs(a.x-s2.x);
 Y=m_abs(a.y-s2.y);
 T2=sqrt(X*X+Y*Y)/p;
 E1=c;E2=d;
 double T3=10000000.0,T4=100000000.0;
 for(int j=;j<=;j++)
 {
 double t1,t2;
 point e1,e2;
 e1.x=E1.x+(E2.x-E1.x)/3.0;
 e1.y=E1.y+(E2.y-E1.y)/3.0;
 e2.x=E2.x-(E2.x-E1.x)/3.0;
 e2.y=E2.y-(E2.y-E1.y)/3.0;
 X=m_abs(s1.x-e1.x);
 Y=m_abs(s1.y-e1.y);
 t1=sqrt(X*X+Y*Y)/r;
 X=m_abs(s1.x-e2.x);
 Y=m_abs(s1.y-e2.y);
 t2=sqrt(X*X+Y*Y)/r;
 X=m_abs(d.x-e1.x);
 Y=m_abs(d.y-e1.y);
 t1+=sqrt(X*X+Y*Y)/q;
 X=m_abs(d.x-e2.x);
 Y=m_abs(d.y-e2.y);
 t2+=sqrt(X*X+Y*Y)/q;
 if(t1>=t2)
 {
 E1=e1;
 T3=t2<T3?t2:T3;
 }
 else
 {
 E2=e2;
 T3=t1<T3?t1:T3;
 }
 }
 E1=c;E2=d;
 for(int j=;j<=;j++)
 {
 double t1,t2;
 point e1,e2;
 e1.x=E1.x+(E2.x-E1.x)/3.0;
 e1.y=E1.y+(E2.y-E1.y)/3.0;
 e2.x=E2.x-(E2.x-E1.x)/3.0;
 e2.y=E2.y-(E2.y-E1.y)/3.0;
 X=m_abs(s2.x-e1.x);
 Y=m_abs(s2.y-e1.y);
 t1=sqrt(X*X+Y*Y)/r;
 X=m_abs(s2.x-e2.x);
 Y=m_abs(s2.y-e2.y);
 t2=sqrt(X*X+Y*Y)/r;
 X=m_abs(d.x-e1.x);
 Y=m_abs(d.y-e1.y);
 t1+=sqrt(X*X+Y*Y)/q;
 X=m_abs(d.x-e2.x);
 Y=m_abs(d.y-e2.y);
 t2+=sqrt(X*X+Y*Y)/q;
 if(t1>=t2)
 {
 E1=e1;
 T4=t2<T4?t2:T4;
 }
 else
 {
 E2=e2;
 T4=t1<T4?t1:T4;
 }
 }
 T1+=T3;
 T2+=T4;
 if(T1>=T2)
 {
 S1=s1;
 result=T2<result?T2:result;
 }
 else
 {
 S2=s2;
 result=T1<result?T1:result;
 }
 }
 printf("%.2f\n",result);
 return ;
 }

话说这个还是我第一次使用三分呢，以前都没有用过。