图的遍历---------开始开始-------o(∩_∩)o 哈哈

图的遍历

深度优先搜索(Depth First Search , DFS)　　

　　--深度优先搜索--我的理解就是分身术的另一种实现方法---用分身术将所有能看到的路都走一遍----这就是深度搜索---

下面给一个图  让大家理解一下

void DFS(Vertex V)  //深度优先搜索的伪码描述
{
    visited[V]=ture;  //先点亮这个节点的灯
    for(V的每个临节点 W)  //站在V的位置  所有能看到的灯 W
        if(!Visited[W])//如果没有亮
        DFS(W);//走到这个灯的位置递归的点亮(递归确实很难理解,但是在前面我已经给了两个训练递归思想的代码,你还记得么?)
}   //不得不说  虽然递归十分耗费内存但是递归确实 很好用.

越看感觉越想   树的先序遍历,有木有?    递归的思想是一样的(你在树那里的遍历方法有几种这里可以用不?)

----------前面咱们说了两种----图的储存方式----

下面来说一下不同的储存方式 , 用于搜索带来的不同效果.

若有N个节点,E条边 , 时间复杂度是

　　·　　用邻接矩阵储存图,有O(N+E)     //  如果用邻接矩阵的话 在这个算法当中相当于  每个节点 每条边都走了一次.

　　·　　用邻接矩阵储存图 , 有O(N^2)  //这个怎么说呢 自己想想

void DFS(Vertex V)  //深度优先搜索的伪码描述
{
    visited[V]=ture;  //先点亮这个节点的灯
    for(V的每个临节点 W)  //站在V的位置  所有能看到的灯 W
        if(!Visited[W])//如果没有亮
        DFS(W);//走到这个灯的位置递归的点亮(递归确实很难理解,但是在前面我已经给了两个训练递归思想的代码,你还记得么?)
}   //不得不说  虽然递归十分耗费内存但是递归确实 很好用.

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------------------------今天听鹏哥说了一上午  也算复习   也算预习    也有收获   ------------

深度优先搜索,就是找一条线  向下面  一直搜  ,,,而广度优先搜索是     从一个点开始  向外面慢慢的扩散------

下面附上广搜的相关.

广度优先搜索(Breadth First Search ,,BFS)

从根节点出发,从上到下 ,从左到右-------具体的实现是借助一个队列---这个前面咱们将堆的时候好像说过.

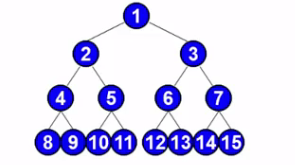走过的顺序就是这个

void BFS(Vertex V)  //树的根节点
{
    visited[V]=ture;   //访问 上面传下来的根节点  并且标记为已访问
    Enqueue(V,Q);          //将 V 压进队列里面
    while(IsEmpty[Q])          //判断队列是否为空
    {
        V=Dequeue(Q);         //出队列   并且赋值给V
        for(V的每个临节点W)         //V访问 V的每个临节点
        {
            if(!visited[W])    //如果已经访问  就算了  否则进去,
            {
                visited[w]=ture;
                Enqueue(W,Q);   //将刚才被删除的元素的   儿子压进去.
            }
        }
    }
}

邻接矩阵 时间复杂度为  N^2     然而邻接表的时间复杂度是  N+E  思考一下  why?

-----------------------下面开始说  --两种不同的遍历   分别适用的方向.----下面附上一个   大侠走迷宫.-----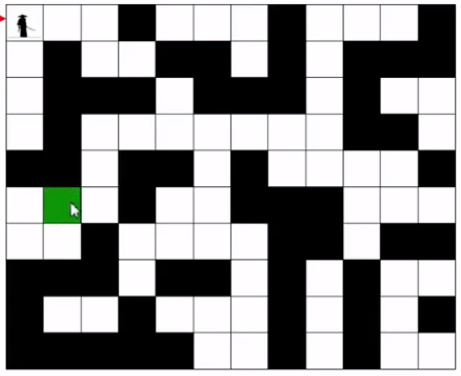

给大侠一点规定------大侠喜欢  从十二点方向开始,按照顺时针的方法走路口---------

这时候大侠走出迷宫的  所需要经过的  格子就很多了

如果大侠  按照广搜的方法   仍然   十二点顺时针 是什么情况?

-------------------------不挨着的节点怎么----图不连通?----那还遍历个什么呀?----------------------

连同: 如果从V到W存在一条(无向)路径,则称V和W是连通的.

路径:V到W的路径是一系列顶点{V,v1,v2,v3,...,vn,W}的集合其中任一一对相邻的顶点间都有图中的边.路径的长度是路径中的变数(如果带权的话,则是各边的权重之和) .  如果从V到W之间的所有顶点都不同则成为简单路径.

回路:起点等于终点的路径,  (V ,v1,v2,v3,V           这就是一个回路).

连通图:图中任意两顶点均连通.

图不连通怎么办?

连通分量:无向图的极大连同子图 　　　　　　(好好理解慢慢看).

　　极大顶点数:再加一个顶点就不联通了.

　　极大边数:包含子图中所有顶点相连的所有边.

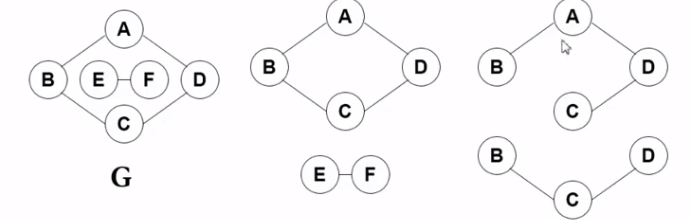
G是原图  后面的四个就是无向图G的极大连同子图  从上到下  从左到右的顺序开始说.

第一个 符合上述两点   第二个也符合

第三个  不符合第二点         第四个  不符合第一点

------------------------------------------------------------------------------------------------

下面说说  有向图   有向图分为强连同和弱连同

强连同:有向图中顶点V,W之间存在双向路径,则称V,和W是强连同的.(意思就是说  我也已从V 到W  也可以从W到V  其中不需要必须走同一条路)

强连通图:有向图中任意两顶点均强连同.

强连通分量:有向图的极大强连同子图.

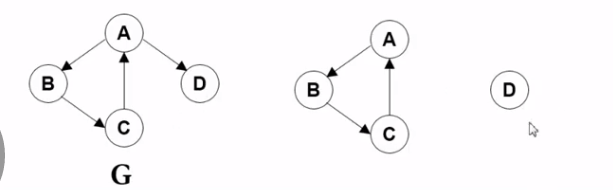
图G的极大强连同子图有两个          第一个  任意两点都可以连同 并且 再多一个 就不行了   第二个      也是

void DFS(Vertex V)             //最终将所有连通的都  遍历了.
{
    visited[V]=ture;
    for(V的每个节点W)
        if(!visited[w])
        DFS(W);
}
/*不连通的怎么遍历呢?*/
void ListComponents(Graph G)
{
    for(each V in G)      //向下输送所有的 不连通分量
        if(!visited[v])
    {
        DFS(v);   //  or BFS[v];
    }
}

拯救007......007被   困在了一个孤岛上面    湖里面都是鳄鱼   英勇的零零七 决定一  鳄鱼头当成  跳板跳到河岸上面下面附图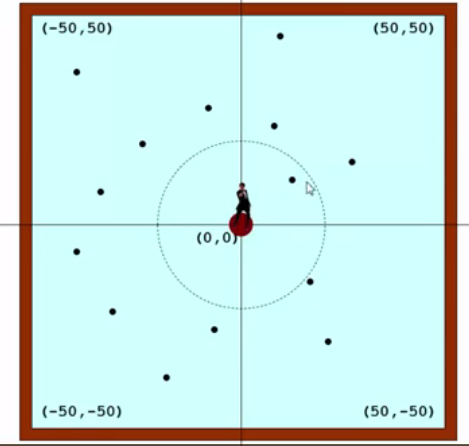

这一道题 深度优先   和广度优先 都可以  但是 根据实际问题来看  深度优先 可能更好一点.

我们在上面第一个程序上做一个 修改.

void Save007(Graph G)
{
    for(each V in G)  //孤岛上面的 所有相邻的  岛一个一个试  知道 跳出去.
    {
        if(!visited[V]&&FirstJumpe[V])  //没有跳过 并且 第一跳可以跳出.
        {
            answer=DFS[v];
        }
    }
    if(answer==YEs)
        output("Yes");
    else
        output("NO");
}