算法导论 第三章 and 第四章

第三章

渐进的基本O（）....

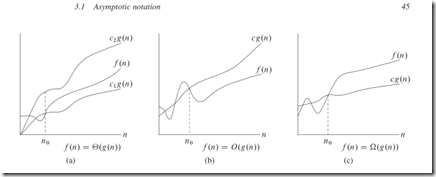
常用函数

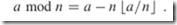
% 和  // 转换

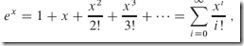
斯特林近似公式

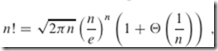
斐波那契数

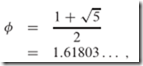
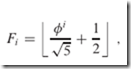
第四章

分治策略：分解（递归）--解决（递归触底）--合并

求解递归式的3种方法：

1：代入法（替代法）：猜测一个（靠经验）--数学归纳法

·2：递归树法：画树p31【第3版中文】p51->递归式--证明

3：主方法：

快速，有些地方不能涉及，递归式不易写出

4.1最大数组问题

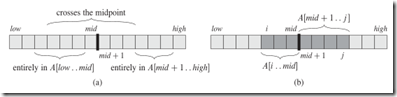
分治法：

1.A[low ，mid]  2.A[mid+1, high] 3.包含mid中间（想左和右分别遍历组合找出最大）

import decimal

def FIND_MAX_CROSSING_SUBARRAY(A,low,mid,high):

    left_sum =  decimal.MIN_EMIN

    sum = 0

    for i in range(mid,low - 1,-1):

        sum = sum + A[i]

        if sum > left_sum:

            left_sum = sum

            max_left = i

    right_sum = decimal.MIN_EMIN

    sum = 0

    for i in range(mid + 1,high+1):

        sum = sum + A[i]

        if sum > right_sum:

            right_sum = sum

            m   ax_right = i

    return (max_left,max_right,left_sum + right_sum)    

def FIND_MAXIMUM_SUBARRAY(A,low,high):

    if high == low:

        return (low,high,A[low])

    else:

        mid = (low + high) //2

        (left_low,left_high,left_sum) = FIND_MAXIMUM_SUBARRAY(A,low,mid)

        (right_low,right_high,right_sum) = FIND_MAXIMUM_SUBARRAY(A,mid+1,high)

        (cross_low,cross_high,cross_sum) = FIND_MAX_CROSSING_SUBARRAY(A,low,mid,high)

        if left_sum >= right_sum and left_sum >= cross_sum:

            return (left_low,left_high,left_sum)

        elif right_sum >= left_sum and right_sum >= cross_sum:

            return (right_low,right_high,right_sum)

        else:

            return (cross_low,cross_high,cross_sum)

if __name__ == '__main__':

    A = [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]

    temp = FIND_MAXIMUM_SUBARRAY(A,0,len(A)-1)

    print(temp)

'''

========= RESTART: F:/python/algorithms/4_1_find_maximum_subarray.py =========

(7, 10, 43)

O（n*n）

python 3.5.1

win7

和伪代码几乎一模一样 - -！

唯一要注意的问题还是 python 从0开始

'''

 

线性级改进

O（n）

习题：4.1-5

很容易理解，当我们加上一个正数时，和会增加；当我们加上一个负数时，和会减少。如果当前得到的和是个负数，那么这个和在接下来的累加中应该抛弃并重新清零，不然的话这个负数将会减少接下来的和

def FindGreatestSumOfSubArray(A):

        if A :

                nCurSum = nGreatestSum = 0

                #nCurSum 保存现在和 nCreatestSum 保存最大的

                curStart = curEnd = 0

                start = end = 0

                for i in range(len(A)): #遍历A

                        nCurSum += A[i]

                        curEnd = i

                        if nCurSum < 0: #为负数摒弃 加一个正数=把正数减

小

                                nCurSum = 0

                                curStart = curEnd = i + 1

                        if nCurSum > nGreatestSum: #刷新最大数组

                                nGreatestSum = nCurSum

                                start = curStart

                                end = curEnd

                #都是负数 遍历找最大负数

                if nGreatestSum == 0:

                        nGreatestSum = A[0]

                        start = end = 0

                        for i in range(1,len(A)):

                                if A[i] > nGreatestSum:

                                        nGreatestSum = A[i]

                                        start = end = i

                return [start,end,nGreatestSum]

        else:

                return []

if __name__ =="__main__":

        A =  [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]

        temp = FindGreatestSumOfSubArray(A)

        print(temp)

'''

$ python3 4_1_5_find_maximum_subarray.py 

[7, 10, 43]

O（n）

Python 3.4.3+

Ubuntu 15.10

'''

 

参考引用：http://www.wutianqi.com/?cat=515&paged=6

http://www.cnblogs.com/chinaxmly/archive/2012/10/10/2718621.html

http://blog.csdn.net/yelbosh/article/details/7558981