微信小程序引入外部js 方法

步骤：

1.首先将外部js放在你指定的文件夹里（这都是废话。。。）

2.接下来 将该js文件中你要使用的方法给暴露出来

3.在您要使用的js中引入该js

4.使用暴露出来的方法

例子：使用md5加密

首先将md5.js放入项目里某个文件夹中（我这里放在了utils工具文件夹中）

打开md5.js ，将我要使用的方法用module.exports给暴露出来，如图所示（我这里暴露了三个方法，用的json形式，若只有一个就直接写，不用使用json）

在您想要用到这个方法的js里面 require这个js，然后调用即可

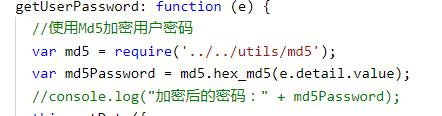
ps:这里需要注意的是路径问题，使用相对路径，如果出现报错 undefined，改一下相对目录层及，一个../不行就使用两个（）。