P2453 [SDOI2006]最短距离 dp

自己想出来了!这个dp比较简单,而且转移也很简单,很自然,直接上代码就行了.

题干:

一种EDIT字母编辑器，它的功能是可以通过不同的变换操作可以把一个源串X [l..m]变换为新的目标串y[1..n]。EDIT提供的变换操作有：

源串中的单个字符可被删除(delete)；

被替换 (replace)；

被复制到目标串中去(copy)；

字符也可被插入(insert)；

源串中的两个相邻字符可进行交换并复制到目标串中去(twiddle)；

在完成其它所有操作之后，源串中余下的全部后缀就可用删至行末的操作删除(kill)。

例如，将源"algorithm"转换成目标串"altruistic"的一种方法是采取下面的操作序列:

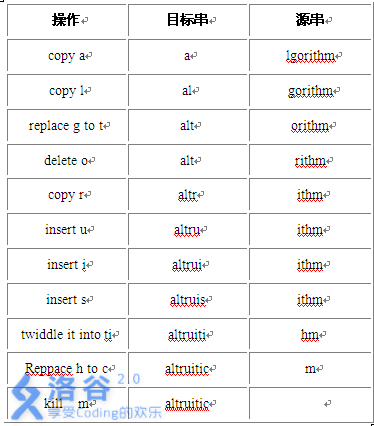
要达到这个结果还可能有其它一些操作序列。

操作delete,replace，copy，insert，twiddle和kill中每一个都有一个相联系的代价cost。例如

cost(delete)=3;
cost(replace)=6;
cost(copy)=5;
cost(insert)=4;
cost(twiddle)=4;
cost(kill)=被删除的串长*cost(delete)-1;

一个给定的操作序列的代价为序列中各操作代价之和。 例如上述操作序列的代价为

3*cost(copy)+2*cost(replace)+cost(delete)+3*cost(insert) + cost(twiddle) +cost(kill)

=3*5+2*6+3+3*4+4+1*3-1=48

编程任务：

给定两个序列x[1..m],y[1..n]和一些操作代价集合，X到Y的最短距离为将X转化为Y的最小的转换序列的代价。请给出一个算法来找出x[1..m]至y[1..n]的最短距离。

输入输出格式

输入格式：

第一行：源序列x[1..m]。（m<200）

第二行：目标序列y[1..n]。(n<200)

第三行：5个正整数（<100）：分别是：delete 、replace 、copy、 insert、 twiddle的代价。

输出格式：

X到Y的最短距离（最小代价和）。

输入输出样例

输入样例#1： 复制

algorithm
altruistic
3 6 5 4 4

输出样例#1： 复制

48

代码:

#include<iostream>
#include<cstdio>
#include<cmath>
#include<ctime>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
#define duke(i,a,n) for(int i = a;i <= n;i++)
#define lv(i,a,n) for(int i = a;i >= n;i--)
#define clean(a) memset(a,0,sizeof(a))
const int INF =  << ;
typedef long long ll;
typedef double db;
template <class T>
void read(T &x)
{
    char c;
    bool op = ;
    while(c = getchar(), c < '' || c > '')
        if(c == '-') op = ;
    x = c - '';
    while(c = getchar(), c >= '' && c <= '')
        x = x *  + c - '';
    if(op) x = -x;
}
template <class T>
void write(T x)
{
    if(x < ) putchar('-'), x = -x;
    if(x >= ) write(x / );
    putchar('' + x % );
}
int n,m;
char x[],y[];
int del,rep,cop,ins,twi;
int f[][];
int main()
{
    scanf("%s",x + );
    scanf("%s",y + );
    n = strlen(x + );
    m = strlen(y + );
    read(del);read(rep);read(cop);
    read(ins);read(twi);
    memset(f,,sizeof(f));
    f[][] = ;
    duke(i,,m)
    f[i][] = i * ins;
    duke(i,,n)
    f[][i] = i * del;
    duke(i,,m)
    {
        duke(j,,n)
        {
            f[i][j] = min(f[i][j],f[i - ][j] + ins);
            f[i][j] = min(f[i][j],f[i - ][j - ] + rep);
            if(y[i] == x[j])
            f[i][j] = min(f[i][j],f[i - ][j - ] + cop);
            if(i >  && j >  && y[i - ] == x[j] && y[i] == x[j - ])
            f[i][j] = min(f[i][j],f[i - ][j - ] + twi);
            f[i][j] = min(f[i][j],f[i][j - ] + del);
        }
    }
    int minn = INF;
    duke(i,,n - )
        minn = min(minn,f[m][i] + (n - i) * del - );
    minn = min(minn,f[m][n]);
    printf("%d\n",minn);
    return ;
}
/*
algorithm
altruistic
3 6 5 4 4
*/