cf711E ZS and The Birthday Paradox

ZS the Coder has recently found an interesting concept called the Birthday Paradox. It states that given a random set of 23 people, there is around 50% chance that some two of them share the same birthday. ZS the Coder finds this very interesting, and decides to test this with the inhabitants of Udayland.

In Udayland, there are 2ⁿ days in a year. ZS the Coder wants to interview k people from Udayland, each of them has birthday in one of 2ⁿ days (each day with equal probability). He is interested in the probability of at least two of them have the birthday at the same day.

ZS the Coder knows that the answer can be written as an irreducible fraction 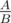. He wants to find the values of A and B (he does not like to deal with floating point numbers). Can you help him?

Input

The first and only line of the input contains two integers n and k (1 ≤ n ≤ 10¹⁸, 2 ≤ k ≤ 10¹⁸), meaning that there are 2ⁿ days in a year and that ZS the Coder wants to interview exactly k people.

Output

If the probability of at least two k people having the same birthday in 2ⁿ days long year equals 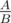(A ≥ 0, B ≥ 1, 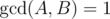), print the A and B in a single line.

Since these numbers may be too large, print them modulo 10⁶ + 3. Note that A and B must be coprime before their remainders modulo 10⁶ + 3 are taken.

Examples

Input

3 2

Output

1 8

Input

1 3

Output

1 1

Input

4 3

Output

23 128

Note

In the first sample case, there are 2³ = 8 days in Udayland. The probability that 2 people have the same birthday among 2 people is clearly , so A = 1, B = 8.

In the second sample case, there are only 2¹ = 2 days in Udayland, but there are 3 people, so it is guaranteed that two of them have the same birthday. Thus, the probability is 1 and A = B = 1.

想要知道答案是啥还是很容易的，用高中知识即可知道1 - {  A(2^n,k) / 2^(nk)  } 即是所求，A(a,b)是排列数。

问题是要先化简再上下同时取模

可以先证明如果有大数A、B，假设(A%mod)/(B%mod)==p/q，那么1-A/B=(B-A)/B=(q-p)/q。(在模mod意义下)

所以只要知道A(2^n,k)/2^(nk)，就能知道答案了

先化简。

分式下面只有2，所以gcd=2^t，t不知道，但是显然t是由上面A(2^n,k)决定。

考虑(2^n)(2^n-1)...(2^n-k+1)有多少个因子2。如果把2^n单独考虑，剩下(2^n-1)...(2^n-k+1)的2的因子数跟1~k-1的2的因子数一样多。因为任取个(2^n-s),它能和s对应

所以因子数就是n+(k-1)/2+(k-1)/4+...+(k-1)/2^p，除到(k-1)/2^p=0为止

得到了gcd=2^t的t之后，只要上下同时乘(2关于mod的逆元)乘t次，就完成了化简。

然后注意到当k>=mod时，(2^n)(2^n-1)(2^n-mod+1)%mod==0，由鸽巢原理这是显然的。

所以当k<mod，A(2^n,k)%mod暴力算，k>=mod，A(2^n,k)%mod==0。

而2^(nk)%mod是容易算的。

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<set>
 #include<map>
 #include<ctime>
 #define LL long long
 #define inf 0x7ffffff
 #define pa pair<int,int>
 #define mkp(a,b) make_pair(a,b)
 #define pi 3.1415926535897932384626433832795028841971
 #define mod 1000003
 using namespace std;
 inline LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 LL n,k;
 LL rev_2;
 LL bit[];
 inline LL quickpow(LL a,LL b,LL MOD)
 {
     LL s=;
     while (b)
     {
         if (b&)s=(s*a)%MOD;
         a=(a*a)%MOD;
         b>>=;
     }
     return s;
 }
 int main()
 {
     rev_2=quickpow(,mod-,mod);bit[]=;for (int i=;i<;i++)bit[i]=bit[i-]<<;
     n=read();k=read();
     if (n<=&&k>bit[n]){puts("1 1");return ;}
     if (k==){puts("0 1");return ;}
     LL mx=quickpow(,n,mod),now=mx;
     LL ans1=,ans2=;
     LL te=k-,sum=n;
     while (te)
     {
         sum+=te/;
         te>>=;
     }
     LL sv=k;
     for (LL i=;i<=min(sv,(LL)mod);i++)
     {
         k--;
         ans2=(ans2*mx)%mod;
         ans1=(ans1*now)%mod;
         now--;if (!now)now+=mod;
     }
     while (k%(mod-)!=)ans2=(ans2*mx)%mod,k--;
     ans1=(ans1*quickpow(rev_2,sum,mod))%mod;
     ans2=(ans2*quickpow(rev_2,sum,mod))%mod;
     printf("%lld %lld\n",(ans2-ans1+mod)%mod,ans2);
     //ans=1-{ (2^n*(2^n-1)*(2^n-2)*...*(2^n-k+1))/(2^n)^k }
 }

cf 711E