Lucas 卢卡斯定理

Lucas：

卢卡斯定理说白了只有一条性质

$$ C^n_m \equiv C^{n/p}_{m/p} \times C^{n \bmod p}_{m \bmod p} \ (mod \ \ p) $$

用于 m，n 很大时快速求组合数。（p 为质数）

CODE：

 long long Lucas(long long n,long long m){
     if(m==)return ;
     if(n<m)return ;
     if(n<p&&m<p)return fac[n]*inv[n-m]%p*inv[m]%p;
     return Lucas(n/p,m/p)*Lucas(n%p,m%p)%p;
 }

证明：

前置技能：二项式定理

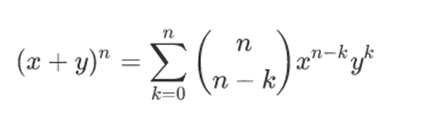
对于任意质数p，根据费马小定理有：

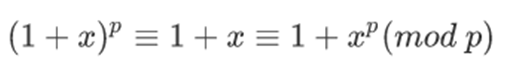
然后我们把(1+x)^n这个式子处理一下：

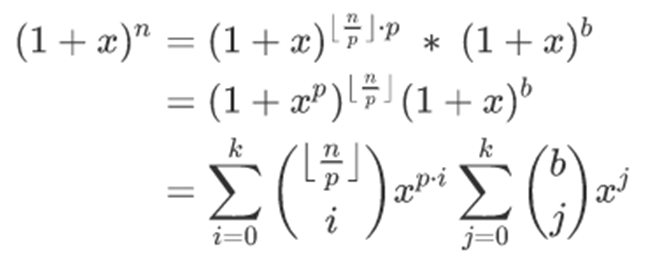
然后同时我们还有：

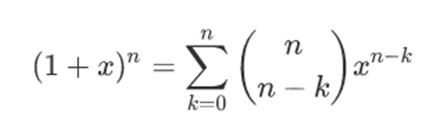
观察一下两个式子x的m次方的系数，可以得到：

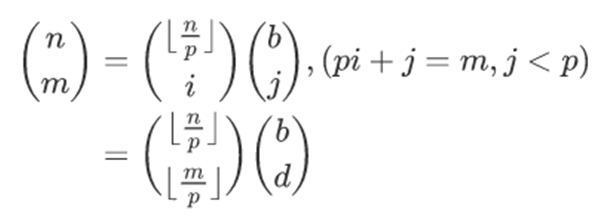
然后我们回到最开始的递归形式的那个式子，会发现…… 就证完了OvO

( 引用自 hy 大佬课件)