Number of Containers ZOJ - 3175（数论题）

Problem Description

For two integers m and k, k is said to be a container of m if k is divisible by m. Given 2 positive integers n and m (m < n),

the function f(n, m) is defined to be the number of containers of m which are also no greater than n.

For example, f(5, 1)=4, f(8, 2)=3, f(7, 3)=1, f(5, 4)=0...Let us define another function F(n) by the following equation:

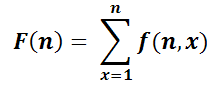
Now given a positive integer n, you are supposed to calculate the value of F( n).

Input

There are multiple test cases. The first line of input contains an integer T(T<=200) indicating

the number of test cases. Then T test cases follow.Each test case contains a positive integer n (0 <n <= 2000000000) in a single line.

Output

For each test case, output the result F(n) in a single line.

Sample Input

1
4     

Sample Output

4

题目大意：

求 n/i-1；（0<i<n）的和，，，，由于数据高达20亿●﹏●，所以，暴力就会T！！！

思路：

画图，画出函数图像：y = n/x，以 y = x对称可以用 横坐标表示i 从该点画一条垂直的线

这条线上的所有整数点的个数就是 n/i那么n/1+n/2+n/3+……n/(n-2)+n/(n-1)+n/n（有点像调和级数哦じò ぴé）

可以表示为i*(n/i)=n这条线答案就是这条线与坐标轴围成的面积内的整数点的个数画一条x=y的线与xy=n相交

可以知道面积关于 x=y 对称我们只需求n/1+n/2+n/3+……求到k=sqrt(n)处（1个梯形）

之后乘以2（得到2个梯形的面积 其中有一个正方形的区域是重复的）减去重复的区域k*k个

就可以用这个方法，也可以用来快速求（n/1+n/2+n/3+…+n/n）。

参考代码：

#include<iostream>
#include<cmath>
using namespace std;
#define ll long long
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll n,sum=;
        cin>>n;
        int m=sqrt(n);
        for(int i=;i<=m;i++)
            sum+=n/i;
        sum*=;
        sum=sum-m*m-n;
        cout<<sum<<endl;
    }
    return ;
}