Stanford NLP 课堂笔记之正则表达式

1.[]表达式的用法

正则表达式可以让我们匹配我们想要的字符串形式，增加了效率，在自然语言处理领域有较大的作用。

模式	匹配
[Ww]oodchuck	Woodchuck,woodchuck
[1234567890]	Any digit

如上面所用的模式既是正则表达式中的常用语法，在“[]”内部的字母表示可以匹配其中的任一字母，

[A-Z]表示大写字母，[a-z]表示小写字母，[0-9]表示数字，[A-Za-z]表示大写加小写字母，

2.特别字符的用法

模式	含义	匹配
colou?r	匹配前面表达式0次或1次	color,colour
oo*h!	匹配前面表达式0至无穷次	oh!,ooh!,oooh!
o+h!	匹配前面表达式1至无穷次	oh!,ooh!,oooh!
beg.n	匹配任意字母	begin,beghn
a|b|c	a/b/c	a,b,c

在正则表达式中还有两个表示位置的符号，分别是"^"和"$"，代表开头和结尾。

^[A-Z]匹配首字母大写的字符串，如

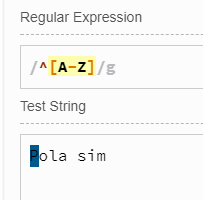
.$则表示匹配字符串的最后一个任意字母，演示如下

3.示例

下面是一个我们要匹配出所有的the的过程。

当我们直接用the进行匹配时发现出现了两个错误，一个是没有把大写的The匹配进来（准确率），还有一个是把there中的前三个字母误当成了the（召回率）。

对正则表达式进行修改

这样成功的把所有的the匹配出来了，但是召回率依旧没有提高，继续修改

[^A-Za-z]表示匹配不属于这个合集的字符。