最近公共祖先 LCA (Lowest Common Ancestors)-树上倍增

树上倍增是求解关于LCA问题的两个在线算法中的一个，在线算法即不需要开始全部读入查询，你给他什么查询，他都能返回它们的LCA。

树上倍增用到一个关键的数组F[i][j],这个表示第i个结点的向上2^j层的结点。在RMQ-ST中用救是这样的数组。

在树上倍增中也是关键点。

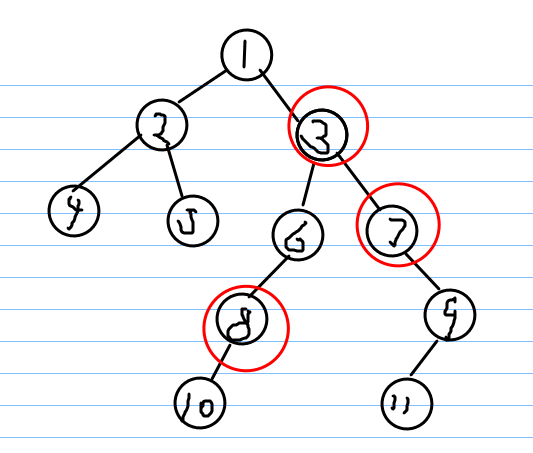
如在上图中，我们要找结点8和7的LCA，从途中我们可以看出是3(这句估计是废话)。采用倍增的思想是这样的

首相判断结点U和V是否在同一层次，即是否深度相同。因为在深度相同后这样后，二者就可以同时向上跳某n层，去识别所到之点是否为它们的LCA。

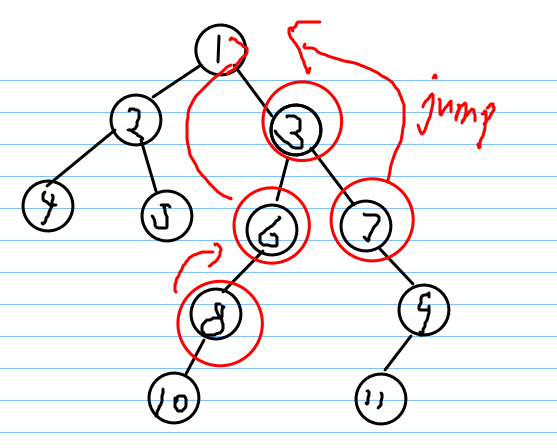
如果深度较大(在底下的点)，跳到较高的那个点后，发现二者重合了，那么恭喜，LCA已经找到了

另外底下的结点向上跳的步数也不是一步一层的，要不然太慢了。而是计算出U和V的高度差，按高度差的对数k(2^k)去跳，因而越来越接近高层结点，直到相等。

 if(depth[u] < depth[v])
     {
         swap(u,v);//始终让U在最小边，便于理解
     }
     while(depth[u] != depth[v])//二者不再同一高度
     {
         u = father[u][lg[ depth[u]-depth[v]]]; //u向上跳 2^(二者高度差的对数)层
     }
     if(u==v)//重叠直接就是找到LCA
     {
         return u;
     }

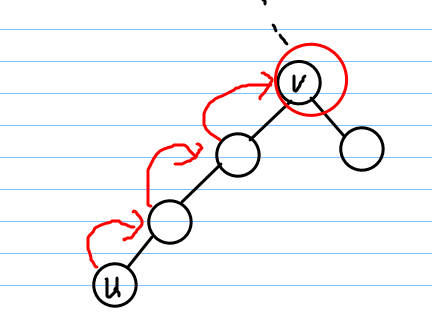
但是大多数情况不是这样的，它们往往不会重合，因此要开是同步向上跳。

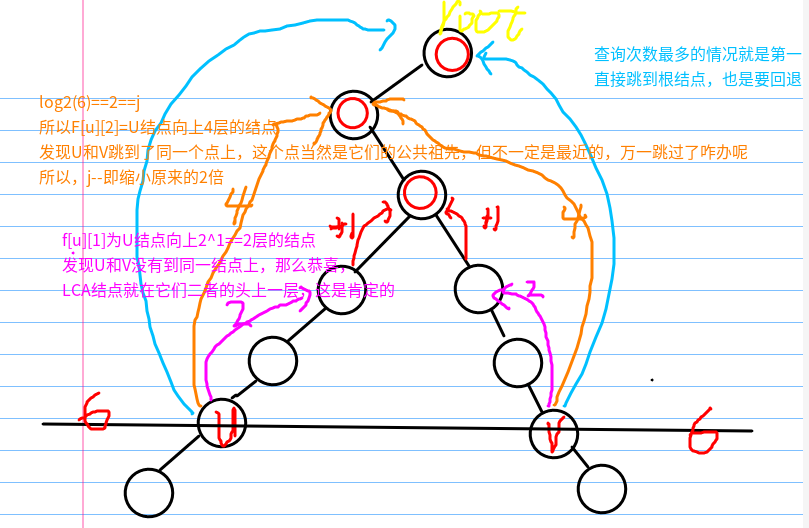
以U结点到根结点的距离(U的深度为基准)，取对数后为k，在这样去跳2^k层是肯定不会超过根上面的

但这样不保证是否错过了LCA，所以回退,k-1,重新跳2^(k-1)层，再去判断。直到U和V不等时，它们上一层的结点一定就是LCA了。再举个简单的例子吧

 for(int j =lg[depth[u]];j>=;j--)//lg[depth[u]]表示u距离根结点的距离取对数
     {
         if(father[u][j] != father[v][j])//直到二者所跳的地方不一样
         {
             u = father[u][j];
             v = father[v][j];
         }
     }
     return father[u][];//返回u的father/上一层结点就是LCA

这个LCA需要以构建好树和计算出每个结点的深度的条件为基础的。

dfs就不细说了，这里只说一下这个语句

  father[curnode][j] = father[father[curnode][j-]][j-];

模板题传送门