POJ - 1149 PIGS （建图思维+最大流）

（点击查看原题）

题目分析

（以下均为 Edelweiss 大佬的思路，博主承认自己写不了这么好，但是学习的心促使我记录下这个好题的写法，所以代码是我写的）

【题目大意】 有 M 个猪圈，每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。依 次来了 N 个顾客，每个顾客分别会打开指定的几个猪圈，从中买若干头猪。每 个顾客分别都有他能够买的数量的上限。每个顾客走后，他打开的那些猪圈中的 猪，都可以被任意地调换到其它开着的猪圈里，然后所有猪圈重新关上。问总共 最多能卖出多少头猪。（1 <= N <= 100, 1 <= M <= 1000）

举个例子来说。有 3 个猪圈，初始时分别有 3、1 和 10 头猪。依次来了 3 个顾客， 第一个打开 1 号和 2 号猪圈，最多买 2 头；第二个打开 1 号和 3 号猪圈，最多买 3 头；第三个打开 2 号猪圈，最多买 6 头。那么，最好的可能性之一就是第一个 顾客从 1 号圈买 2 头，然后把 1 号圈剩下的 1 头放到 2 号圈；第二个顾客从 3 号圈买 3 头；第三个顾客从 2 号圈买 2 头。总共卖出 2+3+2=7 头。

【建模方法】 不难想象，这个问题的网络模型可以很直观地构造出来。就拿上面的例子来说， 可以构造出图 1 所示的模型（图中凡是没有标数字的边，容量都是∞）：

• 三个顾客，就有三轮交易，每一轮分别都有 3 个猪圈和 1 个顾客的结点。
• 从源点到第一轮的各个猪圈各有一条边，容量就是各个猪圈里的猪的初始 数量。
• 从各个顾客到汇点各有一条边，容量就是各个顾客能买的数量上限。
• 在某一轮中，从该顾客打开的所有猪圈都有一条边连向该顾客，容量都是 ∞。
• 最后一轮除外，从每一轮的 i 号猪圈都有一条边连向下一轮的 i 号猪圈， 容量都是∞，表示这一轮剩下的猪可以留到下一轮。
• 最后一轮除外，从每一轮被打开的所有猪圈，到下一轮的同样这些猪圈， 两两之间都要连一条边，表示它们之间可以任意流通。

这个网络模型的最大流量就是最多能卖出的数量。图中最多有 2+N+M×N≈100,000 个结点。这个模型虽然很直观，但是结点数太多了，计算速 度肯定会很慢。其实不用再想别的算法，就让我们继续上面的例子，用合并的方 法来简化这个网络模型。

首先，最后一轮中没有打开的猪圈就可以从图中删掉了，也就是图 2 中红色 的部分，显然它们对整个网络的流量没有任何影响。

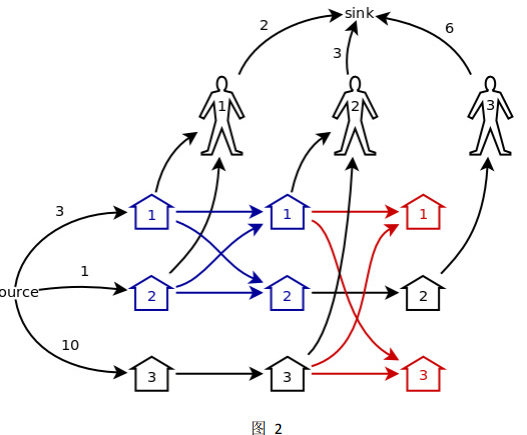
接着，看图 2 中蓝色的部分。根据我总结出的以下几个规律，可以把这 4 个 点合并成一个：

规律 1. 如果几个结点的流量的来源完全相同，则可以把它们合并成一个。

规律 2. 如果几个结点的流量的去向完全相同，则可以把它们合并成一个。

规律 3. 如果从点 u 到点 v 有一条容量为∞的边，并且点 v 除了点 u 以外没 有别的流量来源，则可以把这两个结点合并成一个。

根据规律 1，可以把蓝色部分右边的 1、2 号结点合并成一个；根据规律 2， 可以把蓝色部分左边的 1、2 号结点合并成一个；最后，根据规律 3，可以把蓝 色部分的左边和右边（已经分别合并成了一个结点）合并成一个结点。于是，图 2 被简化成了图 3 的样子。也就是说，最后一轮除外，每一轮被打开的猪圈和下 一轮的同样这些猪圈都可以被合并成一个点。

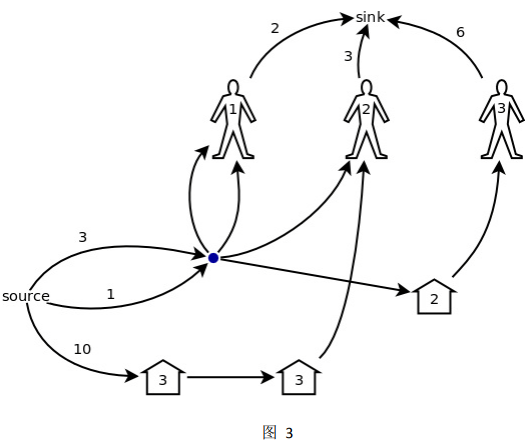
接着，根据规律 3，图 3 中的蓝色结点、2 号猪圈和 1 号顾客这三点可以合 并成一个；图 3 中的两个 3 号猪圈和 2 号顾客也可以合并成一个点。当然，如果 两点之间有多条同向的边，则这些边可以合并成一条，容量相加，这个道理很简 单，就不用我多说了。最终，上例中的网络模型被简化成了图 4 的样子。

让我们从上图 中重新总结一下构造这个网络模型的规则：

• 每个顾客分别用一个结点来表示。
• 对于每个猪圈的第一个顾客，从源点向他连一条边，容量就是该猪圈里的 猪的初始数量。如果从源点到一名顾客有多条边，则可以把它们合并成一 条，容量相加。
• 对于每个猪圈，假设有 n 个顾客打开过它，则对所有整数 i∈[1, n)，从该 猪圈的第 i 个顾客向第 i + 1 个顾客连一条边，容量为∞。
• 从各个顾客到汇点各有一条边，容量是各个顾客能买的数量上限

拿我们前面一直在讲的例子来说：1 号猪圈的第一个顾客是 1 号顾客，所以 从源点到 1 号顾客有一条容量为 3 的边；1 号猪圈的第二个顾客是 2 号顾客，因 此从 1 号顾客到 2 号顾客有一条容量为∞的边；2 号猪圈的第一个顾客也是 1 号 顾客，所以从源点到 1 号顾客有一条容量为 1 的边，和之前已有的一条边合并起 来，容量变成 4；2 号猪圈的第二个顾客是 3 号顾客，因此从 1 号顾客到 3 号顾 客有一条容量为∞的边；3 号猪圈的第一个顾客是 2 号顾客，所以从源点到 2 号 顾客有一条容量为 10 的边。

新的网络模型中最多只有 2 + N = 102 个结点，计算速度就可以相当快了。可 以这样理解这个新的网络模型：对于某一个顾客，如果他打开了猪圈 h，则在他 走后，他打开的所有猪圈里剩下的猪都有可能被换到 h 中，因而这些猪都有可能 被 h 的下一个顾客买走。所以对于一个顾客打开的所有猪圈，从该顾客到各猪圈 的下一个顾客，都要连一条容量为∞的边。

在面对网络流问题时，如果一时想不出很好的构图方法，不如先构造一个最 直观，或者说最“硬来”的模型，然后再用合并结点和边的方法来简化这个模 型。经过简化以后，好的构图思路自然就会涌现出来了。这是解决网络流问题 的一个好方法。

代码区

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e6 + ;
const int Max = 1e5 + ;

struct Edge
{
    int to, next;
    int flow;
}edge[Max];

int n, m, s, t;
int val[Max];                //每个猪舍的猪的个数
int last[Max];                //记录上一个打开这个猪舍的人
int head[Max], tot;
int dis[Max];

void init()
{
    memset(head, -, sizeof(head));tot = ;
    memset(last, -, sizeof(last));
    s = ;t = n + ;
}

void add(int u, int v, int flow)
{
    edge[tot].to = v;
    edge[tot].flow = flow;
    edge[tot].next = head[u];
    head[u] = tot++;
}

bool bfs()            //判断连通性，将图分层次
{
    queue<int>q;
    memset(dis, -, sizeof(dis));
    dis[s] = ;
    q.push(s);        //源点
    while (!q.empty())
    {
        int u = q.front();q.pop();

        for (int i = head[u]; i != -; i = edge[i].next)
        {
            int v = edge[i].to;
            if (dis[v] == - && edge[i].flow > )
            {
                dis[v] = dis[u] + ;
                q.push(v);
                if (v == t) return true;
            }
        }
    }
    return false;
}

int dfs(int u, int flow_in)
{
    if (u == t) return flow_in;
    int flow_out = ;            //实际流出流量
    for (int i = head[u];i != -;i = edge[i].next)
    {
        int v = edge[i].to;
        if (dis[v] == dis[u] +  && edge[i].flow > )
        {
            int flow_part = dfs(v, min(flow_in, edge[i].flow));
            if (flow_part == )continue;    //无法形成增广路
            flow_in -= flow_part;
            flow_out += flow_part;
            edge[i].flow -= flow_part;
            edge[i ^ ].flow += flow_part;
            if (flow_in == )break;
        }
    }
    return flow_out;
}

int max_flow()
{
    int sum = ;
    while (bfs())
    {
        sum += dfs(s, inf);
    }
    return sum;
}

int main()
{
#ifdef LOCAL
    //freopen("input.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
#endif
    while (scanf("%d%d", &m, &n) != EOF)
    {
        init();
        for (int i = ;i <= m;i++)
            scanf("%d", val + i);
        for (int i = , num, need;i <= n;i++)
        {
            scanf("%d", &num);
            int ans = ;                //记录从源点到这一结点的总流量
            for (int j = , x;j <= num;j++)
            {
                scanf("%d", &x);
                if (last[x] == -)
                {
                    ans += val[x];        //这个猪圈的第一个顾客
                }
                else                    //已经出现了，由前一次出现的位置向后建边
                {
                    add(last[x], i, inf);add(i, last[x], );
                }
                last[x] = i;
            }
            scanf("%d", &need);
            add(s, i, ans);add(i, s, );
            add(i, t, need);add(t, i, );
        }
        printf("%d\n", max_flow());
    }
    return ;
}