《数据结构与算法之美》 <06>栈：如何实现浏览器的前进和后退功能？

浏览器的前进、后退功能，我想你肯定很熟悉吧？

当你依次访问完一串页面 a-b-c 之后，点击浏览器的后退按钮，就可以查看之前浏览过的页面 b 和 a。当你后退到页面 a，点击前进按钮，就可以重新查看页面 b 和 c。但是，如果你后退到页面 b 后，点击了新的页面 d，那就无法再通过前进、后退功能查看页面 c 了。

假设你是 Chrome 浏览器的开发工程师，你会如何实现这个功能呢？

这就要用到我们今天要讲的“栈”这种数据结构。带着这个问题，我们来学习今天的内容。

如何理解“栈”？

关于“栈”，我有一个非常贴切的例子，就是一摞叠在一起的盘子。我们平时放盘子的时候，都是从下往上一个一个放；取的时候，我们也是从上往下一个一个地依次取，不能从中间任意抽出。后进者先出，先进者后出，这就是典型的“栈”结构。

从栈的操作特性上来看，栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。

我第一次接触这种数据结构的时候，就对它存在的意义产生了很大的疑惑。因为我觉得，相比数组和链表，栈带给我的只有限制，并没有任何优势。那我直接使用数组或者链表不就好了吗？为什么还要用这个“操作受限”的“栈”呢？

事实上，从功能上来说，数组或链表确实可以替代栈，但你要知道，特定的数据结构是对特定场景的抽象，而且，数组或链表暴露了太多的操作接口，操作上的确灵活自由，但使用时就比较不可控，自然也就更容易出错。

当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，我们就应该首选“栈”这种数据结构。

如何实现一个“栈”？

从刚才栈的定义里，我们可以看出，栈主要包含两个操作，入栈和出栈，也就是在栈顶插入一个数据和从栈顶删除一个数据。理解了栈的定义之后，我们来看一看如何用代码实现一个栈。

实际上，栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。

这里实现一个基于数组的顺序栈。基于链表实现的链式栈的代码，你可以自己试着写一下。

这段代码是用 Java 来实现的，但是不涉及任何高级语法，并且还用中文做了详细的注释，所以应该是可以看懂的。

// 基于数组实现的顺序栈
public class ArrayStack {
  private String[] items;  // 数组
  private int count;       // 栈中元素个数
  private int n;           //栈的大小

  // 初始化数组，申请一个大小为n的数组空间
  public ArrayStack(int n) {
    this.items = new String[n];
    this.n = n;
    this.count = 0;
  }

  // 入栈操作
  public boolean push(String item) {
    // 数组空间不够了，直接返回false，入栈失败。
    if (count == n) return false;
    // 将item放到下标为count的位置，并且count加一
    items[count] = item;
    ++count;
    return true;
  }

  // 出栈操作
  public String pop() {
    // 栈为空，则直接返回null
    if (count == 0) return null;
    // 返回下标为count-1的数组元素，并且栈中元素个数count减一
    String tmp = items[count-1];
    --count;
    return tmp;
  }
}

了解了定义和基本操作，那它的操作的时间、空间复杂度是多少呢？

不管是顺序栈还是链式栈，我们存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。

注意，这里存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n)。因为，这 n 个空间是必须的，无法省掉。所以我们说空间复杂度的时候，是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。

空间复杂度分析是不是很简单？时间复杂度也不难。不管是顺序栈还是链式栈，入栈、出栈只涉及栈顶个别数据的操作，所以时间复杂度都是 O(1)。

支持动态扩容的顺序栈

刚才那个基于数组实现的栈，是一个固定大小的栈，也就是说，在初始化栈时需要事先指定栈的大小。当栈满之后，就无法再往栈里添加数据了。尽管链式栈的大小不受限，但要存储 next 指针，内存消耗相对较多。那我们如何基于数组实现一个可以支持动态扩容的栈呢？

你还记得，我们在数组那一节，是如何来实现一个支持动态扩容的数组的吗？当数组空间不够时，我们就重新申请一块更大的内存，将原来数组中数据统统拷贝过去。这样就实现了一个支持动态扩容的数组。

所以，如果要实现一个支持动态扩容的栈，我们只需要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后，我们就申请一个更大的数组，将原来的数据搬移到新数组中。我画了一张图，你可以对照着理解一下。

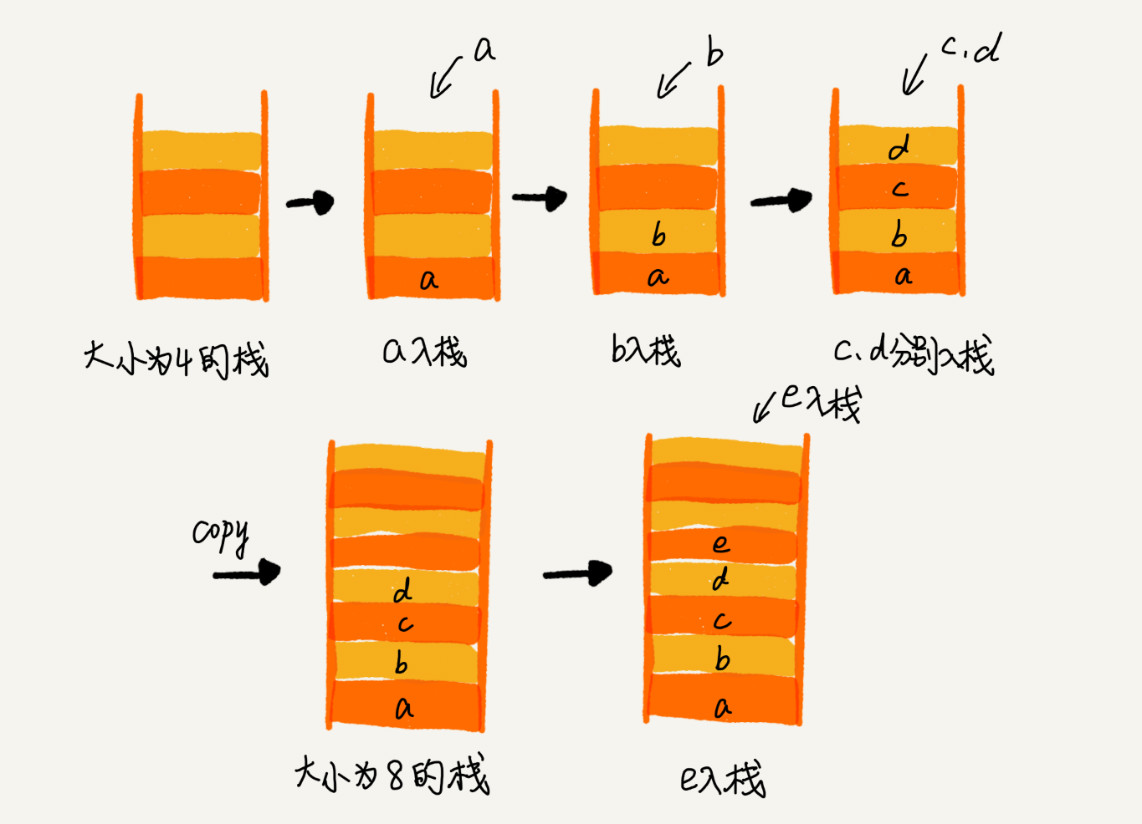
实际上，支持动态扩容的顺序栈，我们平时开发中并不常用到。我讲这一块的目的，主要还是希望带你练习一下前面讲的复杂度分析方法。所以这一小节的重点是复杂度分析。

你不用死记硬背入栈、出栈的时间复杂度，你需要掌握的是分析方法。能够自己分析才算是真正掌握了。现在我就带你分析一下支持动态扩容的顺序栈的入栈、出栈操作的时间复杂度。

对于出栈操作来说，我们不会涉及内存的重新申请和数据的搬移，所以出栈的时间复杂度仍然是 O(1)。但是，对于入栈操作来说，情况就不一样了。当栈中有空闲空间时，入栈操作的时间复杂度为 O(1)。但当空间不够时，就需要重新申请内存和数据搬移，所以时间复杂度就变成了 O(n)。

为了分析的方便，我们需要事先做一些假设和定义：

1. 栈空间不够时，我们重新申请一个是原来大小两倍的数组；

2. 为了简化分析，假设只有入栈操作没有出栈操作；

3. 定义不涉及内存搬移的入栈操作为 simple-push 操作，时间复杂度为 O(1)。

如果当前栈大小为 K，并且已满，当再有新的数据要入栈时，就需要重新申请 2 倍大小的内存，并且做 K 个数据的搬移操作，然后再入栈。但是，接下来的 K-1 次入栈操作，我们都不需要再重新申请内存和搬移数据，所以这 K-1 次入栈操作都只需要一个 simple-push 操作就可以完成。为了让你更加直观地理解这个过程，我画了一张图。

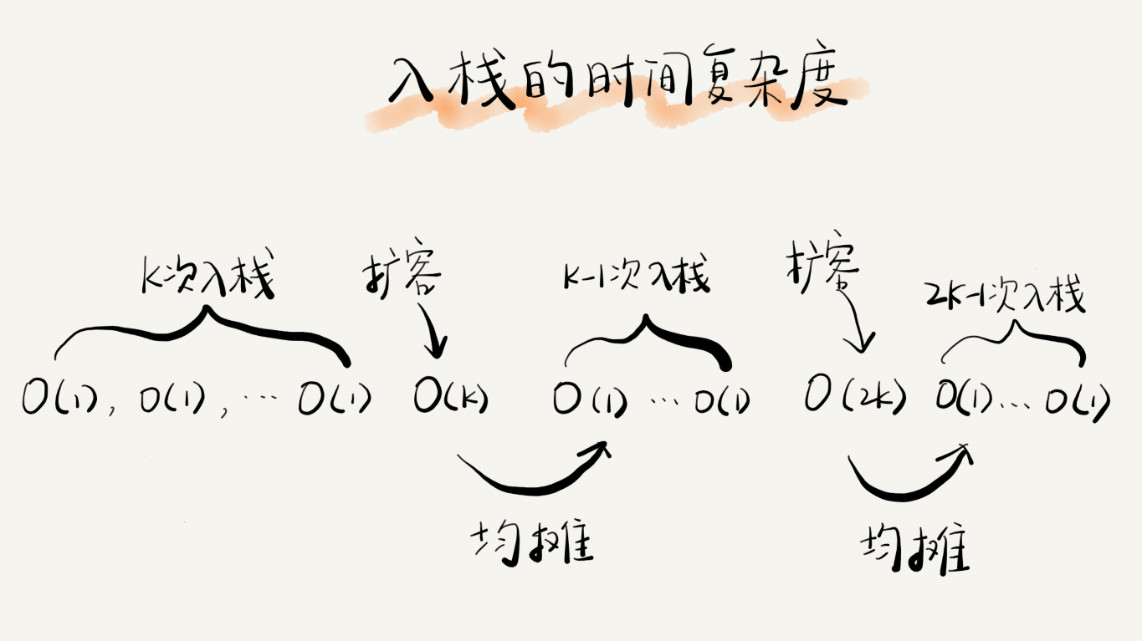
你应该可以看出来，这 K 次入栈操作，总共涉及了 K 个数据的搬移，以及 K 次 simple-push 操作。将 K 个数据搬移均摊到 K 次入栈操作，那每个入栈操作只需要一个数据搬移和一个 simple-push 操作。以此类推，入栈操作的均摊时间复杂度就为 O(1)。

通过这个例子的实战分析，也印证了前面讲到的，均摊时间复杂度一般都等于最好情况时间复杂度。因为在大部分情况下，入栈操作的时间复杂度 O 都是 O(1)，只有在个别时刻才会退化为 O(n)，所以把耗时多的入栈操作的时间均摊到其他入栈操作上，平均情况下的耗时就接近 O(1)。

栈在函数调用中的应用

前面我讲的都比较偏理论，我们现在来看下，栈在软件工程中的实际应用。栈作为一个比较基础的数据结构，应用场景还是蛮多的。其中，比较经典的一个应用场景就是函数调用栈。

我们知道，操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。为了让你更好地理解，我们一块来看下这段代码的执行过程。

int main() {
   int a = 1;
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

从代码中我们可以看出，main() 函数调用了 add() 函数，获取计算结果，并且与临时变量 a 相加，最后打印 res 的值。为了让你清晰地看到这个过程对应的函数栈里出栈、入栈的操作，我画了一张图。图中显示的是，在执行到 add() 函数时，函数调用栈的情况。

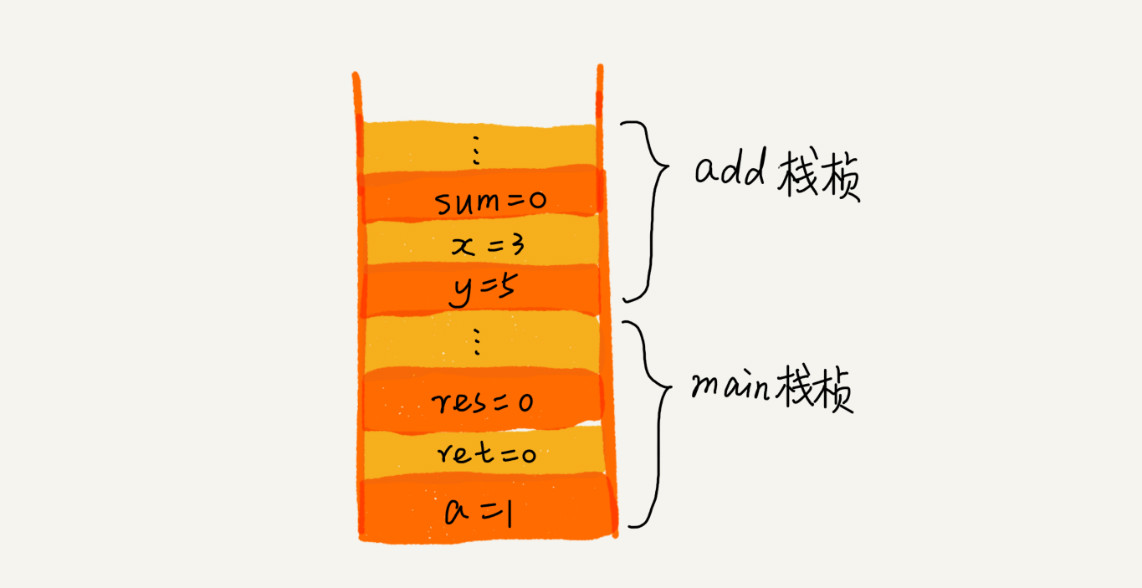
栈在表达式求值中的应用

我们再来看栈的另一个常见的应用场景，编译器如何利用栈来实现表达式求值。

为了方便解释，我将算术表达式简化为只包含加减乘除四则运算，比如：34+13*9+44-12/3。对于这个四则运算，我们人脑可以很快求解出答案，但是对于计算机来说，理解这个表达式本身就是个挺难的事儿。如果换作你，让你来实现这样一个表达式求值的功能，你会怎么做呢？

实际上，编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。我们从左向右遍历表达式，当遇到数字，我们就直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素进行比较。

如果比运算符栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取 2 个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

我将 3+5*8-6 这个表达式的计算过程画成了一张图，你可以结合图来理解我刚讲的计算过程。

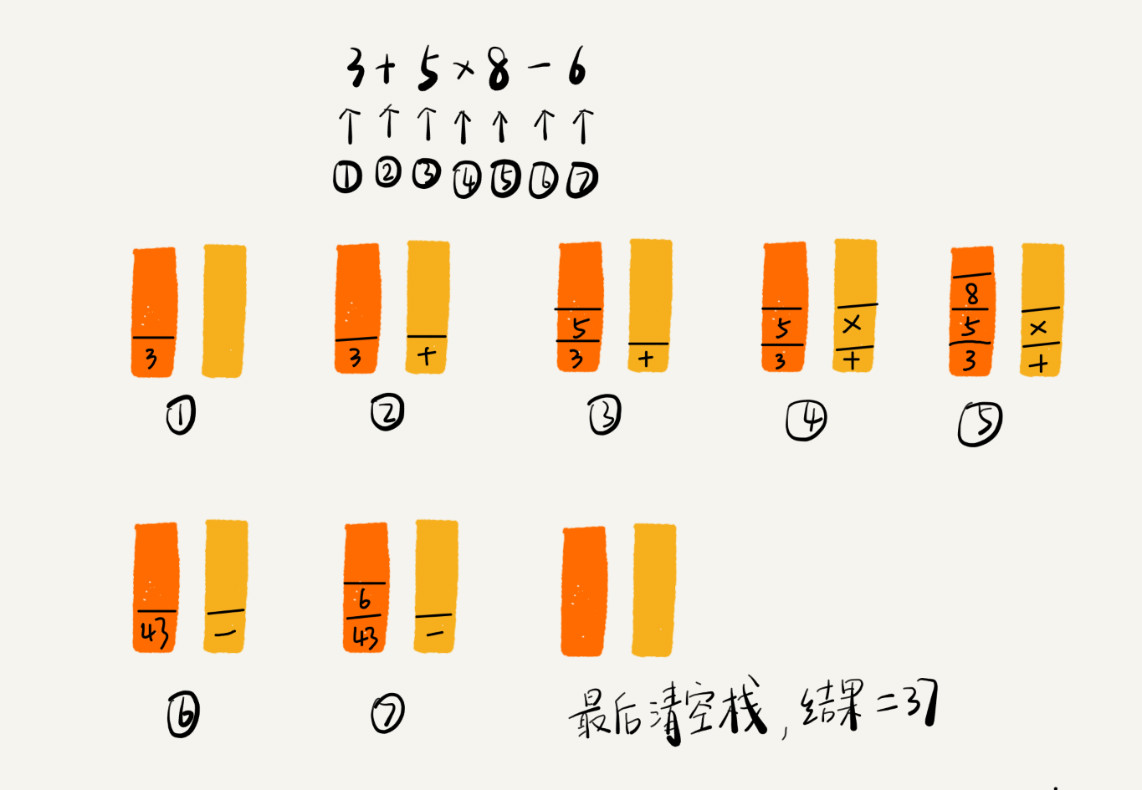
这样用两个栈来解决的思路是不是非常巧妙？你有没有想到呢？

栈在括号匹配中的应用

除了用栈来实现表达式求值，我们还可以借助栈来检查表达式中的括号是否匹配。

我们同样简化一下背景。我们假设表达式中只包含三种括号，圆括号 ()、方括号 [] 和花括号{}，并且它们可以任意嵌套。比如，{[] ()[{}]}或 [{()}([])] 等都为合法格式，而{[}()] 或 [({)] 为不合法的格式。那我现在给你一个包含三种括号的表达式字符串，如何检查它是否合法呢？

这里也可以用栈来解决。我们用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中；当扫描到右括号时，从栈顶取出一个左括号。如果能够匹配，比如“(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配，则继续扫描剩下的字符串。如果扫描的过程中，遇到不能配对的右括号，或者栈中没有数据，则说明为非法格式。

当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法格式；否则，说明有未匹配的左括号，为非法格式。

解答开篇

好了，我想现在你已经完全理解了栈的概念。我们再回来看看开篇的思考题，如何实现浏览器的前进、后退功能？其实，用两个栈就可以非常完美地解决这个问题。

我们使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈 X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。

比如你顺序查看了 a，b，c 三个页面，我们就依次把 a，b，c 压入栈，这个时候，两个栈的数据就是这个样子：

当你通过浏览器的后退按钮，从页面 c 后退到页面 a 之后，我们就依次把 c 和 b 从栈 X 中弹出，并且依次放入到栈 Y。这个时候，两个栈的数据就是这个样子：

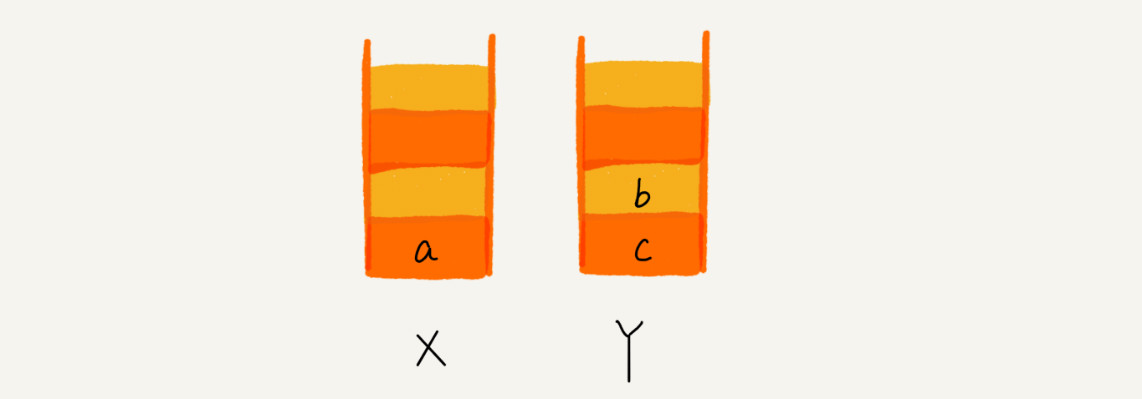
这个时候你又想看页面 b，于是你又点击前进按钮回到 b 页面，我们就把 b 再从栈 Y 中出栈，放入栈 X 中。此时两个栈的数据是这个样子：

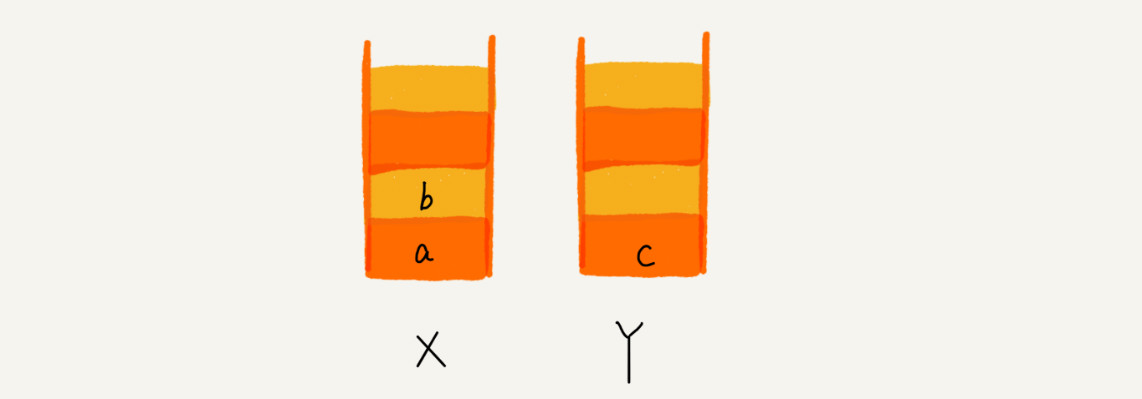
这个时候，你通过页面 b 又跳转到新的页面 d 了，页面 c 就无法再通过前进、后退按钮重复查看了，所以需要清空栈 Y。此时两个栈的数据这个样子：

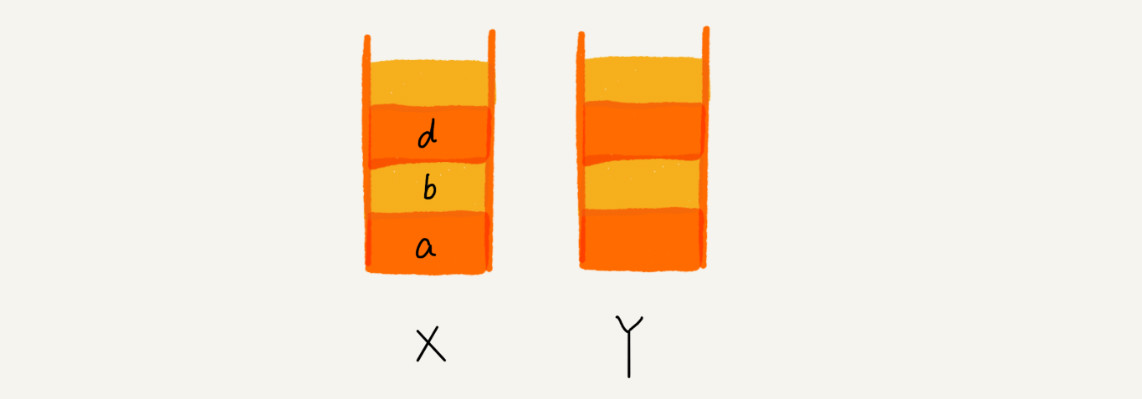
内容小结

我们来回顾一下今天讲的内容。栈是一种操作受限的数据结构，只支持入栈和出栈操作。后进先出是它最大的特点。栈既可以通过数组实现，也可以通过链表来实现。不管基于数组还是链表，入栈、出栈的时间复杂度都为 O(1)。除此之外，我们还讲了一种支持动态扩容的顺序栈，你需要重点掌握它的均摊时间复杂度分析方法。

资源地址： 点此进入

注： 本文出自极客时间（数据结构与算法之美），请大家多多支持王争老师。如有侵权，请及时告知。