动态查找之二叉树查找 c++实现

算法思想

二叉搜索树（又称二叉查找树或二叉排序树）BST树

二叉查找树

　　二叉查找树，也称二叉搜索树，或二叉排序树。其定义也比较简单，要么是一颗空树，要么就是具有如下性质的二叉树：

（1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2） 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3） 任意节点的左、右子树也分别为二叉查找树；

（4） 没有键值相等的节点。

二叉查找树的性质总结：　

a.二叉查找树还有一个性质，即对二叉查找树进行中序遍历，即可得到有序的数列。

​b.二叉查找树的查询复杂度，和二分查找一样，插入和查找的时间复杂度均为 O(logn) ，但是在最坏的情况下仍然会有 O(n) 的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡。

具体实现:

 /****
 * BinarySortTree.
 *
 ****/
 #include"stdafx.h"
 #include <iostream>
 #include<queue>
 using namespace std;
 typedef struct node
 {
     int elem;
     struct node* leftchild;
     struct node* rightchild;
 }BitNode,*BinTree;
 //insert binary tree function
 BinTree Insert_BinaryTree(BinTree &bt,int key)
 {
     if (bt == )
     {
         bt = new BitNode;
         bt->elem = key;
         bt->leftchild = ;
         bt->rightchild = ;
         return bt;
     }
     if (key < bt->elem)
     {
         bt->leftchild = Insert_BinaryTree(bt->leftchild,key);
     }
     else
     {
         bt->rightchild = Insert_BinaryTree(bt->rightchild, key);
     }
     return bt;
 }
 //for one search binary tree function
 int Search_BinaryTree(BinTree &bt,int key)
 {
     if (bt == ) return ;
     if (bt->elem == key) return ;

     if (key < bt->elem)
     {
         return Search_BinaryTree(bt->leftchild,key);
     }
     else
     {
         return Search_BinaryTree(bt->rightchild, key);
     }
 }
 // for another one search binary tree function
 int Search_BinaryTree(BinTree &bt, int key, BitNode ** p, BitNode** pf)
 {
     *p = bt;
     *pf = ;
     while (*p != )
     {
         if ((*p)->elem == key)
             return ;
         if ((*p)->elem > key)
         {
             *pf =*p;
             *p = (*p)->leftchild;
         }
         else
         {
             *pf = *p;
             *p = (*p)->rightchild;
         }
     }
     return ;
 }
 //delete binary tree function
 int Delete_BinaryTree(BinTree *bt,int key)
 {
     BitNode *p=*bt;
     BitNode *pf=;
     int findflag;
     if (bt == ) return ;
     findflag = Search_BinaryTree(*bt,key,&p,&pf);
     if (findflag == ) return ;
 //删除的节点是叶子节点
     if (p->leftchild ==  && p->rightchild == )
     {
         if (pf == )
         {
             delete bt;
             bt = ;
             return ;
         }
         if (p == pf->leftchild)
         {
             pf->leftchild = ;
             delete p;
             p = ;
             return ;
         }
         else
         {
             pf->rightchild = ;
             delete p;
             p = ;
             return ;
         }
     }
     //删除的节点只有一个子节点
     if (p->leftchild == )
     {
         if (pf = )
         {
             *bt = p->rightchild;
             delete p;
             return ;
         }
         if(p==pf->leftchild)
         {
             pf->leftchild = p->rightchild;
             delete p;
             return ;
         }
         else
         {
             pf->rightchild = p->rightchild;
             delete p;
             return ;
         }
     }

     if (p->rightchild == )
     {
         if (p == pf->leftchild)
         {
             pf->leftchild = p->leftchild;
             delete p;
             return ;
         }
         if (p == pf->rightchild)
         {
             pf->rightchild = p->leftchild;
             delete p;
             return ;
         }
     }
     //3.删除的节点含有两个子节点
     BitNode * prf = p;
     BitNode * pr = p->rightchild;
     while (pr->leftchild != )
     {
         prf = pr;
         pr = pr->leftchild;
     }
     if(prf == p)
     {
         p->elem = pr->elem;
         prf->rightchild = pr->rightchild;
     }
     else
     {
         p->elem = pr->elem;
         prf->leftchild = pr->rightchild;
     }
     delete pr;
     return ;

 }

 //print binary tree function
 void printTree(BitNode * bt)
 {
     queue<BitNode*> q;
     q.push(bt);
     while (!q.empty())
     {
         BitNode* p = q.front(); q.pop();
         if (p)
         {
             cout << p->elem << "->";
             q.push(p->leftchild);
             q.push(p->rightchild);
         }
     }
     cout << endl;
 }
 //test  function
 int main()
 {
     int a[] = { , , , , , , , , , };

     // initialization and creat the Binary Sort Tree.
     BinTree bt = ;
     for (int i = ; i < ; i++)
     {
         bt = Insert_BinaryTree(bt, a[i]);
     }
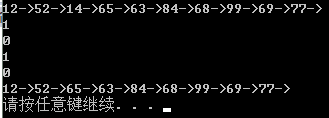
     printTree(bt);
     //search start.
     cout << Search_BinaryTree(bt, ) << endl;
     cout << Search_BinaryTree(bt, ) << endl;

     //delete start.
     cout << Delete_BinaryTree(&bt, ) << endl;

     //search 14 again.
     cout << Search_BinaryTree(bt, ) << endl;
     printTree(bt);
     system("pause");
     return ;
 }