机器学习算法的调试---梯度检验（Gradient Checking）

　　梯度检验是一种对求导结果进行数值检验的方法，该方法可以验证求导代码是否正确。

1. 数学原理

 　　考虑我们想要最小化以 θ 为自变量的目标函数 J(θ)（θ 可以为标量和可以为矢量，在 Numpy 的编程环境下，处理是一样的），迭代梯度更新公式为：

可以以sigmoid函数为例，

其导数形式为

我们可以实现梯度下降算法，那我们怎么知道g(z)梯度的准确性呢？

回忆导数的数学定义：

由此我们可得梯度校验的数值校验公式：

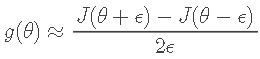
这便是梯度检验的原理。在实际应用中，我们常将ϵ设置为一个很小的常数，比如10^-4数量级，不会将它设的太小，比如10^-20，因为那将导致数值舍入误差。事实上，上式两端值的接近程度取决于 J 的具体形式，但在假定 ϵ=10⁻⁴ 的情况 下，通常会发现左右两端至少有四位有效数字是一致的（或者说精度至少在0.0001一级）。

2. 编程实现

import numpy as np

def sigmoid(z):
    return 1./(1+np.exp(-z))
def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))
def check_gradient(f, x0, epsilon):
    return (f(x0+epsilon) - f(x0-epsilon))/2/epsilon

if __name__ == '__main__':
    x0 = np.array([1, 2, 3])
    epsilon = 1e-4
    print(sigmoid_prime(x0))
            # [ 0.19661193  0.10499359  0.04517666]
    print(check_gradient(sigmoid, x0, epsilon))
            # [ 0.19661193  0.10499359  0.04517666]

　　

参考文献：

【1】机器学习算法的调试 —— 梯度检验（Gradient Checking）