八大排序算法之七—堆排序（Heap Sort）

堆排序是一种树形选择排序，是对直接选择排序的有效改进。

基本思想：

堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足

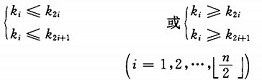
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。 若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

（a）大顶堆序列：（96, 83,27,38,11,09)

(b)  小顶堆序列：（12，36，24，85，47，30，53，91）

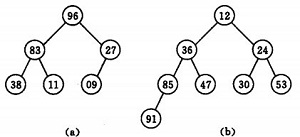
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。

因此，实现堆排序需解决两个问题： 1. 如何将n 个待排序的数建成堆； 2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。

首先讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。 调整小顶堆的方法：

1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。

2）将根结点与左、右子树中较小元素的进行交换。

3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法 （2）.

4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.

5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。

称这个自根结点到叶子结点的调整过程为筛选。如图：

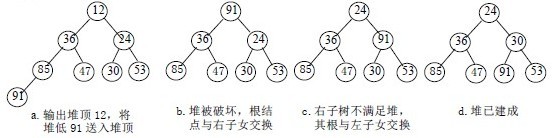
再讨论对n 个元素初始建堆的过程。 建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。

1）n 个结点的完全二叉树，则最后一个结点是第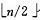个结点的子树。

2）筛选从第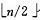个结点为根的子树开始，该子树成为堆。

3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。

如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）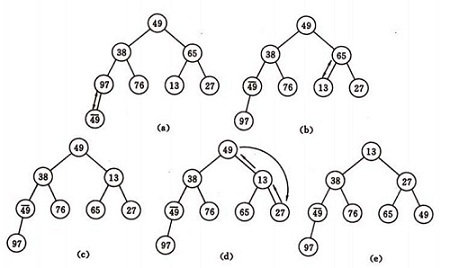                               

#include <iostream>

using namespace std;

void print(int a[],int n)
{
    for(int j=;j<n;j++)
        cout<<a[j]<<" ";
    cout<<endl;
}
void heapAdjust(int a[],int s,int length)
{
    int tmp=a[s];
    int child=*s+;//左孩子节点的位置
    while(child<length)
    {
        //如果存在右孩子，同时右孩子节点大于左孩子节点
        if(child+<length&&a[child]<a[child+])
            ++child;
        //如果较大孩子的节点大于父节点
        if(a[s]<a[child])
        {
            a[s]=a[child];
            s=child;
            child=*s+;
        }
        //孩子节点小于或等于父节点
        else
            break;

        //当时调整的节点放到比其大的孩子节点位置上
        a[s]=tmp;
    }
}
void buildingHeap(int a[],int length)
{
    //最后一个有孩子的节点的位置i=(length-1)/2
    for(int i=(length-)/;i>=;i--)
        heapAdjust(a,i,length);

}

/**
 * 堆排序算法
**/
void heapSort(int a[],int length)
{
    //初始化堆
    buildingHeap(a,length);
    //从最后一个元素开始对序列进行调整
    for(int i=length-;i>=;i--)
    {
        //交换堆顶元素s[0]和堆中最后一个元素
        int temp=a[i];
        a[i]=a[];
        a[]=temp;
        //每次交换堆顶元素和堆中最后一个元素之后，都要对堆进行调整
        heapAdjust(a,,i);
    }
}
int main()
{
    int a[]={,,,,,,,,,,,};
    int len=sizeof(a)/sizeof(int);
    print(a,len);
    heapSort(a,len);
    print(a,len);
    return ;
}