树和二叉树->遍历
文字描述
二叉树的先根遍历
若二叉树为空,则空操纵,否则
(1) 访问根结点
(2) 先根遍历左子树
(3) 先根遍历右子树
二叉树的中根遍历
若二叉树为空,则空操纵,否则
(1) 中根遍历左子树
(2) 访问根结点
(3) 中根遍历右子树
二叉树的后根遍历
若二叉树为空,则空操纵,否则
(1) 后根遍历左子树
(2) 后根遍历右子树
(3) 访问根结点
二叉树的层序遍历
自上到下,自左到右的遍历
树的先根遍历
先访问树的根结点,然后依次先根遍历树的每颗子树。
树的后根遍历
先依次后根遍历每颗子树,然后访问根结点。
森林的先根遍历
若森林非空,则:
(1) 访问森林中第一颗树的根结点
(2) 先根遍历第一个树中根结点的子树森林
(3) 先根遍历除第一颗树之后剩余的树构成的森林。
森林的中根遍历
若森林非空,则:
(1) 中根遍历森林中每一颗树的根结点的子树森林。
(2) 访问第一颗树的根结点
(3) 中根遍历除去第一颗树之后剩余的树构成的森林。
二叉树遍历算法的实现
二叉树遍历算法有三种:先根遍历、中根遍历、后根遍历; 用函数递归的方法很好实现,但是也可以不用函数递归,改用借助栈的方法, 具体描述如下:
非递归形式的二叉树的先根遍历
对于任一结点P:
(1)访问结点P,并将P入栈
(2)判断结点P的左孩子是否为空; 2.1)若为空,则取栈顶结点并进行出站并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P; 2.2)若为非空, 则将P的左孩子置为当前的结点P
(3)直到P为NULL并且栈为空,则遍历结束
非递归形式的二叉树的中根遍历-方法1
对于任一结点P
(1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理
(2)若左孩子为空, 则取栈顶元素并进行出栈操纵, 访问该栈顶元素,然后将栈顶结点的右孩子置为当前的P
(3)直到P为NULL并且栈为空则遍历结束
非递归形式的二叉树的后根遍历
要保证根结点在左孩子和右孩子被访问之后才能访问,因此对任一结点P,先将其入栈.; 如果P不存在孩子结点, 或者其孩子结点都被访问过了,则可以直接访问它; 若非这两种情况, 则将P的右孩子和左孩子入栈; 这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问, 左孩子和右孩子都在根结点前面被访问
非递归形式的二叉树的层序遍历
对二叉树进行遍历的搜索路径除了上诉按先根、中根或后根外,还可以从上到下、从左至右按层次进行,这种遍历方法叫二叉树的层序遍历,可以借助队列实现:
(1) 初始时,根结点入队列
(2) 然后,while循环判断队列不为空时,弹出一个结点,访问它,并把它的所有孩子结点入队列
示意图


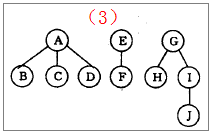
图(1)
二叉树的先根遍历 - + a * b – c d / e f
二叉树的中根遍历 a + b * c – d – e / f
二叉树的后根遍历 a b c d - * + e f / -
二叉树的层序遍历 - + / a * e f b - c d
图(2)
树的先根遍历 A B C D E
树的后根遍历 B D C E A
图(3)
森林的先根遍历 A B C D E F G H I J
森林的中根遍历 B C D A F E H J I G
算法分析
二叉树的遍历,无论哪种次序遍历,其时间复杂度均为n
所需辅助空间为便利过程中栈的最大深度,而最大深度为树的深度,即n
代码实现
#include <stdio.h>
#include <stdlib.h>
/*测试*/
#define DEBUG
/*
./a.out - + a \# \# \* b \# \# - c \# \# d \# \# / e \# \# f \# \#
*/
#define EQ(a, b) ((a)==(b))
/*树中结点的最大个数*/
#define MAX_TREE_SIZE 100 typedef char KeyType;
typedef int InfoType; /*树中的结点类型*/
typedef struct{
KeyType key;
InfoType otherinfo;
}TElemType; /*
* 二叉树的链式存储(二叉链表)
*
* 链表中的结点包含三个数据:数据域data,左指针域lchild,右指针域rchild
*/
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree; ///////////////////////////////////////////////////////////////////////////////////////////////////////
/////////////////////////////栈的相关结点定义和与非递归遍历算法相关的栈的函数声明-start////////////////
//栈的存储空间初始分配量
#define STACK_INIT_SIZE 100
//栈的存储空间分配增量
#define STACK_INCREMENT 10
//栈的结构体表示
typedef struct{
//栈底指针
BiTNode *base;
/*栈顶指针top;插入新元素时,top增1;删除栈顶元素时,top减1;
*非空栈中的栈顶指针始终在栈顶元素的下一个位置上。
*/
BiTNode *top;
//stacksize指示栈的当前可使用的最大容量
int stacksize;
}SqStack; /*构造一个空栈S*/
int InitStack(SqStack *S); /*若S为空栈,返回0,否则返回-1*/
int StackEmpty(SqStack *S); /*若S不为空,则用e返回S的栈顶元素,并返回0;否则返回-1*/
int GetTop(SqStack *S, BiTNode *e); /*插入元素e为新的栈顶元素*/
int Push(SqStack *S, BiTNode *e); /*若栈不为空,则删除S的栈顶元素,用e返回其值,返回0;否则返回-1*/
int Pop(SqStack *S, BiTNode *e);
///////////////////////////////////////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////////////////////////////////////// /*
* 按先根次序输入二叉树中结点的值,'#'表示空结点
* 构造二叉链表表示的二叉树T
*/
int I = ;
BiTree CreateBiTree(TElemType input[]){
TElemType data = input[I++];
BiTree T = NULL;
if(data.key == '#'){
T = NULL;
return T;
}else{
if(!(T=(BiTNode *)malloc(sizeof(BiTNode)))){
printf("Error: overflow!\n");
exit();
}
T->data = data;
T->lchild = CreateBiTree(input);
T->rchild = CreateBiTree(input);
return T;
}
} int vist(TElemType e){
printf("%c ", e.key);
return ;
} /*递归形式的二叉树的先根遍历算法*/
int PreOrderTraverse(BiTree T, int(*fun)(TElemType e)){
if(T){
fun(T->data);
PreOrderTraverse(T->lchild, fun);
PreOrderTraverse(T->rchild, fun);
return ;
}else{
return ;
}
} /*递归形式的二叉树的中根遍历算法*/
int InOrderTraverse(BiTree T, int (*fun)(TElemType e)){
if(T){
InOrderTraverse(T->lchild, fun);
fun(T->data);
InOrderTraverse(T->rchild, fun);
return ;
}else{
return ;
}
} /*递归形式的二叉树的后根遍历算法*/
int PostOrderTraverse(BiTree T, int (*fun)(TElemType e)){
if(T){
PostOrderTraverse(T->lchild, fun);
PostOrderTraverse(T->rchild, fun);
fun(T->data);
return ;
}else{
return ;
}
} /*
*非递归形式的二叉树的先根遍历
*
*对于任一结点P
*(1)访问结点P,并将P入栈
*(2)判断结点P的左孩子是否为空
* 2.1 若为空,则取栈顶结点并进行出站并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P
* 2.2 若为非空, 则将P的左孩子置为当前的结点P
*(3) 直到P为NULL并且栈为空,则遍历结束
*/
int PreOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){
SqStack S;
if(InitStack(&S)<){
return -;
}
BiTNode *p = T, q;
while(p || StackEmpty(&S)){
if(p){
fun(p->data);
Push(&S, p);
p = p->lchild;
}else{
Pop(&S, &q);
p = q.rchild;
}
}
} /*
*非递归形式的二叉树的中根遍历-方法1
*
*对于任一结点P
*(1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理
*(2)若左孩子为空, 则取栈顶元素并进行出栈操纵, 访问该栈顶元素,然后将栈顶结点的右孩子置为当前的P
*(3)直到P为NULL并且栈为空则遍历结束
*/
int InOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){
SqStack S;
if(InitStack(&S)<){
return -;
}
Push(&S, T);
BiTNode *p; while(StackEmpty(&S)<){
while((!GetTop(&S, p)) && p && !Push(&S, p->lchild));
Pop(&S, p);
fun(p->data);
if(StackEmpty(&S)){
Pop(&S, p);
fun(p->data);
Push(&S,p->rchild);
}
}
return ;
} /*非递归形式的二叉树的中根遍历-方法2*/
int InOrderTraverse_NonRecur2(BiTree T, int (*fun)(TElemType e)){
SqStack S;
if(InitStack(&S)<){
return -;
}
BiTNode *p = T, q;
while(p || StackEmpty(&S)){
if(p){
Push(&S, p);
p = p->lchild;
}else{
Pop(&S, &q);
fun(q.data);
p = q.rchild;
}
}
} /*比较两个结点是否相等,主要用于非递归后序遍历算法中判断两个结点是否为同一个结点*/
int compare(BiTNode *node1, BiTNode *node2)
{
if(node1 == NULL|| node2 == NULL){
return -;
}else if((node1->data.key == node2->data.key) && (node1->data.otherinfo == node2->data.otherinfo)){
return ;
}else{
return -;
}
} /*
*非递归形式的二叉树的后根遍历
*
*要保证根结点在左孩子和右孩子被访问之后才能访问,因此对任一结点P,先将其入栈.
*如果P不存在孩子结点, 或者其孩子结点都被访问过了,则可以直接访问它;
*若非这两种情况, 则将P的右孩子和左孩子入栈;
*这样就保证了每次取栈顶元素的时候,左孩子在右孩子前面被访问, 左孩子和右孩子都在根结点前面被访问
*/
int PostOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){
SqStack S;
if(InitStack(&S)<){
return -;
}
//当前结点
BiTNode *curr = (BiTNode*)malloc(sizeof(BiTNode));
//前一次被访问过的结点
BiTNode pre = {'', -}; Push(&S, T);
while(StackEmpty(&S)){
GetTop(&S, curr);
if((curr->lchild == NULL && curr->rchild == NULL)
|| (!compare(curr->lchild, &pre)|| !compare(curr->rchild, &pre))){
//如果当前结点没有孩子结点或者该结点的孩子结点都被访问过
fun(curr->data);
pre = *curr;
Pop(&S, curr);
}else{
//右孩子入栈
Push(&S, curr->rchild);
//左孩子入栈
Push(&S, curr->lchild);
}
} return ;
} int main(int argc, char *argv[])
{
if(argc < )
return -; TElemType input[MAX_TREE_SIZE];
int i = , j = ;
for(i=; i<MAX_TREE_SIZE; i++){
input[i].key = '#';
} //按先根次序输入二叉树中结点的值,'-'表示空树
for(i=; i<argc; i++){
if(i>MAX_TREE_SIZE)
break;
input[i-].key = argv[i][];
input[i-].otherinfo = i-;
}
#ifdef DEBUG
printf("按先根顺序建立二叉树(#表示空结点):\n");
for(j=; j< i-; j++){
printf("%c ", input[j].key);
}
printf("\n");
#endif
BiTree T = CreateBiTree(input); printf("递归形式的二叉树的先根遍历算法\n");
PreOrderTraverse(T, vist); printf("\n递归形式的二叉树的中根遍历算法\n");
InOrderTraverse(T, vist); printf("\n递归形式的二叉树的后根遍历算法\n");
PostOrderTraverse(T, vist); printf("\n非递归形式的二叉树的先根遍历\n");
PreOrderTraverse_NonRecur(T,vist); printf("\n非递归形式的二叉树的中根遍历-方法1\n");
InOrderTraverse_NonRecur(T,vist); printf("\n非递归形式的二叉树的中根遍历-方法2\n");
InOrderTraverse_NonRecur2(T,vist); printf("\n非递归形式的二叉树的后根遍历\n");
PostOrderTraverse_NonRecur(T,vist);
printf("\n");
return ;
} /////////////////////////////////////////////////////////////////////////////////////
/////////////////////////////与非递归遍历算法相关的栈的函数实现-start////////////////
/*构造一个空栈S*/
int InitStack(SqStack *S)
{
S->base = (BiTNode *)malloc(STACK_INIT_SIZE * sizeof(BiTNode));
if(!S->base){
return -;
}
S->top = S->base;
S->stacksize = STACK_INIT_SIZE;
return ;
} /*若S为空栈,返回0,否则返回-1*/
int StackEmpty(SqStack *S)
{
if(S->top == S->base){
return ;
}else{
return -;
}
} /*若S不为空,则用e返回S的栈顶元素,并返回0;否则返回-1*/
int GetTop(SqStack *S, BiTNode *e)
{
if(S->top == S->base){
return -;
}else{
if((S->top-) == NULL){
e = NULL;
}else{
*e = *(S->top-);
}
return ;
}
} /*插入元素e为新的栈顶元素*/
int Push(SqStack *S, BiTNode *e)
{
//栈满,需要追加存储空间
if((S->top-S->base) >= S->stacksize){
S->base = (BiTNode *)realloc(S->base, (S->stacksize+STACK_INCREMENT) * sizeof(BiTNode));
if(!S->base){
return -;
}
S->top = S->base + S->stacksize;
S->stacksize += STACK_INCREMENT;
}
if(e == NULL){
return -;
}else{
*S->top = *e;
}
S->top += ;
return ;
} /*若栈不为空,则删除S的栈顶元素,用e返回其值,返回0;否则返回-1*/
int Pop(SqStack *S, BiTNode *e)
{
if(S->top == S->base){
return -;
}else{
S->top -= ;
*e = *(S->top);
return ;
}
} /////////////////////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////////////////////
二叉树的遍历(递归和非递归)
#include <stdio.h>
#include <stdlib.h> #define DEBUG
#define EQ(a, b) ((a)==(b))
/*树中结点的最大个数*/
#define MAX_TREE_SIZE 100 typedef char KeyType;
typedef int InfoType; /*树中的结点类型*/
typedef struct{
KeyType key;
InfoType otherinfo;
}TElemType; /*
* 二叉树的链式存储(二叉链表)
*
* 链表中的结点包含三个数据:数据域data,左指针域lchild,右指针域rchild
*/
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree; ////////////////////////////////////////////////////////////////////////////////
//与队列相关的结构体和函数声明
typedef struct QNode{
BiTNode data;
struct QNode *next;
}QNode, *QuenePtr; typedef struct{
QuenePtr front;
QuenePtr rear;
}LinkQueue; LinkQueue* InitQueue(void);
int QueueEmpty(LinkQueue *Q);
int GetHead(LinkQueue *Q, BiTNode *e);
int EnQueue(LinkQueue *Q, BiTNode *e);
int DeQueue(LinkQueue *Q, BiTNode *e);
//////////////////////////////////////////////////////////////////////////////// /*
* 建立二叉链表
*
* 按先根次序输入二叉树中结点的值,'#'表示空结点
*/
int I = ;
BiTree CreateBiTree(TElemType input[]){
TElemType data = input[I++];
BiTree T = NULL;
if(data.key == '#'){
T = NULL;
return T;
}else{
if(!(T=(BiTNode *)malloc(sizeof(BiTNode)))){
printf("Error: overflow!\n");
exit();
}
T->data = data;
T->lchild = CreateBiTree(input);
T->rchild = CreateBiTree(input);
return T;
}
} int vist(TElemType e){
printf("%c ", e.key);
return ;
} /*
* 非递归形式的二叉树的层序遍历
*
* 从上到下,从左到右按层次遍历。
* (1) 初始时,根结点入队列
* (2) 然后,while循环判断队列不为空时,弹出一个结点,访问它,并把它的所有孩子结点入队列
*/
int LevelOrderTraverse_NonRecur(BiTree T, int (*fun)(TElemType e)){
LinkQueue *Q = InitQueue();
if(!Q){
return -;
}
EnQueue(Q, T);
BiTNode node;
while(QueueEmpty(Q)){
//删除最前面的结点
DeQueue(Q, &node);
fun(node.data);
//判断最前面的左孩子结点是否为空,不是就放入队列
if(node.lchild){
EnQueue(Q, node.lchild);
}
//判断最前面的右孩子结点是否为空,不是就放入队列
if(node.rchild){
EnQueue(Q, node.rchild);
}
}
return ;
} int main(int argc, char *argv[])
{
if(argc < )
return -;
TElemType input[MAX_TREE_SIZE];
int i = , j = ;
for(i=; i<MAX_TREE_SIZE; i++){
input[i].key = '#';
} //按先根次序输入二叉树中结点的值,'#'表示空树
for(i=; i<argc; i++){
if(i>MAX_TREE_SIZE)
break;
input[i-].key = argv[i][];
input[i-].otherinfo = i-;
}
#ifdef DEBUG
printf("按先根顺序建立二叉树(#表示空结点):\n");
for(j=; j< i-; j++){
printf("%c ", input[j].key);
}
printf("\n");
#endif
BiTree T = CreateBiTree(input);
printf("非递归形式的二叉树的层序遍历\n");
LevelOrderTraverse_NonRecur(T, vist);
printf("\n");
return ;
} ////////////////////////////////////////////////////////////////////////////////
//与队列相关的函数的实现
LinkQueue* InitQueue(void)
{
LinkQueue *Q = (LinkQueue*)malloc(sizeof(LinkQueue));
Q->front = Q->rear = (QuenePtr)malloc(sizeof(QNode));
if(!Q->front){
printf("malloc fail!\n");
return NULL;
}
return Q;
} int QueueEmpty(LinkQueue *Q)
{
if(Q->front == Q->rear){
return ;
}else{
return -;
}
} int GetHead(LinkQueue *Q, BiTNode *e)
{
if(Q->front == Q->rear){
return -;
}
*e = Q->front->next->data;
return ;
} int EnQueue(LinkQueue *Q, BiTNode *e)
{
QuenePtr p = (QuenePtr)malloc(sizeof(QNode));
if(!p){
printf("malloc fail!\n");
return -;
}
p->data = *e;
p->next = NULL;
Q->rear->next = p;
Q->rear = p;
return ;
} int DeQueue(LinkQueue *Q, BiTNode *e)
{
if(Q->front == Q->rear){
return -;
}
QuenePtr p = Q->front->next;
*e = p->data;
Q->front->next = p->next;
if(p == Q->rear){
Q->rear = Q->front;
}
free(p);
return ;
}
////////////////////////////////////////////////////////////////////////////////
二叉树的层序遍历
运行
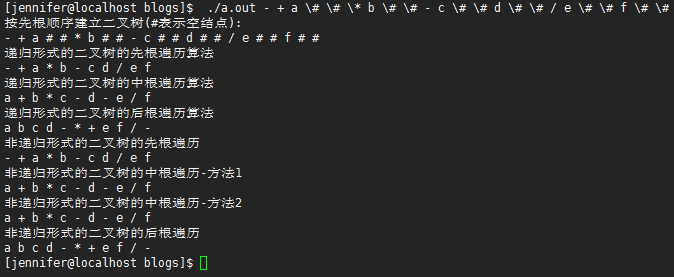

树和二叉树->遍历的更多相关文章
- hdu 4605 线段树与二叉树遍历
思路: 首先将所有的查询有一个vector保存起来.我们从1号点开始dfs这颗二叉树,用线段树记录到当前节点时,走左节点的有多少比要查询该节点的X值小的,有多少大的, 同样要记录走右节点的有多少比X小 ...
- UVa 10562看图写树(二叉树遍历)
https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- lintcode :前序遍历和中序遍历树构造二叉树
解题 前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: 2 / \ 1 3 注意 你可以假设树中不存 ...
- lintcode: 中序遍历和后序遍历树构造二叉树
题目 中序遍历和后序遍历树构造二叉树 根据中序遍历和后序遍历树构造二叉树 样例 给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2] 返回如下的树: 2 / \ 1 3 注意 你可 ...
- python数据结构之树和二叉树(先序遍历、中序遍历和后序遍历)
python数据结构之树和二叉树(先序遍历.中序遍历和后序遍历) 树 树是\(n\)(\(n\ge 0\))个结点的有限集.在任意一棵非空树中,有且只有一个根结点. 二叉树是有限个元素的集合,该集合或 ...
- python数据结构之树(二叉树的遍历)
树是数据结构中非常重要的一种,主要的用途是用来提高查找效率,对于要重复查找的情况效果更佳,如二叉排序树.FP-树. 本篇学习笔记来自:二叉树及其七种遍历方式.python遍历与非遍历方式实现二叉树 介 ...
- LintCode-72.中序遍历和后序遍历树构造二叉树
中序遍历和后序遍历树构造二叉树 根据中序遍历和后序遍历树构造二叉树 注意事项 你可以假设树中不存在相同数值的节点 样例 给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2] 返回如下的树: ...
- LintCode-73.前序遍历和中序遍历树构造二叉树
前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 注意事项 你可以假设树中不存在相同数值的节点 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: ...
- javascript实现数据结构: 树和二叉树的应用--最优二叉树(赫夫曼树),回溯法与树的遍历--求集合幂集及八皇后问题
赫夫曼树及其应用 赫夫曼(Huffman)树又称最优树,是一类带权路径长度最短的树,有着广泛的应用. 最优二叉树(Huffman树) 1 基本概念 ① 结点路径:从树中一个结点到另一个结点的之间的分支 ...
随机推荐
- Ubuntu python3 安装pip
python2:sudo apt-get install python-pip python3:sudo apt-get install python3-pip 切换python2和python3的版 ...
- Android开发(二十一)——自动更新
参考: [1] Android应用自动更新功能的代码实现.http://www.cnblogs.com/coolszy/archive/2012/04/27/2474279.html
- Weka算法Clusterers-Xmeans源代码分析(一)
<p></p><p><span style="font-size:18px">上几篇博客都是分析的分类器算法(有监督学习),这次就分 ...
- python风格的抽象工厂模式
抽象工厂模式: 提供一个接口,用户创建多个相关或依赖对象,而不需要指定具体类. 原则: 依赖抽象,不依赖具体类. 实例: 用不同原材料制作不同口味的披萨,创建不同原材料的工厂,不同实体店做出口味不同的 ...
- [原]openstack-kilo--issue(二十二) 虚拟机的vnc console图像调用错误
[问题点] 在打开node compute 上vm的vnc console窗口时候发现vm1-compute1调用的是vm1-controller上的vnc图像 =================== ...
- Dom捕捉事件和冒泡事件-原理与demo测试
先参考一下百度百科对冒泡事件流的解释: ----------不喜欢读文字的同学,可以直接看下面demo,传递顺序简单明了! http://baike.baidu.com/link?url=kaeJHT ...
- es7 class装饰器
文档http://es6.ruanyifeng.com/#docs/decorator ts文档 https://www.tslang.cn/docs/handbook/decorators.html ...
- c++中map按key和value排序
``` #include<iostream> #include<algorithm> #include<vector> #include<map> #i ...
- 170828、Eclipse Java注释模板设置详解以及版权声明
编辑注释模板的方法:Window->Preference->Java->Code Style->Code Template 然后展开Comments节点就是所有需设置注释的元素 ...
- Maven知识点积累二
①maven常用命令: mvn clean:清除target下编译生成的class文件 mvn compile:编译 mvn package:打包放到target下 mvn install:打包并放到 ...
