洛谷 - UVA11346 - 概率 Probability - 积分

要是没学过高等数学的积分怎么办呢？可以求助于自适应辛普森法。

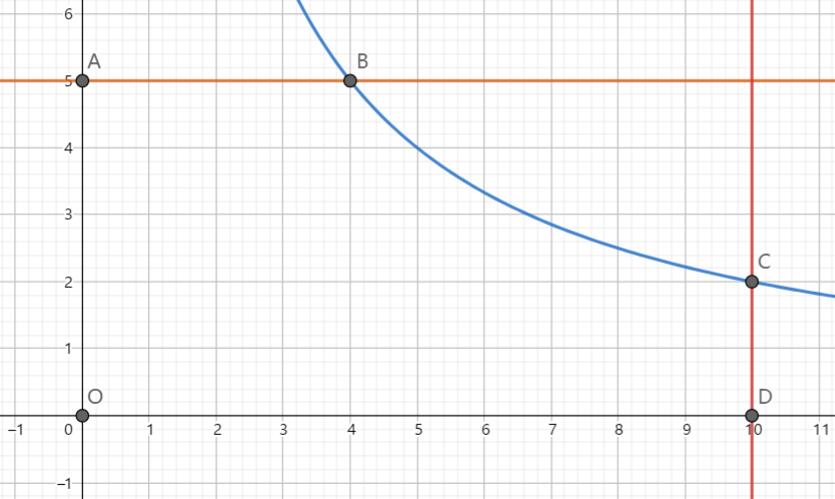
容易发现其实这个图形是对称的，我们只要求第一象限就可以了，第一象限如上图。

由于取点是在面积内等概率的，由高中的几何概型可知，所求概率为：

1.当S<=ab，则双曲线与矩形有交点，概率的分子为上图中 矩形面积 减去 OABCD面积，分母为矩形面积。

2.当S>ab，则概率为1。

所求的面积为双曲线 \(y=\frac{S}{x}\) 在 直线 \(y=b\) 下，从 \(0\) 到 \(a\) 的积分。

表述为 \(F(x)=min(\frac{S}{x},b)\) 。

然后我们套一个自适应辛普森法求积分就可以了。

（不可能是省选的难度，连我都会）

在F中有对无穷小的特判，去掉的话不会有什么问题，但是总感觉能避免除以0的RE挺好的。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

double seps=1e-12;
double a,b,S;

double F(double x) {
    //需要积分的函数F
    /*if(x<1e-8)
        return b;*/
    return min(b,S/x);
}

double simpson(double l,double r) {
    double mid=(l+r)/2;
    return (F(l)+4*F(mid)+F(r))*(r-l)/6;
}

double asr(double l,double r,double A) {
    double mid=(l+r)/2;
    double L=simpson(l,mid),R=simpson(mid,r);
    if(fabs(L+R-A)<=15*seps)
        return L+R+(L+R-A)/15.0;
    return asr(l,mid,L)+asr(mid,r,R);
}

double asr(double l,double r) {
    return asr(l,r,simpson(l,r));
}

int main() {
    int t;
    cin>>t;
    while(t--) {
        cin>>a>>b>>S;
        double p=0;
        if(S+(-1e-10)<=0)
            p=1.0;
        else if(S+(1e-10)>=a*b) {
            p=0.0;
        } else {
            p=1.0-asr(0,a)/(a*b);
        }
        p*=100.0;
        printf("%.6f%\n",p);
    }
}