*本文主要记录和分享学习到的知识，算不上原创。

*参考文献见链接。

旅行商问题、背包问题都是0-1规划问题中最为经典的问题。

通常来说，当我们学习并熟悉一种求解混合整数问题的技巧时，可以用这种技巧来求解旅行商问题或者背包问题，以此来验证自己对该技巧的掌握程度。

目录

　　什么是旅行商问题

　　旅行商问题的数学模型

什么是旅行商问题

定义

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?

时间复杂度

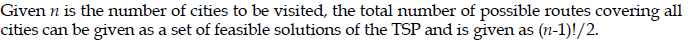
分类

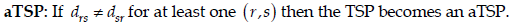
其中，sTSP是最简单的TSP问题。

旅行商问题的数学建模

Integer programming formulation of sTSP

变量

This formulation associates a binary variable xij with each edge (i, j), equal to 1 if and only if the edge appears in the optimal tour. The formulation of TSP is as follows.

模型

Integer programming formulation of aTSP

变量

xij is a binary variable, associated with arc (i,j) and equal to 1 if and only if the arc appears in the  optimal tour.

模型

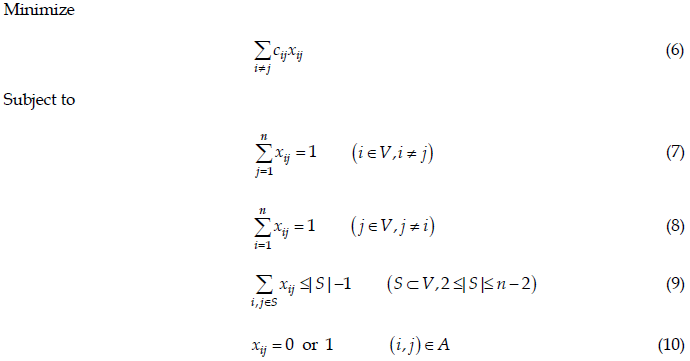
参考文献

https://en.wikipedia.org/wiki/Travelling_salesman_problem

Traveling Salesman Problem, Theory and Applications, Edited by Donald Davendra p. cm.ISBN 978-953-307-426-9

MIP经典问题：旅行商问题 (traveling salesman problem)的更多相关文章

  1. 旅行商问题（Traveling Salesman Problem,TSP)的+Leapms线性规划模型及c++调用

    知识点 旅行商问题的线性规划模型旅行商问题的+Leapms模型及CPLEX求解C++调用+Leapms 旅行商问题 旅行商问题是一个重要的NP-难问题.一个旅行商人目前在城市1,他必须对其余n-1个城 ...

  2. 【智能算法】用模拟退火(SA, Simulated Annealing)算法解决旅行商问题 (TSP, Traveling Salesman Problem)

    喜欢的话可以扫码关注我们的公众号哦,更多精彩尽在微信公众号[程序猿声] 文章声明 此文章部分资料和代码整合自网上,来源太多已经无法查明出处,如侵犯您的权利,请联系我删除. 01 什么是旅行商问题(TS ...

  3. Complexity and Tractability (3.44) - The Traveling Salesman Problem

    Copied From:http://csfieldguide.org.nz/en/curriculum-guides/ncea/level-3/complexity-tractability-TSP ...

  4. 多线程动态规划算法求解TSP(Traveling Salesman Problem) 并附C语言实现例程

    TSP问题描述: 旅行商问题,即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题.货郎担问题,是数学领域中著名问题之一.假设有一个旅行商人要拜访n个城市,他必须 ...

  5. TSP（Traveling Salesman Problem）-----浅谈旅行商问题（动态规划,回溯实现）

    1.什么是TSP问题 一个售货员必须访问n个城市,这n个城市是一个完全图,售货员需要恰好访问所有城市的一次,并且回到最终的城市. 城市于城市之间有一个旅行费用,售货员希望旅行费用之和最少. 完全图:完 ...

  6. Speeding Up The Traveling Salesman Using Dynamic Programming

    Copied From:https://medium.com/basecs/speeding-up-the-traveling-salesman-using-dynamic-programming-b ...

  7. PAT-1150（Travelling Salesman Problem）旅行商问题简化+模拟图+简单回路判断

    Travelling Salesman Problem PAT-1150 #include<iostream> #include<cstring> #include<st ...

  8. PAT A1150 Travelling Salesman Problem （25 分）——图的遍历

    The "travelling salesman problem" asks the following question: "Given a list of citie ...

  9. PAT 甲级 1150 Travelling Salesman Problem

    https://pintia.cn/problem-sets/994805342720868352/problems/1038430013544464384 The "travelling ...

随机推荐

  1. asp.net多文件上传

    文件上传简单实现是非常容易的,但是想要更高的要求,比如通过ajax上传文件.一次上传多个文件.文件比较大等等,这里面的坑就不是很容易填(对于新手来说).因此在这里我准备通过ajax实现多文件上传.在开 ...

  2. python入门之三元运算，存址方式，深浅拷贝

    三元运算 格式: name = 值1 if 条件 else 值2 如果条件为True,那么将值1赋值给name,条件为False,那么将值2赋值给name 存址方式 不同的数据类型在内存中的存址方式不 ...

  3. 记录一下filter

    filter是什么,如它的字面意思,就是拦截器.它可以在request到达相关资源之前,比如servlet之前先处理requeset,也可以拦截或处理从某个资源比如servlet发出的response ...

  4. compare `lvs/haproxy/nginx`

    特性 LVS Nginx Haproxy 工作层 四层(传输层TCP/UDP) 七层(应用层) 四层.七层 应用范围 基于TCP和UDP之上的协议都可以 Http.mail HTTP.TCP之上应用 ...

  5. css与JS知识整理

    CSS知识 CSS选择器:基础中的核心,选择器指明了{}中“样式”作用的对象,也就是“样式”作用于网页中的哪些元素. CSS选择器类型:一共三大类. 基础选择器    属性选择器    组合选择器  ...

  6. aspectj xml

    1.接口和类 1.1 ISomeService 接口 public interface ISomeService { public void doSome(); public void dade(); ...

  7. Spring源码：Spring IoC容器加载过程（2）

    Spring源码版本:4.3.23.RELEASE 一.加载XML配置 通过XML配置创建Spring,创建入口是使用org.springframework.context.support.Class ...

  8. Mysql order by 多字段排序

    mysql单个字段降序排序: select * from table order by id desc; mysql单个字段升序排序: select * from table order by id ...

  9. 登录界面点击登录后如何延迟提示成功的div的显示时间并跳转

    需求: 在登录页面点击sign in跳转到下个页面之前,我需要显示成功的窗口2秒然后自动关闭 那我们来研究下setTimeout: 关于这个setTimeout首先下面的代码实现的是两秒之后再显示Su ...

  10. fun下载内容批量收集

    1.download title and url #!/usr/bin/env python #-*- coding:utf-8 -*- import re, urllib2,threading de ...