luogu3231 [HNOI2013]消毒

前置技能：poj3041

---

如果是二维平面有一些方块，这些方块被染了黑色，你每次可以选择 \((x,y)\) 的区域染成白色，代价是 \(\min(x,y)\)，问你付出的最小代价



显然我们不会这么染



因为这样我们的代价是 \(\min(x,y)\)，为了研究的方便我们假设 \(x\) 比 \(y\) 小，那我们就相当于染 \(x\) 次 \(1 \times y\) 的区域，因此一次染一片总是不如一次染一条的。下面这么染就很好



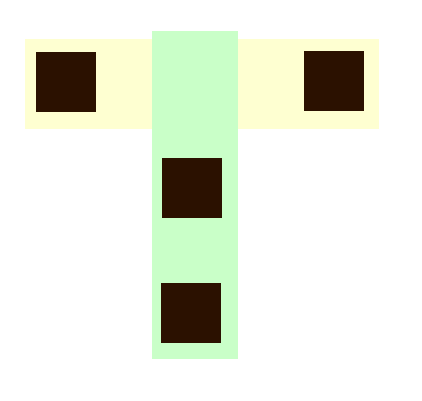
所以我们建立二分图，对于每个黑色块 \((x,y)\)，我们将其处于第一部的 \(x\) 与处于第二部的 \(y\) 连接，求一个最小点覆盖。二分图中最小点覆盖=最大匹配，就得到了答案。

---

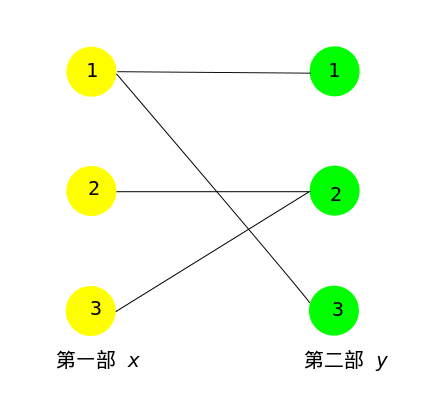
回到本题，题目中扩展到了三维空间，我们也有类似的想法。然而我们并不会三分图匹配这种东西……

观察到 \(abc \leq 5000\)，反证法可以轻易地证出 \(a,b,c\) 中有一个 \(\leq \sqrt[3]{5000} \approx 17.1\)，为了研究方便我们钦定是 \(a \leq \sqrt[3]{5000}\)，这样就暴力枚举 \(1\ldots a\) 中的某一层是直接削掉还是一会儿再处理（只有这两种情况，别的都不好，想一想为什么）。

对于没有被直接削掉的层，我们把它们剥离出来，然后拍扁成二维平面上的问题求解。

---

代码。跑得不是很快，借鉴了一下网上的代码

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int T, hea[5005], cnt, a, b, c, minn, sx[4][5005], uu, ans, lnk[5005], qaq;
bool isn[5005], qwq[25], vis[5005];
struct Edge{
	int too, nxt;
}edge[5005];
void add_edge(int fro, int too){
	edge[++cnt].nxt = hea[fro];
	edge[cnt].too = too;
	hea[fro] = cnt;
}
bool dfs(int x){
	for(int i=hea[x]; i; i=edge[i].nxt){
		int t=edge[i].too;
		if(!vis[t]){
			vis[t] = true;
			if(!lnk[t] || dfs(lnk[t])){
				lnk[t] = x;
				return true;
			}
		}
	}
	return false;
}
void work(int x){
	for(int i=1; i<=b; i++)	hea[i] = 0;
	cnt = 0;
	for(int i=1; i<=c; i++)	lnk[i] = 0;
	int tmp=0;
	for(int i=0; i<a; i++){
		if(x&(1<<i))	qwq[i+1] = false, tmp++;
		else	qwq[i+1] = true;
	}
	for(int i=1; i<=qaq; i++)
		if(qwq[sx[1][i]])
			add_edge(sx[2][i], sx[3][i]);
	for(int i=1; i<=b; i++){
		for(int j=1; j<=c; j++)	vis[j] = false;
		if(dfs(i))	tmp++;
	}
	ans = min(tmp, ans);
}
int main(){
	cin>>T;
	while(T--){
		qaq = 0;
		ans = 0x3f3f3f3f;
		scanf("%d %d %d", &a, &b, &c);
		minn = min(a, min(b, c));
		for(int i=1; i<=a; i++)
			for(int j=1; j<=b; j++)
				for(int k=1; k<=c; k++){
					scanf("%d", &uu);
					if(!uu)	continue;
					sx[1][++qaq] = i;
					sx[2][qaq] = j;
					sx[3][qaq] = k;
				}
		if(minn==b)	swap(a, b), swap(sx[1], sx[2]);
		else if(minn==c)	swap(a, c), swap(sx[1], sx[3]);
		for(int i=0; i<(1<<a); i++)
			work(i);
		printf("%d\n", ans);
	}
	return 0;
}