[CQOI2018] 社交网络

题目背景

当今社会，在社交网络上看朋友的消息已经成为许多人生活的一部分。通常，一个用户在社交网络上发布一条消息(例如微博、状态、Tweet等) 后，他的好友们也可以看见这条消息，并可能转发。转发的消息还可以继续被人转发，进而扩散到整个社交网络中。

题目描述

在一个实验性的小规模社交网络中我们发现，有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程，我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便，我们将初始消息发送者编号为1,其他用户编号依次递增。

该社交网络上的所有好友关系是已知的,也就是说对于A、B 两个用户，我们知道A 用户可以看到B 用户发送的消息。注意可能存在单向的好友关系，即lA 能看到B 的消息，但B 不能看到A 的消息。

还有一个假设是，如果某用户看到他的多个好友转发了同一条消息，他只会选择从其中一个转发，最多转发一次消息。从不同好友的转发，被视为不同的情况。

如果用箭头表示好友关系，下图展示了某个社交网络中消息转发的所有可能情况。 (初始消息是用户1发送的，加粗箭头表示一次消息转发)

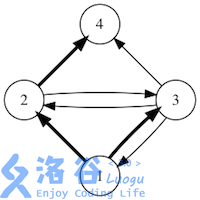
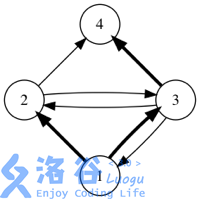
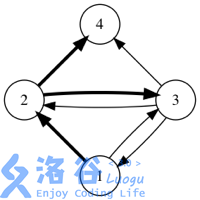
输入输出格式

输入格式：

输入文件第一行，为一个正整数n,表示社交网络中的用户数; 第二行为一个正整数m,表示社交网络中的好友关系数目。

接下来m 行，每行为两个空格分隔的整数 a_iai 和 b_ibi ,表示一组好友关系，即用户 a_iai 可以看到用户 b_ibi 发送的消息。

输出格式：

输出文件共一行，为一条消息所有可能的转发途径的数量，除以10007 所得的余数。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

对于30%的数据， 1≤n≤101≤n≤10

对于100%的数据， 1≤n≤250, 1≤a_i,b_i≤n, 1≤m≤n(n-1)1≤n≤250,1≤ai,bi≤n,1≤m≤n(n−1)

裸的有向图生成树计数问题2333.

不过今天get到了一个新技能(或者说是以前太zz了)，就是在mod数下的高斯消元直接把所有除法变成乘逆元就行了(这不是noip知识点么233为什么以前没想到)，不用什么辗转减。。。。。。

#include<bits/stdc++.h>

#define ll long long

using namespace std;

const int ha=10007;

const int maxn=255;

inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}

inline int ksm(int x,int y){ int an=1; for(;y;y>>=1,x=x*x%ha) if(y&1) an=an*x%ha; return an;}

int n,m,a[maxn][maxn],id[maxn],ans=1,inv,M;

inline void xy(){

	for(int i=2;i<=n;i++){

		if(!a[i][i]){

			ans=ha-ans;

			for(int j=i+1;j<=n;j++) if(a[j][i]){

				for(int k=i;k<=n;k++) swap(a[i][k],a[j][k]);

				break;

			}

		}

		if(!a[i][i]){ ans=0; break;}

		ans=ans*a[i][i]%ha;

		inv=ksm(a[i][i],ha-2);

		for(int j=i+1;j<=n;j++) if(a[j][i]){

			M=inv*a[j][i]%ha;

			for(int k=i;k<=n;k++) a[j][k]=add(a[j][k],ha-a[i][k]*M%ha);

		}

	}

}

int main(){

	int uu,vv;

	scanf("%d%d",&n,&m);

	for(int i=1;i<=m;i++){

		scanf("%d%d",&uu,&vv);

		a[vv][uu]++,id[uu]++;

	}

	for(int i=1;i<=n;i++)

	    for(int j=1;j<=n;j++)

	        if(i==j) a[i][i]=id[i];

	        else a[i][j]=ha-a[i][j];

	xy();

	printf("%d\n",ans);

	return 0;

}