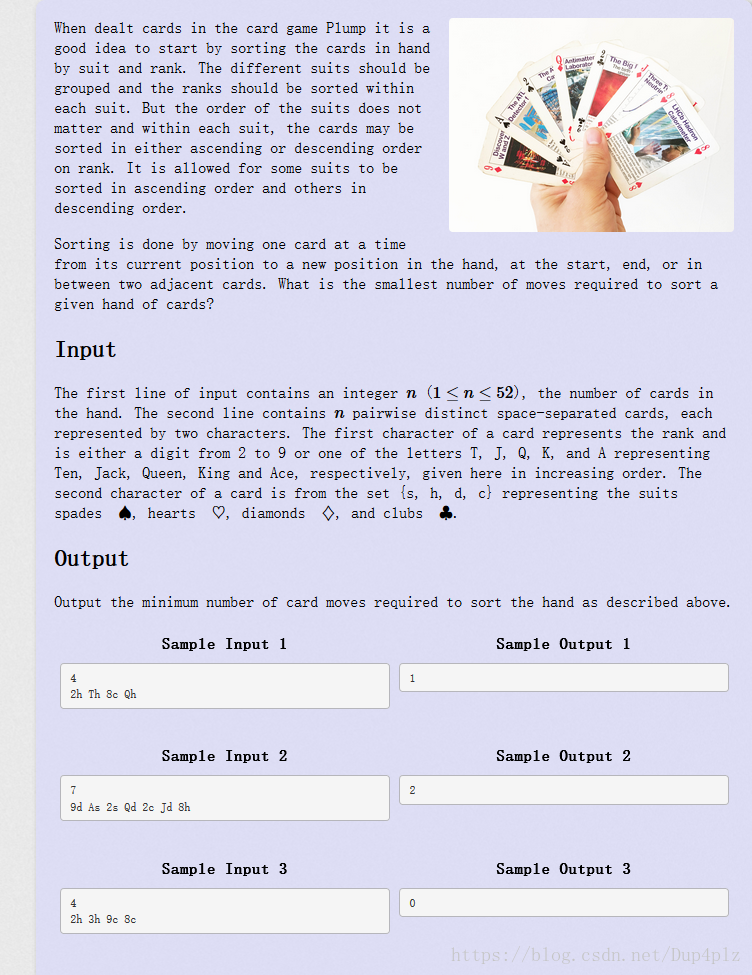
Kattis - cardhand Card Hand Sorting 【暴力枚举】

题意

给出 一个扑克牌的序列 求排成一个“有序”序列 最少的插入次数

有序是这样定义的

同一个花色的 必须放在一起 同一花色中的牌 必须是 升序 或者是 降序

然后 A 是最大的

思路

我们可以枚举一下

一共有四种花色的 就是 4!

每种升序 有 升序 和 降序 就是 2 ^ 4

4 ! * 2 ^ 4 = 384 可以接受

然后次数 怎么求呢 就是 n - LCS(arr)

因为 这不是 交换 来变得 有序 如果是交换来变得有序 就是 求逆序数

插入的话 就将这个序列 求出其 最长上升子列 这个 子列不动 其他元素 依次 插入就可以

然后讲讲 怎么枚举

首先 枚举 花色 就是

我们 将 四种花色 分别与 0 1 2 3 对应起来

然后用一个 数组 arr[4]= {0, 1, 2, 3} 求这个花色的全排列 这就定义了 花色的 先后次序

arr[i] 表示 数字i 对应的花色的优先级是多少

然后 枚举 升序 降序

我们可以用 0-15 这16 个数字的二进制来表示 升序 还是降序

我们可以重新 给它 定义一个 v

降序 就是将 原值 取负数 然后 按 升序排序 实际上 就是 原值的降序排序

比如 0 这个数字 对应四位的二进制数字 是 0000

所以 这个时候 四种花色 都是 升序的 我们可以用花色的优先级 来表示 对应哪位数字

比如 此时 s 花色 对应的 优先级是 0 那么 就是将 0 右移 0 位 再 & 1 就可以判断它对应位 是 1 还是 0

AC代码

#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>

#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair<string, int> psi;
typedef pair<string, string> pss;

const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-30;

const int INF = 0x3f3f3f3f;
const int maxn = 4e5 + 5;
const int MOD = 1e9 + 7;

map <char, int> m;

int color[4] = { 0, 1, 2, 3 };

void init()
{
    m['s'] = 0;   // suit
    m['h'] = 1;
    m['d'] = 2;
    m['c'] = 3;

    for (int i = 2; i <= 9; i++)
    {
        m[i + '0'] = i;
    }
    m['T'] = 10;   // num
    m['J'] = 11;
    m['Q'] = 12;
    m['K'] = 13;
    m['A'] = 14;
}

struct node
{
    int num, suit;
    int v;
    int id;
}q[60];

bool comp(node x, node y)
{
    if (x.suit == y.suit)
        return x.v < y.v;
    else
        return color[x.suit] < color[y.suit];
}

int n;

int LCS(node q[])
{
    int dp[60];
    CLR(dp, 0);
    dp[0] = 1;
    int ans = 1;
    for (int i = 1; i < n; i++)
    {
        dp[i] = 1;
        for (int j = 0; j < i; j++)
        {
            if (q[i].id > q[j].id)
            {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        ans = max(dp[i], ans);
    }
    return ans;
}

int main()
{
    init();
    scanf("%d", &n);
    char s[3];
    for (int i = 0; i < n; i++)
    {
        scanf(" %s", &s);
        q[i].id = i;
        q[i].num = m[s[0]];
        q[i].suit = m[s[1]];
    }
    int ans = INF;
    do
    {
        for (int i = 0; i < 16; i++)
        {
            for (int j = 0; j < n; j++)
            {
                q[j].v = q[j].num * (((i >> color[q[j].suit]) & 1) != 1 ? 1 : -1);
            }
            sort(q, q + n, comp);
            ans = min(ans, n - LCS(q));
        }
    } while (next_permutation(color, color + 4));
    cout << ans << endl;
}