「UVA11181」 Probability|Given（概率

题意翻译

有n个人要去买东西，他们去买东西的概率为p[i]。

现在得知有r个人买了东西，在这种条件下，求每个人买东西的概率。

感谢@s_r_f 提供翻译

题目描述

PDF

输入输出格式

输入格式：

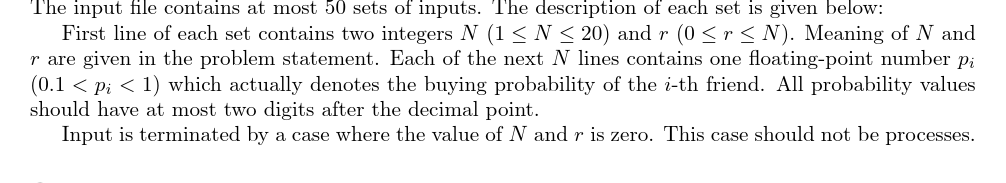
输出格式：

输入输出样例

输入样例#1： 复制

3 2
0.10
0.20
0.30
5 1
0.10
0.10
0.10
0.10
0.10
0 0

输出样例#1： 复制

Case 1:
0.413043
0.739130
0.847826
Case 2:
0.200000
0.200000
0.200000
0.200000
0.200000

题解

这个题面在讲什么鬼话？！！！（气哭

设$E$表示事件＂有$r$个人买了东西＂，$E_i$表示事件＂第$i$个人买了东西＂．

则根据公式，$P(E_i|E)=P({E_i}E)/P(E)$．

问题转化为求$P(E)$和求$P({E_i}E)$．

对于$P(E)$，用$dfs$枚举每个人买了与否．

设$dfs$到了第$i$个人，在它之前的人买与否构成的组合的概率为$now$，

那么若第$i$个人买，概率为$now*p[i]$，否则为$now*(1-p[i])$．

递推下去就好了．

当$dfs$到了第$n$个人，且正好有$r$个人买了，

那么$P(E)+=now$．

然后就是求$P({E_i}E)$了．

其实也差不多，只是多了一个＂第$i$个人必须买＂的限制，所以在$dfs$的时候强制第$i$个人买就行了．

  qwerta
 UVA11181 Probability|Given Accepted
 代码 C++，.79KB
 提交时间 -- ::
 耗时/内存 200ms, 0KB

 #include<iostream>
 #include<cstdio>
 using namespace std;
 double p[];
 double pe;
 int n,r;
 void dfs(int x,int d,double now)
 {
     if(d>r)return;
     if(x==n+)
     {
         if(d==r)
           pe+=now;
         return;
     }
     //mark
     dfs(x+,d+,now*p[x]);
     //dismark
     dfs(x+,d,now*(-p[x]));
     return;
 }
 double pei;
 void dfss(int x,int d,int i,double now)
 {
     if(d>r)return;
     if(x==n+)
     {
         if(d==r)
           pei+=now;
         return;
     }
     if(x==i)
     {dfss(x+,d+,i,now*p[x]);return;}
     //mark
     dfss(x+,d+,i,now*p[x]);
     //dismark
     dfss(x+,d,i,now*(-p[x]));
     return;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     int tim=;
     while(cin>>n>>r)
     {
         if(n==)break;
         printf("Case %d:\n",++tim);
         for(int i=;i<=n;++i)
         cin>>p[i];
         pe=;
         dfs(,,);
         for(int i=;i<=n;++i)
         {
             pei=;
             dfss(,,i,);
             printf("%.6f\n",pei/pe);
         }
     }
     return ;
 }