排列算法汇总（下一个排列，全排列，第K个排列）

一、下一个排列

首先，STL提供了两个用来计算排列组合关系的算法，分别是next_permutation和prev_permutation。

next_permutation(nums.begin(),nums.end());//下一个排列

prev_permutation(nums.begin(),nums.end())//上一个排列

当返回为1时，表示找到了下一全排列；返回0时，表示无下一全排列

1.1下一个排列算法过程

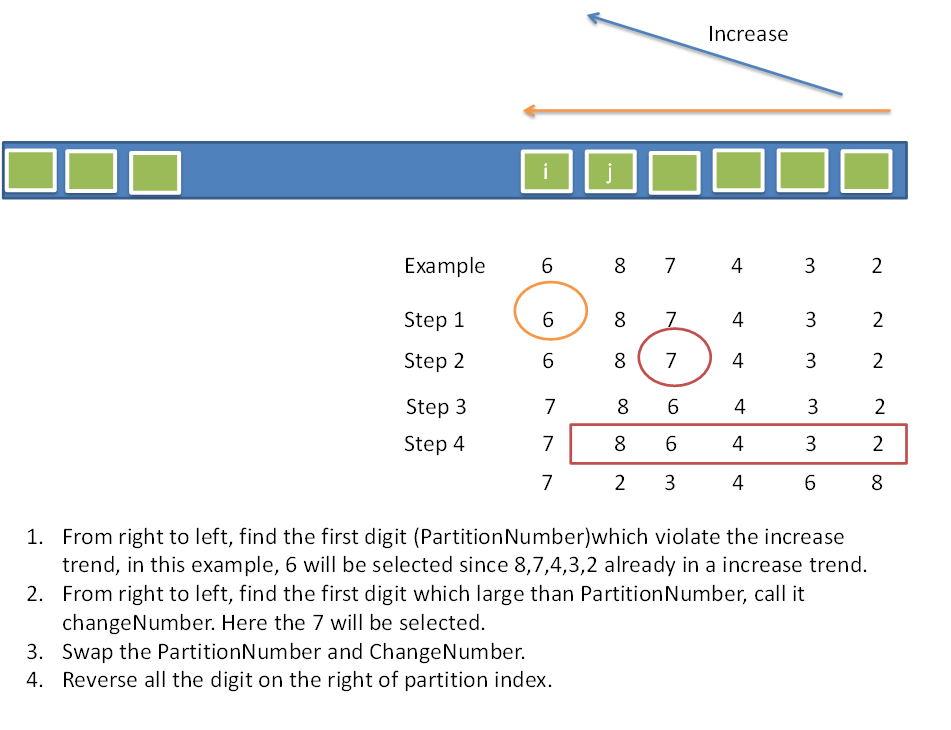
（1）从右到左，找到第一个违反递增趋势的分区数；例如下图的6。

（2）从右到左，找到第一个比分区数大的改变数；例如下图的7。

（3）交换分区数和改变数；例如下图的6和7交换。

（4）颠倒分区数索引的右边所有数字。例如下图的7之后的元素。

1.2 STL源码剖析中的算法过程

（1）首先从最尾端开始往前寻找两个相邻元素，令第一元素为*i,第二元素为*ii,且满足*i<*ii。

（2）找到这样一组相邻元素后，再从最尾端开始往前检验，找出第一个大于*i的元素，令为*j，将i,j元素对调(swap)。

（3）再将ii之后的所有元素颠倒(reverse)排序。

1.3 版本一实现细节（C指针实现）

template<calss BidrectionalIterator>
bool next_permutation(BidrectionalIterator first,BidrectionalIterator last)
{
    if(first == lase) return false; /* 空区间 */
    BidrectionalIterator i = first;
    ++i;
    if(i == last) return false;  /* 只有一个元素 */

    i = last;                    /* i指向尾端 */
    --i;
    for(;;)
    {
        BidrectionalIterator ii = i;
        --i;
        /* 以上锁定一组(两个)相邻元素 */
        if(*i < *ii)           /* 如果前一个元素小于后一个元素 */
        {
            BidrectionalIterator j = last; /* 令j指向尾端 */
            while(!(*i < *--j));     /* 由尾端往前找，直到遇到比*i大的元素 */
            iter_swap(i,j);          /* 交换i,j */
            reverse(ii,last);        /* 将ii之后的元素全部逆序重排 */
            return true;
        }
        if(i == first)       /* 进行至最前面了 */
        {
            reverse(first,last);    /* 全部逆序重排 */
            return false;
        }
    }
}

1.4版本二实现细节（纯STL规范）

 template<typename BidiIt>
  bool next_permutation(BidiIt first,BidiIt last)
  {
        const auto rfirst=reverse_iterator<BidiIt>(last);+++
        const auto rlast=reverse_iterator<BidiIt>(first);

        auto pivot=next(rfirst);

        while( pivot!= rlast && *pivot >= *prev(pivot))
              ++pivot;//直到找出第一个违反递增趋势的分区数，此时，pivot指向分区数;

       if(pivot == rlast)
      {
              reverse(rfirst,rlast);//如果此序列为递减系列，则下一个排序为颠倒整个序列;
              return false;
      }

       auto change=find_if(rfirst,rlast,bindlst(less<int>(),*pivot));//从右到左，找到第一个大于分区数的数，并赋给change;

       swep(*change,*pivot);//交换分区数与改变数;

       reverse(rfirst,pivot);//将分区数之后的序列颠倒;

       return true;
 }

1.5 前一个排列（prev_permutation）

与next_permutation类似，STL也提供一个版本：

 int prev_permutation(int *begin, int *end)
 {
     int *i=begin, *j, *k;
     if (i==end || ++i==end) return ;   // 0 or 1 element, no prev permutation
     for (i=end-; i!=begin;) {
         j = i--;    // find last decreasing pair (i,j)
         if (!(*i > *j)) continue;
         // find last k which less than i,
         for (k=end; !(*i > *(--k)););
         iter_swap(i,k);
         // now the range [j,end) is in ascending order
         reverse(j,end);
         return ;
     }
     // current is in ascending order
     reverse(begin,end);
     return ;
 }

二、全排列

1.1 利用next_permutation求全排列

对初始序列依次求下一个排列，直到没有下一个序列为止。

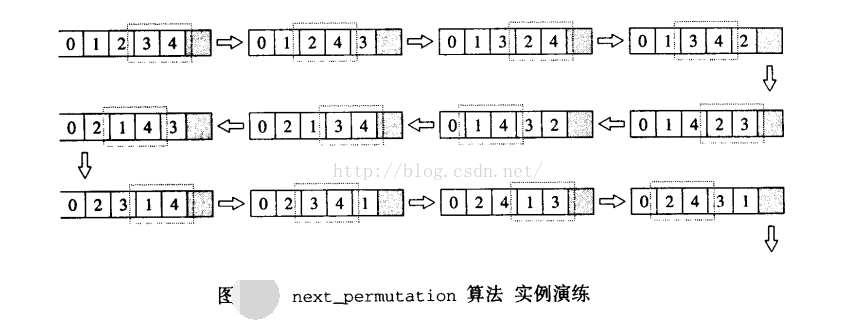
举个实例，假设有序列{0,1,2,3,4}，下图便是套用上述演算法则，一步一步获得“下一个”排列组合。图中只框出那符合“一元素为*i,第二元素为*ii,且满足*i<*ii ”的相邻两元素，至于寻找适当的j、对调、逆转等操作并未显示出。

代码如下：

    vector<vector<int>> permute(vector<int>& nums) {
        vector<int>temp;
        vector<vector<int>>result;
        sort(nums.begin(),nums.end());
        do
        {
            temp.clear();
            for(int i=;i<nums.size();i++)
                temp.push_back(nums[i]);
            result.push_back(temp);
        }while(next_permutation(nums.begin(),nums.end()));//do while循环最适合，因为先要打印出初始序列
        return result;
    }

1.2 利用深度优先搜索（DFS）求解，以后待更新。

三、第K个排列

简单的，可以用暴力枚举法，调用k-1次next_permutation()(注意一定是k-1次)

代码如下：

     string getPermutation(int n, int k) {
         string str(n,'');
         for(int i=;i<n;i++)
             str[i]+=i+;
         for(int i=;i<k-;i++)
             next_permutation(str.begin(),str.end());
         return str;
     }