Codeforces Round#409/VK-Cup 2017 Round2

来自FallDream的博客，未经允许，请勿转载，谢谢。

---

和ditoly组队打VK-Cup，起了个名字叫Vegetable Chicken(意思显然)，然后昨天我做AB他切C

很不幸的是.....我写的两题都挂了......坑队友了...A被疯狂卡精度  B简单计算几何瞎写挂了  GG 滚去外卡赛

A.Voltage Keepsake

你有n个东西，每个东西每秒钟消耗ai的能源，初始有bi的能源。你还有一个充电器，每秒钟可以充p的能源，问最多多久之后才有东西爆零。n<=100000

直接二分呗。然后记得直接把$\sum{ai}\leqslant p$的直接判掉，不然被疯狂卡精度，longdouble过不去，但是float128可过(10倍常数左右)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#include<map>
#define eps 1e-6
#define MN 100000
#define ll long long
#define ld long double
using namespace std;
inline int read()
{
    int x = ,f = ; char ch = getchar();
    while(ch < '' || ch > ''){if(ch == '-') f = ;ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return f?x:-x;
}

int n;
ld a[MN+],b[MN+],p,tot;

int main()
{
    n=read();p=read();
    for(int i=;i<=n;i++)a[i]=read(),b[i]=read(),tot+=a[i];
    if(tot<=p)return *puts("-1");
    ld l=,r=1e18,mid,sum=;
    for(int j=;j<=;j++)
    {
        mid=(l+r)/2.0;sum=;
        for(int i=;i<=n;i++)
            sum+=max((ld),(a[i]*mid-b[i])/p);
        if(sum<mid+eps) l=mid;
        else r=mid;
    }
    if(r+eps>=(ld)1e17) return *puts("-1");
    printf("%0.6lf\n",(double)(l+r)/2.0);
    return ;
}

B. Volatile Kite
给定一个凸多边形，求一个最大的D，每个点无论在距离D里面怎么移动，都还是凸多边形. n<=1000

发现题目是求一个点到两点连线距离的最小值的一半，只要判相邻的三个点就行了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#include<map>
#define eps 1e-8
#define MN 1000
#define ll long long
using namespace std;
inline int read()
{
    int x = ,f = ; char ch = getchar();
    while(ch < '' || ch > ''){if(ch == '-') f = ;ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return f?x:-x;
}
inline double sqr(double x){return x*x;}
struct P
{
    double x,y;
    P(double _x=,double _y=):x(_x),y(_y){}
    double operator^(P b){return fabs(x*b.y-b.x*y);}
    P operator-(P b){return P(x-b.x,y-b.y);}
    friend double dis(P a,P b){return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));}
}p[MN+];

int n;
double ans=1e18;

int main()
{
    n=read();
    for(int i=;i<=n;i++) p[i].x=read(),p[i].y=read();
    for(int i=;i<n;i++) ans=min(ans,dis(p[i],p[i+])/2.0);
    ans=min(ans,dis(p[n],p[])/2.0);
    p[n+]=p[];p[n+]=p[];
    for(int i=;i<=n;i++)
        ans=min(ans,((p[i]-p[i+])^(p[i+]-p[i+]))/dis(p[i],p[i+])/);
    printf("%0.7lf\n",ans);
    return ;
}

C.给定n个0-m-1的数字和m，你要构造一个尽可能长的数列，满足前缀积互不相同，且n个数都没有出现。n<=m<=200000

裴蜀定理，把每一个数字和m求gcd然后扔在一起，然后每个gcd都可以向它的倍数转移，dp求一个最长路径，最后用exgcd求一下方程系数输出就行了。

#include<iostream>
#include<cstdio>
#include<vector>
#define MN 200000
using namespace std;
inline int read()
{
    int x =  , f = ; char ch = getchar();
    while(ch < '' || ch > ''){ if(ch == '-') f = -;  ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return x * f;
}

int  n , m , from , ans =  , f[MN + ] , last =  , ne[MN + ];
bool b[MN + ];
vector<int> v[MN + ];
inline int gcd(int x,int y){return !y ? x :gcd(y , x % y);}

int exgcd(int a , int b , int&x , int&y)
{
    if(!b) {x =  , y = ; return a;}
    int c = exgcd(b , a % b , x , y);
    int t = x; x = y; y = t - (a / b) * x;
    return c;
}

void solve(int x)
{
    if(ne[x]) solve(ne[x]);
    int X = , Y =  , Z;
    for(int i =  ; i < v[x].size() ; ++i)
        Z = exgcd(last , m , X , Y) , printf("%d ",(1LL * X * v[x][i] / Z % m + m) % m) , last = v[x][i];
}

int main()
{
    n = read(); m = read();
    for(int i =  ; i <= n ; ++i) b[read()] = ;
    for(int i =  ; i < m ; ++i) if(!b[i]) v[gcd(i , m)].push_back(i);
    for(int i =  ; i < m ; ++i)
    {
        if((f[i] += v[i].size()) > ans) ans = f[i] , from = i;
        for(int j = i <<  ; j < m ; j += i)
            if(f[i] > f[j]) f[j] = f[i] , ne[j] = i;
    }
    printf("%d\n", ans + !b[]);
    solve(from);
    if(!b[]) puts("");
    return ;
}

D.Varying Kibibits

定义f(s1,s2...sn)的每一位是这n个数里面那一位的最小值  求

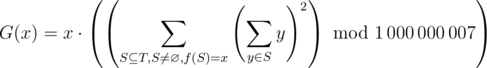
就是对于每一个f(x)的值等于x的子序列si，计算它的和的平方的和乘以x.

给定n个数，求G(1)^G(2)^...^G(n)  n<=10^6 数字在[0,10^6-1]

题解：枚举x，如果直接算等于x的，显然不好做，考虑容斥原理，计算每一位都大等于x的每一位的答案。这样我们只要对于一个集合能够求出它的子集的和的平方和就行了。

比如只有两个数字a,b 答案是$(a^{2}+b^{2})+(a+b)^{2}$

如果有三个数字abc,答案是$2(a^{2}+b^{2}+c^{2})+2(a+b+c)^2$

......

然后经过乱拆之后一番找规律，发现如果有k个数字，答案是2^(k-2)乘以它们的平方和加上和的平方，k比较小的时候特判一下。所以我们对于每一个数，维护大等于它的数字的 平方和 ， 和 ， 数字个数  就可以算出答案了。

转移和计算答案都用容斥原理，2的次方可以预处理，复杂度$O(2^{6}*10^{6})$，自带大常数，我上fread卡了一会儿常数才过去。

代码有点丑

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#include<map>
#define MN 1000000
#define ll long long
#define mod 1000000007
char B[<<],*S=B;
#define getchar() (*S++)
using namespace std;
inline int read()
{
    int x = ,f = ; char ch = getchar();
    while(ch < '' || ch > ''){if(ch == '-') f = ;ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return f?x:-x;
}

int n,num[MN+],sq[MN+],sum[MN+],a[MN+],C,D,pw[],X,p[MN+];
ll res=,ans;
inline void R(int&x,int y){x+=y;(x>=mod)?x-=mod:;x<?x+=mod:;}
void dfs(int x,int now,int k,int l)
{
    if(x>)
    {
        if(l!=X&&num[l])
        {
            R(num[X],k*num[l]);
            R(sq[X],k*sq[l]);
            R(sum[X],k*sum[l]);
        }
        return;
    }
    int la=now%;now/=;
    dfs(x+,now,k,l+la*pw[x]);
    if(la<) dfs(x+,now,-k,l+(la+)*pw[x]);
}

inline int Sqr(int x){return 1LL*x*x%mod;}
void solve(int x,int now,int k,int l)
{
    if(x>)
    {
        if(num[l])
        {
            if(k==-) k=mod-;
            if(num[l]==) ans=(ans+1LL*k*Sqr(sum[l]))%mod;
            else
            {
                int times=p[num[l]-2];
                ans=(ans+1LL*k*times%mod*(1LL*Sqr(sum[l])+sq[l])%mod)%mod;
            }
        }
        return;
    }
    int la=now%;now/=;
    solve(x+,now,k,l+la*pw[x]);
    if(la<) solve(x+,now,-k,l+(la+)*pw[x]);
}

inline int U(int x){return x>=mod?x-=mod:x;}

int main()
{
    fread(B,,<<,stdin);
    n=read();pw[]=p[]=;
    for(int i=;i<=;i++) p[i]=U(p[i-]<<);
    for(int i=;i<=;i++)pw[i]=pw[i-]*;
    for(int i=;i<=n;i++)
        ++num[a[i]=read()],sq[a[i]]=(sq[a[i]]+1LL*a[i]*a[i])%mod,(sum[a[i]]+=a[i])%=mod;
    for(X=;~X;--X) dfs(,X,-,);
    for(X=;X;--X)
    {
        ans=;solve(,X,,);
        res=res^(1LL*ans*X);
    }
    cout<<res;
    return ;
}