TopCoder SRM 558 Div 1 - Problem 1000 SurroundingGame

传送门：https://284914869.github.io/AEoj/558.html

题目简述 

一个人在一个n * m棋盘上玩游戏，想要占领一个格子有两个方法：

在这个格子放一个棋子。
  这个格子周围(四联通)的格子中**都有棋子**。

在(i, j)中放棋子需要花费cost[i][j]，占领(i, j)能获得benefit[i][j]。求一种放置棋子的方法，使得总收益(收益 - 花费)最大。

2<=n,m<=20

分析

一眼看上去，

状压？

我是不是dp学傻了。。根本想不出

网络流？

嗯，此题是一道非常套路的网络流练习题。

如果想不到对棋盘进行黑白染色，就GG了。

所以套路之一，你要对棋盘进行黑白染色，黑点放一边，白点放一边。

感受一下，肯定是建个图，连一些收益边、花费边，跑一遍最大流来求最小割之类的。

套路之二，引用一段zzx的话：“

要验证你建出来的图是否正确也很容易，

只要看看当你选择保留某条收益边的时候，会要割掉哪些边。

假如需要割边的情况和题目要求一致，这个图就建对了。”

如何建边？

我来讲一下我的心路历程。。。（毕竟我是一个网络流萌新，这应该是我做过的第5道网络流题目）。

首先，

我们先把所有收益算上，不算任何花费。这显然是不合法的，

所以建的图要满足，当收益与花费不合法的情况下，还能继续找到从源点到汇点的一条流量>0的路径。

这时需要割去一些边（增加花费，或减少收益），使得收益与花费合法，且割去的边权值和最小（即总收益最大），这就是最小割。

对于花费边，

某一个格子，得到它的收益，一种情况是用该格子的花费，还有一种情况是用与它相邻的四个格子的花费。

由于已经进行黑白染色，该格子与相邻四个格子的颜色不同。

那么可以脑补出下图：

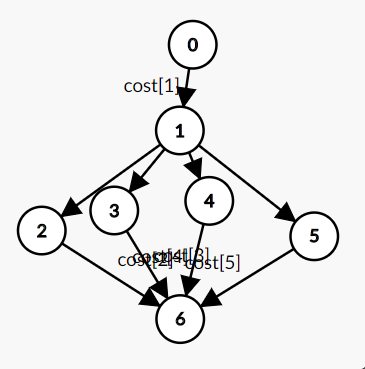
图中0是源点，6是汇点。

左图中，可以选择割0-1，即用1的花费，或选择割2-6，3-6，4-6，5-6，即用相邻四个格子的花费。

考虑这样还没完，因为你也可以选择放弃这个格子的收益。

同时我们又不能再加一条收益边与上图串联，

因为放弃这个格子的收益，代表着相邻的格子的收益必须要靠它自己的花费。所以简单的串联很显然是不对的。

所以我们考虑，割掉1的收益边之后，左图不存在流量>0的路，但对右图没有影响。

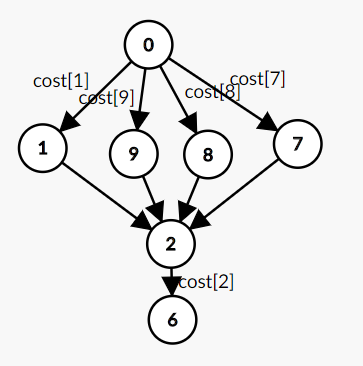
于是诞生了下图的连边方式：

简单地说，就是把所有的点都拆成两个点，两个点之间连收益边。

如图中一号收益边，割去之后，不存在经过 1‘ 到汇点的路，但依然存在经过1,9,8,7再经过2再到汇点的路。这样就合法了。

题外话：

一开始以为输入的字符，A-Z代表10~35，a-z代表36-61，写完代码之后发现一直wa，过了好久发现自己搞反了

之后又把数组开小了。。。。真难过

代码：

 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 #define _CLASSNAME_ SurroundingGame
 #define _METHODNAME_ maxScore
 #define _RC_ int
 #define _METHODPARMS_ vector <string> cost, vector <string> benefit
 #define ref(i,x,y)for(int i=x;i<=y;++i)
 #define def(i,x,y)for(int i=x;i>=y;--i)
 const int inf = (int)1e9;
 int n, m, op, ed, w1[][], w2[][];
 int cnt, head[], d[][] = { {,},{,},{-,},{,-} };
 struct edge {
     int to, next, s;
     edge() {}
     edge(int a, int b, int c) : to(a), next(b), s(c) {}
 }e[];
 int p(int x, int y, int s) {
     return s*n*m + (x - )*m + y + ;
 }
 void Add(int x, int y, int s) {
     //if (x > ed || y > ed || x<1||y<1) { cout << "err" << endl; }
     //cout << x << " " << y << " " << s << endl;
     e[++cnt] = edge(y, head[x], s); head[x] = cnt;
     e[++cnt] = edge(x, head[y], ); head[y] = cnt;
 }
 void build() {
     memset(head, , sizeof head);
     memset(e, , sizeof e);
     cnt = ;
     op = p(, , ) - , ed = p(n, m, ) + ;
     ref(i, , n) ref(j, , m) {
         if ((i & ) == (j & )) {
             Add(op, p(i, j, ), w1[i][j]);
             Add(p(i, j, ), p(i, j, ), w2[i][j]);
             ref(k, , ) {
                 int I = i + d[k][], J = j + d[k][];
                 if (I< || J< || I>n || J>m)continue;
                 Add(p(i, j, ), p(I, J, ), inf);
             }
         }
         else {
             Add(p(i, j, ), ed, w1[i][j]);
             Add(p(i, j, ), p(i, j, ), w2[i][j]);
             ref(k, , ) {
                 int I = i + d[k][], J = j + d[k][];
                 if (I< || J< || I>n || J>m)continue;
                 Add(p(I, J, ), p(i, j, ), inf);
             }
         }
     }
 }
 int ans, flow[], pre[]; bool vis[];
 void work() {
     while () {
         //cout << ans << endl;
         memset(flow, , sizeof flow);
         memset(pre, , sizeof pre);
         memset(vis, , sizeof vis);
         flow[op] = inf;
         int o, f;
         while () {
             o = ; f = ;
             ref(i, op, ed)if (!vis[i] && flow[i] > f)
                 f = flow[i], o = i;
             if (o ==  || o == ed)break;
             vis[o] = ;
             for (int i = head[o]; i; i = e[i].next) {
                 int v = e[i].to; if (vis[v])continue;
                 int s = min(f, e[i].s); if (s <= flow[v])continue;
                 flow[v] = s; pre[v] = i;
                 //if (v > ed) { cout << "err" << endl; }
             }
         }
         if (o == )break;
         for (; o != op; o = e[pre[o] ^ ].to) {
             e[pre[o]].s -= f; e[pre[o] ^ ].s += f;
         }
         ans -= f;
     }
     //cout << ans << endl;
 }
 int chd(char c) {
     if (c >= ''&&c <= '')return c - '';
     if (c >= 'a'&&c <= 'z')return c - 'a' + ;
     if (c >= 'A'&&c <= 'Z')return c - 'A' + ;
 }
 class _CLASSNAME_ {
 public:
     _RC_ _METHODNAME_(_METHODPARMS_) {
         memset(w1, , sizeof w1);
         memset(w2, , sizeof w2);
         ans = ;
         n = cost.size();
         m = cost[].size();
         ref(i, , n)ref(j, , m) {
             w1[i][j] = chd(cost[i - ][j - ]);
             w2[i][j] = chd(benefit[i - ][j - ]);
             ans += w2[i][j];
         }
         build();
         work();
         return _RC_(ans);
     }

     // BEGIN CUT HERE
 public:
     void run_test(int Case) { if ((Case == -) || (Case == )) test_case_0(); if ((Case == -) || (Case == )) test_case_1(); if ((Case == -) || (Case == )) test_case_2(); if ((Case == -) || (Case == )) test_case_3(); if ((Case == -) || (Case == )) test_case_4(); if ((Case == -) || (Case == )) test_case_5();}
 private:
     template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '\"' << *iter << "\","; os << " }"; return os.str(); }
     void verify_case(int Case, const int &Expected, const int &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << "\tExpected: \"" << Expected << '\"' << endl; cerr << "\tReceived: \"" << Received << '\"' << endl; } }
     void test_case_0() { string Arr0[] = { "","" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); string Arr1[] = { "","" }; vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1)); }
     void test_case_1() { string Arr0[] = { "ZZ","ZZ" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); string Arr1[] = { "","" }; vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1)); }
     void test_case_2() { string Arr0[] = { "XXX","XXX","XXX" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); string Arr1[] = { "aaa","aZa","aaa" }; vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1)); }
     void test_case_3() { string Arr0[] = { "asam","atik" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); string Arr1[] = { "123A","45BC" }; vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1)); }
     void test_case_4() {
         string Arr0[] = { "IIIIIIII",
             "IIWWWWII",
             "IIWIIIII",
             "IIWIIIII",
             "IIWWWWII",
             "IIIIIWII",
             "IIIIIWII",
             "IIWWWWII",
             "IIIIIIII" }
         ; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[]))); string Arr1[] = { "IIIIIIII",
             "II0000II",
             "II0II0II",
             "II0II0II",
             "II0000II",
             "II0II0II",
             "II0II0II",
             "II0000II",
             "IIIIIIII" }
         ; vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[]))); int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1));
     }
     void test_case_5() {
         string Arr0[] = { "ej8i1lj87i54767cbkla",
             "7m4l31ehe4c337k9lee6",
             "4h24Z91ab8a649dacmc4",
             "0f0631g78g8461jk8i4c",
             "baf21g6g5a6c75Z8a3ke",
             "7f957i0ib888ed1k06ga",
             "j2cb87d949ghkifg3m1i",
             "fi53Zee4ij8ded796l6b",
             "k015e95m415gbgkml29m",
             "aidlk9kmj2lkdbZ4digm",
             "he67f0clim758be5a69a",
             "03i54c218elje2kbl5im",
             "djjjZb36l124012c7fdb",
             "jhe38eh2i1fi3l061hk6",
             "216i59211a67g3Z0934c",
             "db5kbmjm1e3be4l8bml0",
             "h22ee7gm20j82mmg6eh0",
             "89aiY4c7a1cg41d1ahck",
             "lcma6i2171kjk7l9h65l",
             "lmhif2m96098g6Z84ka3" }; vector <string> Arg0(Arr0, Arr0 + (sizeof(Arr0) / sizeof(Arr0[])));
         string Arr1[] = { "a97e5100a1b45d9ae663", "897696a9c2fc8fe803ea", "03te33c97c81af5b9a26", "3743f85dd2b87b1cd20f", "3dl3a00f706b4217f220", "5a71bdadpf4bc48db593", "02l52900cca45f348dac", "cc3dd16b08c837142ada", "A70e94239c87af935b50", "f0be492c0bda3b0b4062", "050838039967e420cc98", "eed15ec303858d472304", "090b0607f91515ef4537", "cae6ebb4096e73429695", "0cH554009df2a470cd15", "36c976d9096f5c4a4c40", "06690c3b3c585207c46d", "08779dd1a5131a60122e", "D7099feb596918e9324e", "ddd3785103238eac8ef8" };
         vector <string> Arg1(Arr1, Arr1 + (sizeof(Arr1) / sizeof(Arr1[])));
         int Arg2 = ; verify_case(, Arg2, maxScore(Arg0, Arg1));
     }

     // END CUT HERE
 };
 // BEGIN CUT HERE
 int main() {
     cout << "This is SurroundingGame" << endl;
     SurroundingGame ___test;
     ___test.run_test(-);
     getchar();
     return ;
 }
 // END CUT HERE