Nonlinear Component Analysis as a Kernel Eigenvalue Problem

引
kernel PCA
代码

Scholkopf B, Smola A J, Muller K, et al. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319.

引

普通的PCA将下式进行特征分解（用论文的话讲就是对角化）：

\[C = \frac{1}{M} \sum \limits_{j=1}^M x_j x_j^T
\]

其中$x_j \in \mathbb{R}^{N}, j = 1, \ldots, M$，且$\sum \limits_{j=1}^M x_j = 0$(中心化)。

而kernel PCA试图通过一个非线性函数：

\[\Phi:\mathbb{R}^N \rightarrow F, x \rightarrow X
\]

其中$F$是一个高维空间（甚至是无限维)。

所以我们要解决这么一个问题：

\[\bar{C} = \frac{1}{M} \sum_{j=1}^M \Phi (x_j) \Phi(x_j)^T
\]

其实我们面对的第一个问题不是维度的问题而是$\Phi$的选择或者说构造。我们为什么要把数据映射到高维的空间？因为当前数据的结构（或者说分布）并不理想。

比如满足$(x-1)^2+(y-1)^2=4$的点，我们可以扩充到高维空间$(x^2, x, y, y^2)$，在高维空间是线性的（虽然这个例子用在kernel SVM 比较好）。

因为$\Phi(\cdot)$的构造蛮麻烦的，即便有一些先验知识。我们来看一种比较简单的泛用的映射：

\[(x_1, x_2, x_3) \rightarrow (x_1^3, x_2^3, x_3^3, x_1^2x_2,x_1^2x_3,x_1x_2^2,x_1x_3^2,x_2^2x_3,x_2x_3^2,x_1x_2x_3)
\]

这种样子的映射，很容易把维度扩充到很大很大，这个时候求解特征问题会变得很麻烦。

kernel PCA

假设$\sum \limits_{i=1}^M \Phi(x_i)=0$(如何保证这个性质的成立在最后讲，注意即便$\sum \limits_{i=1}^M x_i = 0$，$\sum \limits_{i=1}^M \Phi(x_i)=0$也不一定成立)。

假设我们找到了$\bar{C}$的特征向量$V \ne 0$:

\[\bar{C}V = \lambda V
\]

因为$V$是$\Phi(x_i),i=1,\ldots, M$的线性组合（这个容易证明），所以，$V$可以由下式表示：

\[V = \sum \limits_{i=1}^M \alpha_i \Phi(x_i)
\]

所以：

\[\lambda V^T \Phi(x_j) = V^T\bar{C} \Phi(x_j), \quad for \: all \: j=1,\ldots, M
\]

等价于(记$\Phi = [\Phi(x_1), \ldots, \Phi(x_M)]$)：

\[\begin{array}{ll}
\lambda \sum \limits_{i=1}^M \alpha_i (\Phi^T(x_i)\Phi(x_j))
&= \lambda \{ \Phi^T \Phi(x_j)\} ^T \alpha \\
& =\frac{1}{M} \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi \Phi^T \Phi(x_j) \\
& = \frac{1}{M} \{\Phi^T \Phi \Phi^T \Phi(x_j)\}^T \alpha
\end{array}
\]

对于$j=1,\ldots, M$均成立，其中$\alpha = [\alpha_1, \ldots, \alpha_M]^T$。

等价于：

\[M \lambda \Phi^T \Phi \alpha = \Phi^T \Phi \Phi^T \Phi \alpha
\]

令$K = \Phi^T \Phi$，那么可写作：

\[M \lambda K \alpha = K^2\alpha
\]

其中$K_{ij} = \Phi^T(x_i) \Phi(x_j)$

所以，我们可以通过下式来求解$\alpha$:

\[M\lambda \alpha = K \alpha
\]

即$\alpha$是$K$的特征向量(注意，当$\alpha$为特征向量的时候是一定符合$M \lambda K \alpha = K^2\alpha$的，反之也是的，即二者是等价的)。

假设$\lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_M$对应$\alpha^1, \ldots, \alpha^M$，那么相应的$V$也算是求出来了。

需要注意的是，$\|\alpha\|$往往不为1，因为我们希望$\|V\|=1$，所以：

\[V^TV = \alpha^T K \alpha = \lambda \|\alpha\|^2 = 1
\]

所以$\|\alpha\| = \frac{1}{\sqrt{\lambda}}$

PCA当然需要求主成分，假设有一个新的样本$x$，我们需要求：

\[\Phi(x)^TV = \Phi^T(x) \Phi \alpha = \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi(x)
\]

注意，我们只需要计算$\Phi^T(x_i) \Phi(x)$。

现在回到kernel PCA 上的关键kernel上。注意到，无论是K，还是最后计算主成分，我们都只需要计算$\Phi^T(x)\Phi(y)$就可以了，所以如果我们能够找到一个函数$k(x,y)$来替代就不必显示将$x$映射到$\Phi(x)$了，这就能够避免了$\Phi(\cdot)$的选择问题和计算问题。

kernel 的选择

显然，PCA的$\lambda \ge 0$，所以我们也必须保证$K$为半正定矩阵，相应的核函数$k$称为正定核，Mercer定理有相应的构建。

也有现成的正定核：

多项式核

\[k(x, y) = (x^Ty + 1)^d
\]

论文中是$(x^Ty)^d$

高斯核函数

\[k(x, y) = \exp \{\ -\frac{\|x-y\|^2}{2\sigma^2}\}
\]

性质

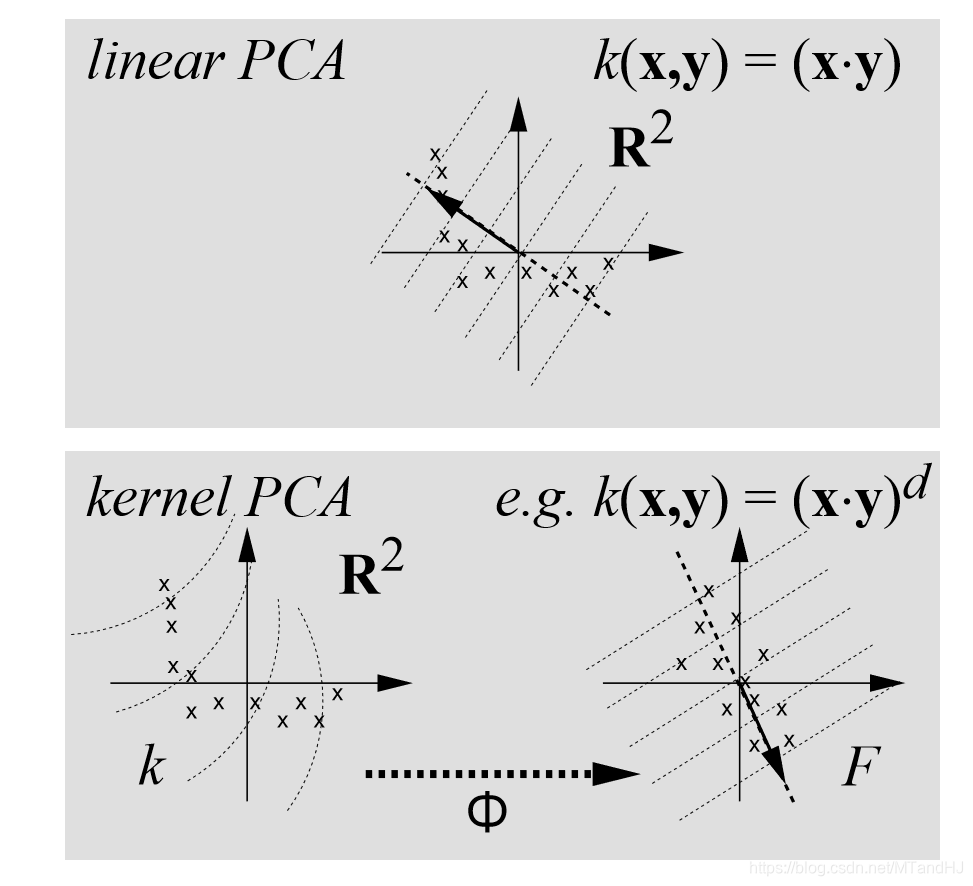
论文用上面的一个例子来说明，kernel PCA可能更准确地抓住数据的结构。

kernel PCA具有普通PCA的性质，良好的逼近（从方差角度），以及拥有最多的互信息等等。并且，如果$k(x, y) = k(x^Hy)$，那么kernel PCA还具有酉不变性。

因为普通的PCA处理的是一个$N \times N$的协方差矩阵，所以，至多获得$N$个载荷向量，而kernel PCA至多获得$M$个载荷向量(特征值非零)。所以，kernel PCA有望比普通PCA更加精准。

一些问题

中心化

PCA处理的是协方差矩阵，正如我们最开始所假设的，$\sum \limits_{i=1}^{M} \Phi(x_i)=0$,即中心化。因为$\Phi(\cdot)$并不是线性函数，所以，即便$\sum \limits_{i=1}^M x_i = 0$也不能保证$\sum \limits_{i=1}^{M} \Phi(x_i)=0$，不过有别的方法处理。

令

\[\tilde{\Phi}(x_i) = \Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k) \\
\tilde{K}_{ij} = \tilde{\Phi}^T(x_i) \Phi(x_j) \\
1_{M} = \{1\}_{ij}^{M \times M}
\]

可以得到：

\[\begin{array}{ll}
\tilde{K}_{ij} &= \tilde{\Phi}^T(x_i) \Phi(x_j) \\
&= \big(\Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big)^T \big(\Phi(x_j) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big) \\
&= K_{ij} - \frac{1}{M} \sum \limits_{k=1}^M K_{kj} - \frac{1}{M} \sum \limits_{k=1}^M K_{ik} + \frac{1}{M^2} \sum \limits \limits_{m,n=1}^M K_{mn} \\
&= (K - 1_MK - K1_M + 1_MK1_M)_{ij}
\end{array}
\]

于是，我们通过$K$可以构造出$\tilde{K}$。只需再求解$\tilde{K}\tilde{\alpha} = M \lambda \tilde{\alpha}$即可。

恢复

我们知道，根据PCA选出的载荷向量以及主成分，我们能够恢复出原数据（或者近似，如果我们只选取了部分载荷向量）。对于kernel PCA，比较困难，因为我们并没有显式构造$\Phi(\cdot)$，也就没法显式找到$V$，更何况，有时候我们高维空间找到$V$在原空间中并不存在原像。

或许，我们可以通过：

\[\min \limits_{x} \quad \|\Phi(x) - \Phi(\hat{x})\|^2
\]

来求解，注意到，上式也只和核函数$k(x,y)$有关。

代码



import numpy as np

class KernelPCA:

    def __init__(self, data, kernel=1, pra=3):

        self.__n, self.__d = data.shape

        self.__data = np.array(data, dtype=float)

        self.kernel = self.kernels(kernel, pra)

        self.__K = self.center()

    @property

    def shape(self):

        return self.__n, self.__d

    @property

    def data(self):

        return self.data

    @property

    def K(self):

        return self.__K

    @property

    def alpha(self):

        return self.__alpha

    @property

    def eigenvalue(self):

        return self.__value

    def kernels(self, label, pra):

        """

        数据是一维的时候可能有Bug

        :param label: 1:多项式;2:exp

        :param pra:1: d; 2: sigma

        :return: 函数 或报错

        """

        if label is 1:

            return lambda x, y: (x @ y) ** pra

        elif label is 2:

            return lambda x, y: \

                np.exp(-(x-y) @ (x-y) / (2 * pra ** 2))

        else:

            raise TypeError("No such kernel...")

    def center(self):

        """中心化"""

        oldK = np.zeros((self.__n, self.__n), dtype=float)

        one_n = np.ones((self.__n, self.__n), dtype=float)

        for i in range(self.__n):

            for j in range(i, self.__n):

                x = self.__data[i]

                y = self.__data[j]

                oldK[i, j] = oldK[j, i] = self.kernel(x, y)

        return oldK - 2 * one_n @ oldK + one_n @ oldK @ one_n

    def processing(self):

        """实际上就是K的特征分解,再对alpha的大小进行一下调整"""

        value, alpha = np.linalg.eig(self.__K)

        index = value > 0

        value = value[index]

        alpha = alpha[:, index] * (1 / np.sqrt(value))

        self.__alpha = alpha

        self.__value = value / self.__n

    def score(self, x):

        """来了一个新的样本，我们进行得分"""

        k = np.zeros(self.__n)

        for i in range(self.__n):

            y = self.__data[i]

            k[i] = self.kernel(x, y)

        return k @ self.__alpha

"""

import matplotlib.pyplot as plt

x = np.linspace(-1, 1, 100)

y = x ** 2 + [np.random.randn() * 0.1 for i in range(100)]

data = np.array([x, y]).T

test = KernelPCA(data, pra=1)

test.processing()

print(test.alpha.shape)

print(test.alpha[:, 0])

"""